4. Поясніть метод моделювання неперервних випадкових величин методом режекції. Наведіть приклад.

Метод Неймана, так же как метод обратной функции, является методом, позволяющим получить значения случайной величины в соответствии с заданным законом распределения. Этот метод является достаточно универсальным и он применим для моделирования всех случайных величин, значения которых не выходят за пределы ограниченного интервала (a,b.)

Из датчика равномерно распределенных в интервале (0, 1) случайных чисел независимо выбираются пары чисел , из которых формируются преобразованные пары , ,  где (a, b) — интервал возможных значений случайной величины  с заданной функцией плотности ;  — максимальное значение функции . В качестве реализации случайной величины берется число  из тех пар ,  которых выполняется неравенство

.                                    

Пары, не удовлетворяющие неравенству, выбрасываются.

4. Як визначити, чи належіть розподіл випадкової величини, який одержан експериментально, теоретичному розподілу?

Належність розподілу випадкової величини, одежраного експериментально, теоретичному розподілу визначається за допомогою застосування одного з критеріїв для перевірки гіпотези про приналежність деякої вибірки теоретичному закону розподілу.

Найпопулярнішим з цих методів є Критерій згоди Пірсона, або Критерій згоди (Хі-квадрат).

Хі -квадрат передбачає розбиття вибірки на інтервали та визначення частоти nj для кожного з інтервалів. Для зручності розрахування інтервали вибирают однакової довжини.

Статистикою критерія пірсона слугує величина

де p_j - це вірогідність потрапляння випадкової величини у j-й інтервал, розрахована у відповідності з гіпотетичним законом розподілу F(x). При розрахунку вірогідності p_j треба звернути увагу на те, що ліва границя першого інтервалу і права границя останнього повинні співпадати з границями області можливих значень випадкової величини.

Далі, отримавши значення x² , його порівнюють з значенням x²_a, знайденим по спеціальній таблиці для вибраного рівня значущості a та числа степенів свободи k = e₁ - m - 1, де e₁ - число інтервалів, m - число параметрів, що розглядаються у вибірці.

Якщо виконується рівність x² <= x²_a, то вважається, що гіпотеза вірна.

7. В чому сутність критерію Пірсона (хі-квадрат) і з якою метою його використовують?

Критерій Пірсона - статистичний критерій для перевірки гіпотези, що спостережувана випадкова величина підпорядковується деякому теоретичного закону розподілу.

Ідея методу - визначення ступеня розбіжності відповідних частот f_екс і f _теор; чим більше ця розбіжність, тим більше значення x²

² =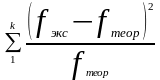 = ² =  {(l_i – N*p_i)² / N*p_i } i (1, I)

где:

I – количество интервалов;

l_i – фактическое количество элементов, попавших в i-тый интервал;

N*p_i – теоретическое количество элементов, которое должно попасть в i-тый интервал

² – величина рассогласования.

Критерій хі-квадрат використовується для перевірки гіпотези про збіг емпіричного і теоретичного розподілів дискретних випадкових величин. Критерій ґрунтується на порівнянні спостережених і очікуваних (теоретичних) значеннях.

Критерій хі-квадрат може застосовуватися при аналізі таблиць спряженості, що містять відомості про частоту випадків в залежності від наявності фактора ризику.