Филиал государственного бюджетного образовательного учреждения высшего профессионального образования Московской области «Международный университет природы, общества и человека «Дубна» - Дмитровский институт непрерывного образования (филиал ДИНО университета «Дубна»)

Кафедра математики и прикладной информатики

КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ

«ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ ВЫСОКОГО УРОВНЯ»

ТЕМА: «Разработка программы вычисления обратной матрицы»

Выполнила: студентка

0215-ЭК(о) группы

первого курса

направление: ПИ

Кондратьева Наталья Дмитриевна

Руководитель:

к.т.н., доцент Завьялов А.М.

Дата защиты:____________

Оценка: ________________

________________________

(подпись руководителя)

г. Дмитров, 2016

Оглавлени

Введение 4

Постановка задачи 5

Нахождение обратной матрицы методом Гаусса-Жордана. 6

БЛОК-СХЕМА 12

Интерфейс 15

Программный код 17

Вывод 20

Список используемой литературы 21

Оглавление 2

Введение 3

Постановка задачи 4

Метод Гаусса (метод последовательного исключения неизвестных) 5

БЛОК-СХЕМА 7

Интерфейс 8

Листинг программы 10

Вывод 17

Список используемой литературы 18

Введение

Данная курсовая работа является обобщающим итогом полученных знаний за 1-ый курс по “Программированию на языках высокого уровня” и “Линейной алгебре”. В данной работе мы рассмотрим алгоритм создания программы, которая сможет вычислять обратную матрицу. Также мы рассмотрим теоретическую часть, блок – схему и непосредственно сам листинг программы.

Постановка задачи

Цель: создание программы способной вычислять обратную матрицу

Исходные данные: Теория (решение обратной матрицы методом Гаусса - Жордана), среда разработки (Microsoft Visual Basic 6.0)

Представлении о модели:

• В программу можно вводить нужные нам данные

• Выдавать пользователю ответ

• Выдавать пользователю дополнительную информацию (Список разрешающих строк, исходную матрицу, конечную информацию)

• Иметь удобную навигационную систему

• Корректно выполнять решение

Ожидаемый результат: Корректно работающая программа

Критерии оценки результата: Главным критерием является в первую очередь правильность вычисления обратной матрицы. Также можно отнести к критериям удобство использования программы.

Нахождение обратной матрицы методом Гаусса-Жордана.

Суть нахождения обратной матрицы методом Гаусса-Жордана заключается в том, что если с единичной матрицей Е провести элементарные преобразования, которыми невырожденная квадратная матрица А приводится к Е, то получится обратная матрица A^-1 .

Теперь опишем алгоритм приведения матрицы А порядка n на n, определитель которой не равен нулю, к единичной матрице. Для начала преобразуем матрицу так, чтобы элемент a₁₁ стал равен единице, а все остальные элементы первого столбца стали нулевыми.

Если a₁₁=0, то на место первой строки ставится k-ая строка (k>1), в которой a_k1 ≠0, а на место k-ой строки ставится первая. (Строка с a_k1 ≠0 обязательно существует, в противном случае матрица A – вырожденная). После перестановки строк получили «новую» матрицу А, у которой a_k1 ≠0.

Теперь умножаем каждый элемент первой строки на  . Так приходим к «новой» матрице А, у которой a₁₁=1. Далее к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на -a₂₁ . К элементам третьей строки – соответствующие элементы первой строки, умноженные на –a₃₁. И продолжаем такой процесс до n-ой строки включительно. Так все элементы первого столбца матрицы А, начиная со второго, станут нулевыми.

Преобразуем матрицу А так, чтобы элемент a₂₂ стал равен единице, а все остальные элементы второго столбца, начиная с a₃₂ , стали нулевыми.

Если a₂₂=0, то на место второй строки ставится k-ая строка (k>2), в которой a_k2 ≠0, a на место k-ой строки ставится вторая. Так получаем преобразованную матрицу А, у которой a₂₂ ≠0. Умножаем все элементы второй строки на 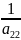 . После этого к элементам третьей строки прибавляем соответствующие элементы второй строки, умноженные на  –a₃₂. К элементам четвертой строки – соответствующие элементы второй строки, умноженные на –a₄₂. Следует продолжить такой процесс до n-ой строки включительно. Так все элементы второго столбца матрицы А, начиная с третьего, станут нулевыми, а a₂₂ будет равен единице.

Продолжаем процесс, пока все элементы главной диагонали матрицы А не станут равными единице, а все элементы ниже главной диагонали не станут равными нулю. С этого момента начинаем обратный ход метода Гаусса-Жордана. Теперь преобразуем матрицу А так, чтобы все элементы n-ого столбца, кроме a_nn, стали нулевыми. Для этого к элементам (n-1)-ой строки прибавляем соответствующие элементы n-ой строки, умноженные на –a_n-1n . К элементам (n-2)-ой строки – соответствующие элементы n-ой строки, умноженные на –a_n-2n . Такой процесс продолжаем до первой строки включительно. Так все элементы n-ого столбца матрицы А (кроме a_nn), станут нулевыми.

Преобразуем матрицу А так, чтобы все элементы (n-1)-ого столбца до a_n-1n-1 , стали нулевыми. Для этого к элементам (n-2)-ой строки прибавляем соответствующие элементы (n-1)-ой строки, умноженные на -a_n-2n-1 . К элементам (n-3)-ой строки – соответствующие элементы (n-1)-ой строки, умноженные на -a_n-3n-1 . И продолжаем такой процесс до первой строки включительно. Так все элементы (n-1)-ого столбца матрицы А (кроме a_n-1n-1 ), станут нулевыми. Действуя дальше схожим образом, мы получим единичную матрицу.

Пример №1:

Требуется найти для исходной матрицы А обратную матрицу А^-1 методом Гауcса.

Пример 1. Методом исключения Гаусса найдем матрицу, обратную к матрице

Решение:

К матрице A справа приписываем единичную матрицу того же порядка (А|E)

Приведем Матрицу (А|E) элементарными преобразованиями первого и второго типов к ступенчатому виду

→

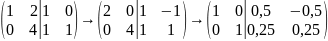
Последняя матрица имеет ступенчатый вид

3. Далее выписываем обратную матрицу. Это матрица, стоящая справа в последней преобразованной матрице.

В последней матрице слева стоит единичная матрица E.

Тогда матрица A^-1 будет иметь следующий вид:

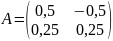
Пример №2.

Методом Гаусса найдем матрицу, обратную к матрице

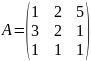
Решение:

К матрице А справа припишем единичная матрица того же порядка (А|E)

Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду

поменяем местами вторую и третью строки

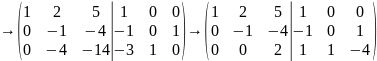
Последняя матрица имеет ступенчатый вид.

3. Полученная ступенчатая матрица элементарными преобразованиями 1-го, 2-го и 3-го типов приводим к виду, где слева будет матрица Е. Затем преобразования начинаются с последней строки.

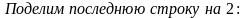
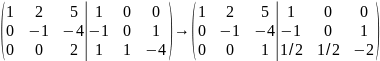
К элементам второй строки прибавляем элементы третьей, умноженные на 4, а к элементам первой строки - элементы третьей, умноженные на 5:

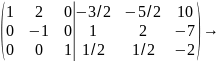
Все элементы второй строки умножим на (-1).

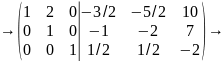
Из элементов первой строки вычитаем элементы второй, умноженные на 2.

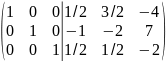
4. Выписывается обратная матрица. Это матрица, стоящая справа в последней преобразованной матрице.

В последней матрице слева стоит единичная матрица E.

Тогда матрица A^-1=