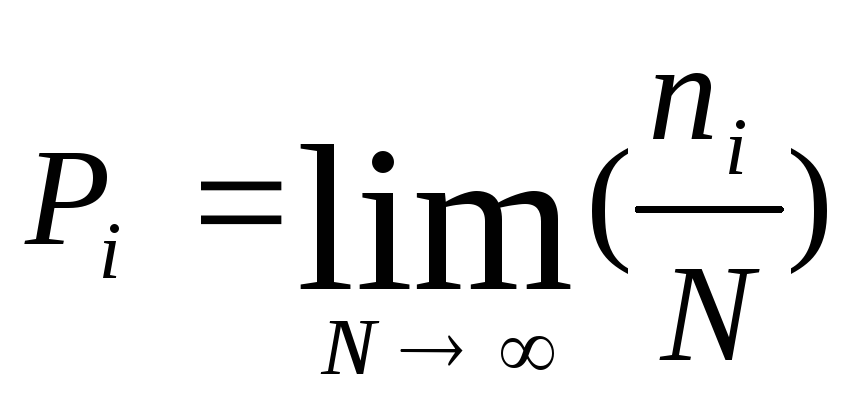Класичне визначення ймовiрностi

Ймовiрнiстю P(A) подiї A називається спiввiдношення m числа елементарних подiй, що сприяють подiї A, до числа N всіх елементарних подiй, Тобто

З наведеного класичного визначення ймовiрностi випливають наступнi її властивостi.

Iмовiрнiсть достовiрної подiї дорiвнює одиницi.

Дiйсно, достовiрнiй подiї повиннi сприяти всi N елементарних

подiй, тобто m = N i, отже,

Iмовiрнiсть неможливої подiї дорiвнює нулю.

Справдi, неможливiй подiї не може сприяти жодна з елементарних подiй, тобто m = 0, звiдки,

Ймовiрнiстю випадкової подiї є позитивне число мiж нулем та одиницею.

Дiйсно, випадковiй подiї сприяє лише частина iз загальногочисла елементарних подiй. Тому в цьому випадку 0 < m < N, значить, , Отже, 0 ≤ P(A) ≤ 1.

Тому, ймовiрнiсть будь-якої подiї задовольняє подвiйну нерiвнiсть.

З визначення ймовiрностi випливає, що елементарнi подiї є рiвноiмовiрними, тобто мають одну й ту саму iмовiрнiсть.

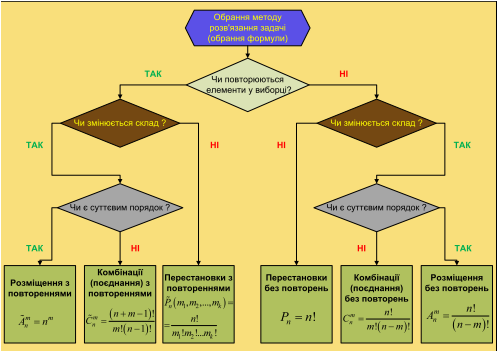
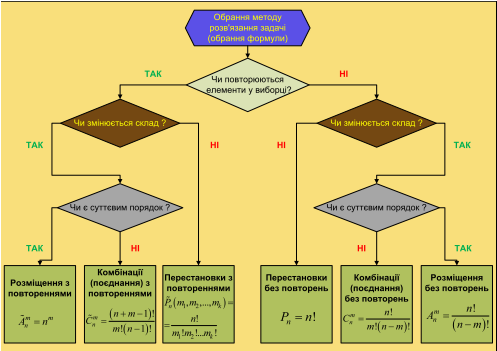
Застосування елементiв комбiнаторики до знаходження iмовiрностей

Комбiнаторика - роздiл математики, що вивчає питання про те, скiльки комбiнацiй певного типу можна скласти з даних предметів (елементiв). Як при вирiшеннi задач з використанням класичного визначення ймовiрностi, так i надалi нам знадобляться деякi формули комбiнаторики.

Наведемо найбiльш уживанi з них.

Комбінаторика

• Якщо з безлiчi предметiв обирається деяка пiдмножина, то її називають вибiркою.

• Вибiрки бувають впорядкованi i невпорядкованi.

• У впорядкованiй вибiрцi суттєвим є порядок, в якому слідують її елементи, iншими словами, змiнивши порядок елементiв, ми отримаємо iншу вибiрку.

Наприклад,

iз цифр 1, 2, 3, 4, 5 можна скласти наступнi тризначнi числа

123, 431, 524, ... i т.д.

Це впорядкованi трьохелементнi вибiрки, оскiльки 123 i 132 - рiзнi числа.

Або iнший приклад:

з 30-ти однакових деталей обрати двi - будь-яка пара деталей являє собою неупорядковану двохелементу вибiрку, оскiльки їх порядок не важливий.

Розміщення

Розмiщеннями з n рiзних елементiв по m елементiв (m ≤ n) називаються комбiнацiї, складенi з даних n елементiв по m елементiв, якi вiдрiзняються або самими елементами, або порядком елементiв.

Число розмiщень без повторень з n по m (n рiзних елементiв) обчислюється за формулою:

Розмiщеннями з повтореннями iз n елементiв по m називаються впорядкованi m-елементнi вибiрки, в яких елементи можуть повторюватися.

Число розмiщень з повтореннями обчислюється за формулою:

Наприклад, розглянемо, як iз трьох елементiв a,b,c можна скласти розмiщення по два елементи :

без повторень

ab, ac, bc, ba, ca, cb

(за формулою ()

з повтореннями

aa, bb, cc, ab, ac, bc, ba, ca, cb

(за формулою ()

Перестановки

Перестановками з n рiзних елементiвназиваються розмiщення з цих n елементiв по n.

Перестановки можна вважати окремим випадком розміщень при m = n.

Отже, число всiх перестановок iз n елементiв без повторень обчислюється за формулою: P_n = n(n − 1)(n − 2)... · 2 · 1 = n!

Число перестановок з повтореннями (k рiзних елементiв, де елементи можуть повторюватися m1, m2, ..., mk раз i

m₁ + m₂ + ... + m_k = n, де n - загальна кiлькiсть елементiв)

обчислюється за формулою:

Розглянемо попереднiй приклад, коли є три елементи a,b,c. Якi перестановки з цих букв можна отримати i скiльки таких наборiв вийде, якщо:

• лiтери в наборi не повторюються;

• лiтера a повторюється два рази?

Розв’язок

У першому випадку вийдуть набори: abc, acb, bac,bca, cab, cba.

За формулою (Pn = n!) маємо P₃ = 3! = 6.

У другому випадку вийдуть набори:

aabc, aacb, baca,bcaa, caab, cbaa, abac, acab, abca, acba, baac, caab.

За формулою () маємо

Поєднання

Поєднаннями (сполученнями) з n елементiв по m елементiв називаються комбiнацiї, складенi з даних n елементiв по m елементiв, якi рiзняться хоча б одним елементом.

Вiдмiннiсть сполучень вiд розмiщень в тому, що в сполученнях не враховується порядок елементiв.

Число поєднань (сполучень) без повторень (n рiзних елементiв,

узятих по m) обчислюється за формулою:

Числа є коефiцiєнтами у формулi бiнома Ньютона i тому часто називаються біноміальними коефiцiєнтами, якi можна знайти за допомогою трикутника Паскаля.

Число сполучень c повтореннями (n елементiв, узятих по m, де елементи в наборi можуть повторюватися) обчислюється за формулою

Схема визначення формули

Тема: «Основні характеристики теорії ймовірностей та випадкових величин».

Основні характеристики імовірності

Для наглядного подання основних характеристик імовірності розглянемо дослід з розподіленням частинок.

Позначимо і – це ящик, в котрий потрапляють частинки, hi – це висота рівня частинок,N – повна кількість частинок, H – це деякий масштабний коефіцієнт. Висота рівня частинок буде визначатися за формулою , де - це кількість частинок в і-тому ящику. Тоді імовірність потрапляння частинки до і-того ящика визначається за формулою: ,

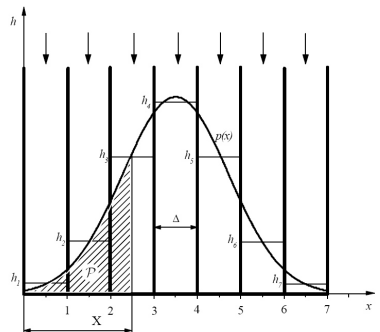
Якщо змоделювати ширину ящика, то дискретний розподіл ймовірностей переходить у неперервний, який визначається так званою густиною ймовірностей.

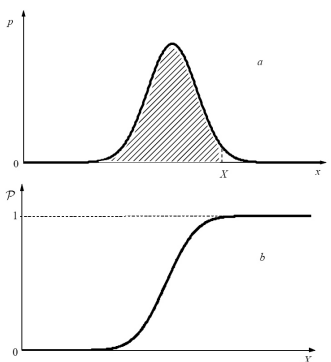
Слід мати на увазі, що частина ймовірності р(х) є локальною характеристикою, яка зама по собі змісту не має.

Якщо домножити густину імовірності на диференціал (чого небудь) то ми отримаємо велечину, що означає імовірнісне потрапляння частинки в інтервал .

Інтеграл цього співвідношення () дає повну кумулятивну імовірність.

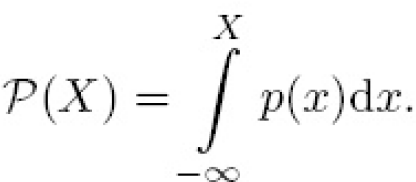
На границі визначення кумулятивної або повної імовірності приводить до умови нормування.

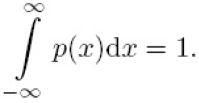
Якщо за допомогою густини розподілу можна знайти повну імовірність, то можна вирішити й зворотні задачі:

Густина ймовірності (р(х)) та кумулятивну імовірність (Р(х)) характеризує розподіл випадкових величин і зазвичай має вигляд:
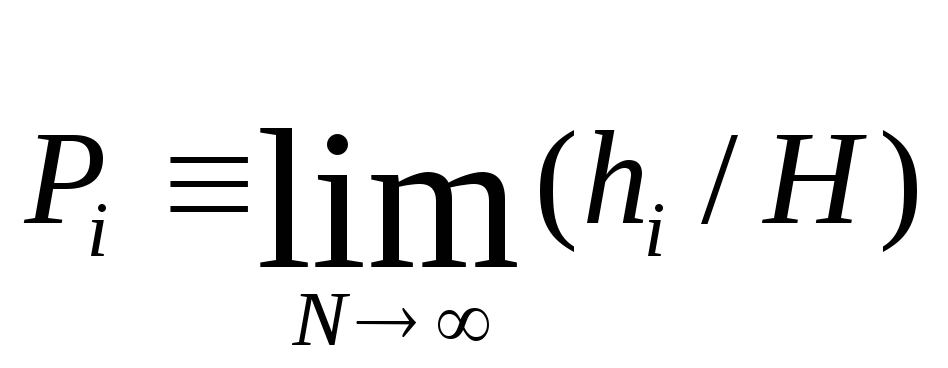