
7
.pdf
Гiстограма та полiгон частот
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
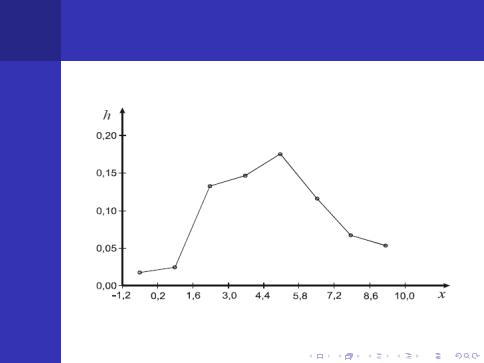
Полiгоном вiдносних частот називається ламана, що з’єднує точки середини iнтервалiв.
При збiльшеннi обсягу вибiрки i зменшеннi довжин iнтервалiв гiстограма i полiгон вiдносних частот
наближаються до графiком невiдомо¨ı функцi¨ı f (x) – густини
iмовiрностi сукупностi.
По виду гiстограми та полiгону частот можна висунути гiпотезу про вигляд розподiлу генерально¨ı сукупностi.
Гiстограма та полiгон частот
Iмовiрнiснi
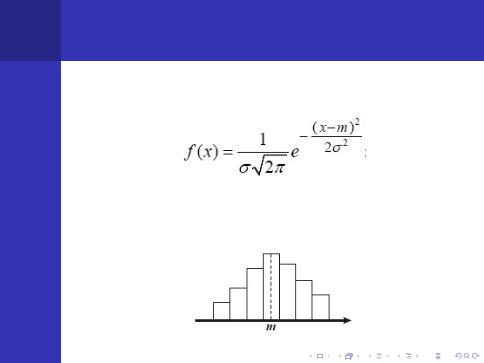
основи Нормальнiй розподiл (розподiл Гаусса)
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
Гiстограма та полiгон частот
Iмовiрнiснi
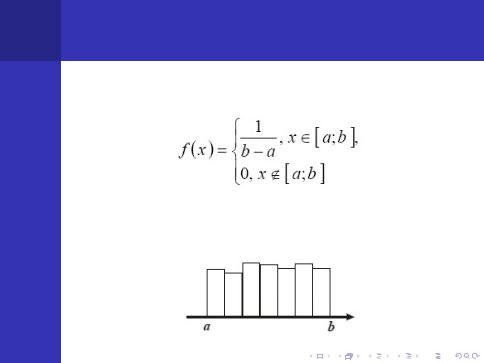
основи Рiвномiрний розподiл
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
Гiстограма та полiгон частот
Iмовiрнiснi
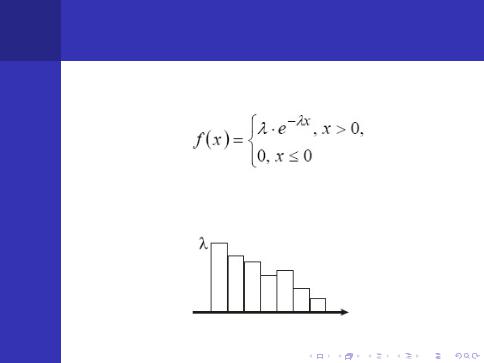
основи Експоненцiйний розподiл
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
Гiстограма та полiгон частот
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
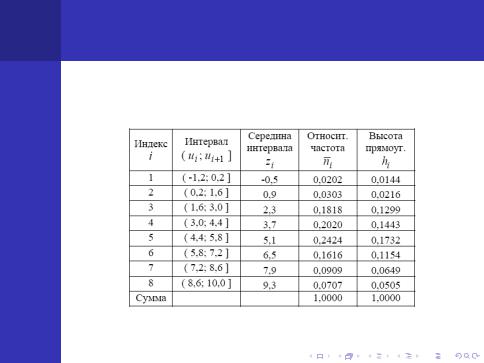
Для зручностi побудови полiгону вiдносних частот в третiй стовбчик додають середину iнтервалу
Гiстограма та полiгон частот
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
Гiстограма та полiгон частот
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q

Гiстограма та полiгон частот
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
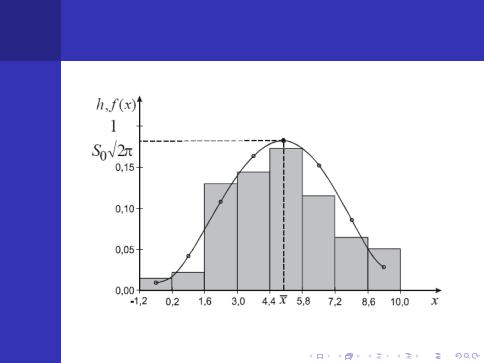
Гiстограма i полiгон вiдносних частот, є статистичними оцiнками густини iмовiрностей генерально¨ı сукупностi, схожi з кривою густини iмовiрностей нормального закону.
На пiдставi цього висувається нульовою гiпотезою. Генеральна сукупнiсть, з яко¨ı взята вибiрка, розподiлена за нормальним законом з параметрами
x = 4,9961 = 2,2657
тобто теоретична густина iмовiрностi має вигляд

Квантилi
Iмовiрнiснi
основи
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
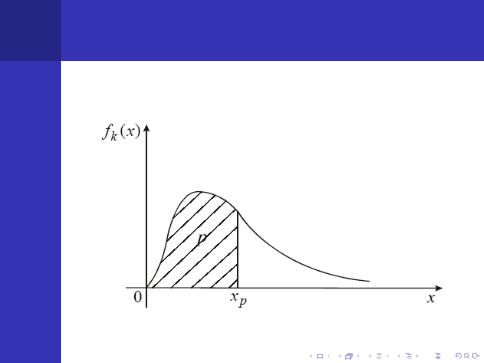
Квантиль, вiдповiдно¨ı ймовiрностi p, називається таке значення x, при якому виконується спiввiдношення:
Квантилi
Iмовiрнiснi
основи Геометричне пояснення квантилi
обробки
даних
Ющенко Ольга Володимирiвна
Статистичнi
ряди
Гiстограма та полiгон частот
Квантилi
Ящик з вусами
Графiк
Q − Q
