
1.4 Припущення про помилку.
Часто програміст з великим досвідом вишукує помилки "без жодних методів". При цьому він підсвідомо використовує метод "припущення про помилку". Процедура методу припущення про помилку в значній мірі заснована на інтуїції. Основна ідея методу полягає в тому, щоб перерахувати в деякому списку можливі помилки або ситуації, в яких вони можуть з'явитися, а потім на основі цього списку скласти тести. Іншими словами, вимагається перерахувати ті спеціальні випадки, які можуть не бути враховані при проектуванні.
2 Приклад вживання методів тестування «чорним ящиком»
Нехай необхідно виконати тестування програми, що визначає точку перетину двох прямих на площині. Попутно, вона повинна визначати паралельність прямої однієї їх осей координат.
В основі програми лежить рішення системи лінійних рівнянь:
Ax + By = C і Dx + Ey = F.
2.1. Використовуючи метод еквівалентного розбиття, одержуємо для всіх коефіцієнтів один правильний клас еквівалентності (коефіцієнт - дійсне число) і один неправильний (коефіцієнт - не дійсне число). Звідки можна запропонувати 7 тестів:
1) всі коефіцієнти - дійсні числа;
2)- 7) по черзі кожний з коефіцієнтів - не дійсне число.
2.2. По методу граничних умов:
-
можна вважати, що для початкових даних граничні умови відсутні (коефіцієнти - "будь-які" дійсні числа);
-
для результатів - одержуємо, що можливі варіанти: єдине рішення, прямі зливаються (безліч рішень), прямі паралелі (відсутність рішень). Отже, можна запропонувати тести, з результатами усередині області:
-
результат - єдине рішення ( 0);
-
результат - безліч рішень ( = 0 і x=y=0);
-
результат - відсутність рішень ( = 0, але x0 або у0);
-
і з результатами на границі:
-
= 0,01;
-
= -0,01;
-
= 0 x = 0,01 у = 0;
-
= 0 у = -0,01 x = 0.
-
2.3. По методу аналізу причинно-наслідкових зв'язків:
Визначаємо безліч умов.
а) для визначення типу прямої:
![]() - для визначення типа і існування першої
прямої;
- для визначення типа і існування першої
прямої;
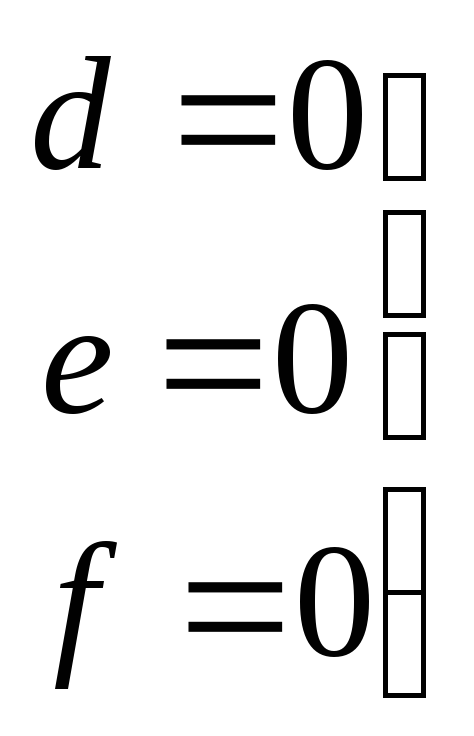 - для визначення типа і існування другої
прямої;
- для визначення типа і існування другої
прямої;
б) для визначення точки перетину:
= 0
x = 0
у = 0
Виділяємо три групи причинно-наслідкових зв'язків (визначення типу і існування першої лінії, визначення типу і існування другої лінії, визначення точки перетину) і будуємо таблиці істинності.
|
A=0 |
B=0 |
C=0 |
Результат |
|
0 |
0 |
X |
пряма загального положення |
|
0 |
1 |
0 |
пряма, паралельна осі ОХ |
|
0 |
1 |
1 |
вісь ОХ |
|
1 |
0 |
0 |
пряма, паралельна осі ОУ |
|
1 |
0 |
1 |
вісь ОУ |
|
1 |
1 |
Х |
безліч точок площини |
Така ж таблиця будується для другої прямої.
|
= 0 |
x = 0 |
у = 0 |
Єд. ріш. |
Кк.ріш. |
Ріш. нема |
|
0 |
X |
X |
1 |
0 |
0 |
|
1 |
0 |
X |
0 |
0 |
1 |
|
1 |
X |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
Кожний рядок цих таблиць перетвориться в тест. При нагоді (з урахуванням незалежності груп) беруться дані, відповідні рядкам відразу двох або всіх трьох таблиць.
В результаті до вже наявних тестів додаються:
-
перевірки всіх випадків розташування обох прямих - 6 тестів по першій прямій вкладаються в 6 тестів по другій прямій так, щоб варіанти не співпадали, - 6 тестів;
-
виконується окрема перевірка неспівпадання умови x = 0 або у = 0 (залежно від того, який тест був вибраний по методу граничних умов) - тест також можна сумістити з попередніми 6 тестами;
2.4. По методу припущення про помилку додамо тест:
-
всі коефіцієнти - нулі.
Всього одержали 20 тестів по всіх чотирьох методиках. Якщо ще спробувати вкласти незалежні перевірки, то можливо число тестів можна ще скоротити. (Не забудьте для кожного тесту наперед указувати результат!).
