Содержание

СОДЕРЖАНИЕ 3

1. ПОСТАНОВКА ЗАДАЧИ 4

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РЕШЕНИЯ ЗАДАЧИ 5

3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ 3

4. СХЕМА АЛГОРИТМА 4

5. ТАБЛИЦА ИДЕНТИФИКАТОРОВ 5

6. ТЕКСТ ПРОГРАММЫ 6

7. РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ 7

8. ГРАФИЧЕСКАЯ ЧАСТЬ 9

10

9. АНАЛИЗ РЕЗУЛЬТАТОВ 11

ЛИТЕРАТУРА 12

ПРИЛОЖЕНИЕ 13

Решение задачи с использование Microsoft Excel 13

1. Постановка задачи

Упругая призматическая балка (рис. 1) наглухо заделана в конце О и подвергается действию сосредоточенной вертикальной силы Р, приложенной к кон­цу балки L на расстоянии от места закрепления. Поперечное сечение балки - квадрат со стороной а. Весом балки пренебречь.

Исследовать прогибы балки y(x) при различных значениях силы P (весом балки пренебречь). Построить графики зависимостей y(x) в одних осях координат.

Исходные данные:

Длина стержня L=5м

Модуль упругости для стали

Сила

Сторона квадрата

Количество разбиений n=20

2. Математическая модель решения задачи

В качестве математической модели задачи используется дифференциальное уравнение изогнутой оси балки

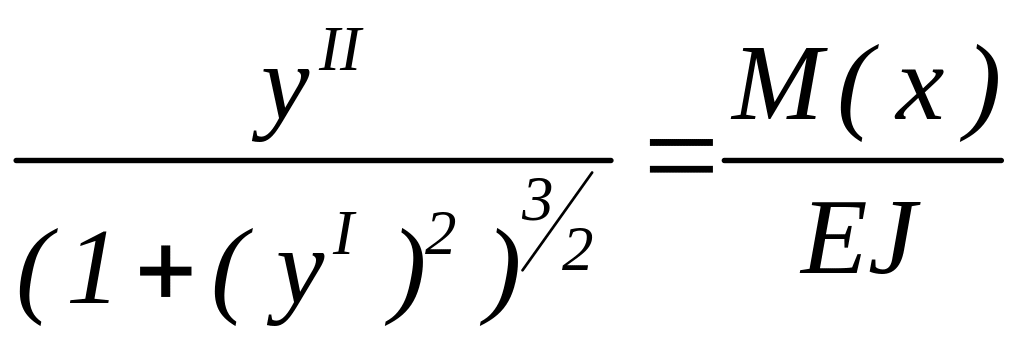
где М(x) – момент сил, приложенных к балке;

Е – модуль упругости;

J – момент инерции площади поперечного сечения балки;

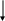
Р

В данном случае

,

начальные условия:

.

Задача Коши будет иметь вид

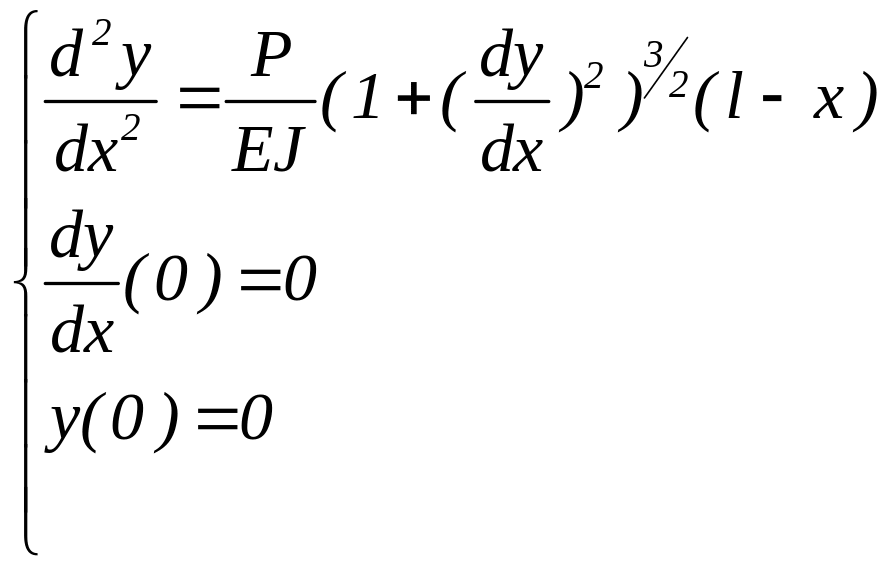
Преобразуем ее к системе дифференциальных уравнений 1-го порядка с начальными условиями

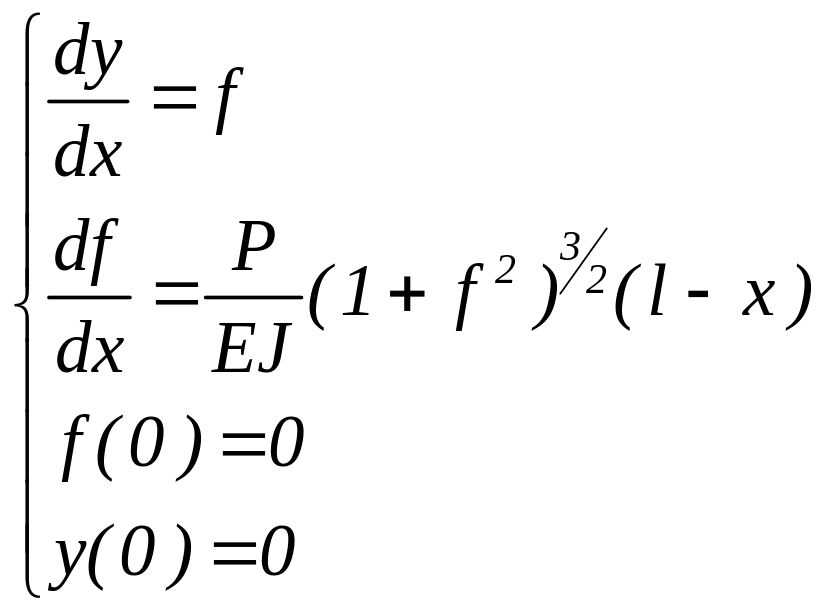
Решение дифференциальных уравнений методом Эйлера.

Пусть задано дифференциальное уравнение первого порядка или =F(x, y)

На интервале [x₀, x_n] разобьём на n частей и получим x_0,…,x_n.

x_i=x₀+ или x_i=x_i-1+h₁, где .

Соответствующее значения y₁=y*(x_i), где y*(x_i)- приближенное значение дифференциального уравнения.

Для получения численного решения дифференциального уравнения уравнение заменяется уравнениями относительно значений функции y*(x). Эти уравнения называют разностными. Простейшие разностные уравнения для заданного дифференциального уравнения имеют вид

y_i+1=y_i+ -формула Эйлера.

Алгоритм метода Эйлера.

1)Ввод исходных данных(x₀, x_n, n, y₀).

2) ; 3) Для i=1, n

4.1.)x_i=x_i-1+h;

4.2)y_i=y_i-1+ ;

4) Для i=0, n

5.1)Вывод x_i , y_i.

3. Алгоритм решения задачи

Вводим исходные данные

1. a, l, E, n;

2.Для k=1, 4

Ввод (P_k);

Выводим исходные данные

3. Вывод (a, l, P₁, P₂, P₃, P₄, E, n);

4. ;

Решаем дифференциальное уравнение методом Эйлера

5. Для k=1, 4

5.1. Вывод (x₁, y₁);

5.2. Для i=2, n+1

5.2.1.

5.2.2.

5.2.3.

5.2.4. Вывод (x_i, y_i);

Алгоритм функции fun

1.