
Теорія чисел в криптографії
.pdfМІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ І СПОРТУ СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
Кафедра прикладної та обчислювальної математики
ЗАСТОСУВАННЯ ТЕОРІЇ ЧИСЕЛ У КРИПТОГРАФІЇ
КОНСПЕКТ ЛЕКЦІЙ
Для студентів спеціальностей «Інформатика» та «Прикладна математика» денної та заочної форм навчання.
Суми Видавництво СумДУ
2010
Зміст |
|
стор. |
|
ТЕМА №1 ПОДІЛЬНІСТЬ ЦІЛИХ ЧИСЕЛ......................................................................................... |
3 |
Питання 1 Основні поняття та теореми. ............................................................................................... |
3 |
Питання 2 Найбільший спільний дільник (НСД). ............................................................................... |
5 |
Питання 3 Найменше спільне кратне (НСК)........................................................................................ |
8 |
Питання 4 Прості числа. Єдиність розкладання довільного цілого числа на прості множники. ... |
9 |
Питання 5. Ознаки подільності чисел................................................................................................. |
11 |
Питання 6 Неперервні дроби. .............................................................................................................. |
14 |
ТЕМА №2 НАЙВАЖЛИВІШІ ФУНКЦІЇ В ТЕОРІЇ ЧИСЕЛ. .......................................................... |
19 |
Питання 1. Функції виділення цілої та дробової частини дійсного числа. ..................................... |
19 |
Питання 2. Мультиплікативні функції................................................................................................ |
20 |
ТЕМА №3 ПОРІВНЯННЯ (КОНГРУЕНЦІЇ). ВЛАСТИВОСТІ ПОРІВНЯНЬ............................... |
26 |
Питання 1. Основні поняття та теореми. Властивості конгруенцій. ............................................... |
26 |
Питання 2. Повна та зведена системи лишків.................................................................................... |
28 |
Питання 3. Повні та зведені системи лишків, як структури теорії груп. Мала теорема Ферма та |
|
теорема Ейлера. ..................................................................................................................................... |
30 |
ТЕМА №4 КОНГРУЕНЦІЇ З ОДНИМ НЕВІДОМИМ...................................................................... |
36 |
Питання 1. Основні відомості.............................................................................................................. |
36 |
Питання 2. Конгруенції першого степеня. Розв’язання конгруенцій. ............................................. |
38 |
Питання 3 Обернений елемент за множенням. Повернення до питання про системи лишків, як |
|
структури теорії груп............................................................................................................................ |
40 |
Питання 4. Системи конгруенцій першого степеня з одним невідомим......................................... |
41 |
Питання 5 Конгруенції n-го степеня за простим модулем. Кількість коренів конгруенції n -го |
|
степеня за простим модулем................................................................................................................ |
44 |
Питання 6 Конгруенції n-го степеня за складеним модулем............................................................ |
47 |
ТЕМА №5 КОНГРУЕНЦІЇ 2-ГО СТЕПЕНЯ ..................................................................................... |
52 |
Питання 1 Загальні положення............................................................................................................ |
52 |
Питання 2 Квадратична конгруенція за простим непарним модулем p ........................................ |
53 |
Питання 3 Символ Лежандра............................................................................................................... |
55 |
Питання 4. Символ Якобі. .................................................................................................................... |
58 |
Список літератури................................................................................................................................. |
61 |
2

ТЕМА №1 ПОДІЛЬНІСТЬ ЦІЛИХ ЧИСЕЛ
Питання 1 Основні поняття та теореми. Питання 2 Найбільший спільний дільник (НСД). Питання 3 Найменше спільне кратне (НСК).
Питання 4 Прості числа. Єдиність розкладання довільного цілого числа на прості множники.
Питання 5 Ознаки подільності чисел. Питання 6 Неперервні дроби.
Ключові терміни
Цілі числа, дільник, кратне, власний дільник, нетривіальний дільник, просте число, складене число, неповна частка, залишок, спільний дільник, найбільший спільний дільник, взаємно прості числа, попарно прості числа, спільне кратне, найменше спільне кратне, алгоритм Евкліда, решето Ератосфена, канонічне розкладання, кількість дільників, неперервний дріб, підходящі дроби.
Питання 1 Основні поняття та теореми.
Теорія чисел розглядає цілі числа, тобто числа класу Z = 0,±1,±2... . та властивості цих
чисел. Сума та добуток цілих чисел є цілі числа, але про результат ділення двох цілих чисел такого стверджувати вже не можна.
Означення. Для довільних цілих чисел a і b визначається, що b ділить a , якщо існує таке ціле число q , для якого виконується рівність:
a = b × q
Позначається цей факт так: b | a . При цьому b - дільник числаa , відповідно число a за
таких умов кратне числу b .
Інший запис подільності числа a на число b – aMb . Читається цей запис так: число a ділиться на число b без залишку і відповідає рівності
a = q Z b
Власний дільник числа a - будь-який додатний дільник a , відмінний від a .
Нетривіальний дільник a - будь-який додатний дільник a , який не дорівнює 1 та a .
Просте число є таке ціле число, яке має за дільники тільки 1 та a . Ціле число, яке має хоча б один нетривіальний дільник, називається складеним числом.
Властивості подільності цілих чисел.
1.Якщо b | a і c - будь-яке додатне ціле число, тоb | a × c .
2.Якщо b | a та c | b , то c | a .
3.Якщо b | a та b | c , то b | a + c .
4.Узагальнення: якщо у рівності k + l + ... + n = p + q + ... + s про всі числа, крім
одного відомо, що вони кратні числу b , то і це останнє є кратним b .
Теорема про ділення з залишком. Будь-яке ціле число a єдиним способом подається за допомогою додатного цілого числа b рівністю:
a = b × q + r, 0 £ r < b ,
де q - неповна частка, r - залишок
Очевидно, що за умови r = 0 q є повна частка, а b | a .
3

Якщо просте число p є неоднократним дільником довільного цілого числа a (число a ділиться на p α -разів, α - ціле невід’ ємне число), то цей факт будемо позначати так: p α | a . В цьому випадку p α | a , а p α+1
Приклади.
1. Відомо, що неповна частка q ділення числа a = 56839 на деяке невідоме ціле число b дорівнює 224. Знайти число b і залишок від ділення r .
Розв’язання.
Число a = 56839 єдиним способом можна подати так: a = b × q + r . Підставимо у цей вираз відомі числа.
56839 = b × 224 + r |
56839 |
= b + |
r |
|
= 25 + |
83 |
, |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
224 |
|
|
224 |
|
|
|
|
|
224 |
|
|
|
|
|
|
|
|
||||||||
Відповідь. b = 25, |
r = 83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
Довести, |
що |
поліном |
xn + a |
|
xn −1 |
+ a |
|
|
xn −2 + ... + a x + a = 0, |
a Î Z , i = |
|
якщо має |
||||||||||||||||||||
|
n −2 |
0, n |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n −1 |
|
|
|
|
|
|
|
|
1 |
0 |
i |
||||||
раціональні корені, то тільки цілі α Î Z . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Нехай |
поліном |
має раціональний |
|
корінь |
α = |
k |
- |
нескорочуваний дріб, k,l Î Z . |
|||||||||||||||||||||||||
|
l |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Підставимо корінь до поліному: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
k n |
k n −1 |
|
|
|
k |
n − 2 |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
+ a |
|
|
|
+ a |
n −2 |
|
|
|
|
+ ... + a |
|
|
|
+ a |
|
= 0 , |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
l |
n −1 l |
|
|
l |
|
|
|
1 l |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
Умножимо обидві частини поліному на l n . Отримаємо еквівалентний поліном |
|||||||||||||||||||||||||||||||||
k n + an −1 × l × k n −1 + an− 2 × l 2 × k n − 2 + ... + a1 × l n −1k + a0l n |
= 0 |
|
|
|
|
|
|
||||||||||||||||||||||||||
В останній рівності про всі доданки, крім першого відомо, що вони діляться на l . За властивістю 4 подільності чисел маємо, що k n Ml теж, тобто l | k , хоча за припущенням
α= k - нескорочуваний дріб. Прийшли до протиріччя. l
Висновок:
Отже, якщо даний поліном має раціональний корінь, то він цілий.
3. Показати, що якщо п’ятизначне ціле число ділиться на 41, то всі числа, отримані перестановкою цифр цього числа по колу теж діляться на 41.
Розв’язання
Будь-яке п’ятизначне число подається в десятковій системі числення так
N = 105 a +104 a |
4 |
+103 a +102 a |
2 |
+10a + a , |
"a Î Z : 0 £ a £ 9, i = 0,1,2,3,4,5 |
|
5 |
3 |
1 0 |
i |
i |
||
Переставимо по колу старшу цифру на останнє місце
N |
1 |
=105 a |
4 |
+10 |
4 a |
3 |
+103 a |
2 |
+102 a +10a |
0 |
+ a |
5 |
=10(104 a |
4 |
+103 a |
3 |
+10 |
2 a |
2 |
+10a + a |
0 |
)+ a |
5 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
В дужках число можна добудувати до вихідного числа N , додавши і віднявши 105 a5 |
|
||||||||||||||||||||||||||||||||||||||||
|
N |
1 |
= 10(105 a |
5 |
+ 104 a |
4 |
+ 103 a |
3 |
+10 |
2 a |
2 |
+10a + a |
0 |
-105 a |
5 |
)+ a = 10N -106 a |
5 |
+ a |
5 |
= 10N - 99999a |
5 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Оскільки вихідне число |
N |
ділиться на 41 за умовою, |
то для того, щоб отримане |
||||||||||||||||||||||||||||||||||||
число N1 |
ділилося на 41 необхідно щоб другий доданок правої частини 99999a5 ділився |
||||||||||||||||||||||||||||||||||||||||
на 41. Про a5 |
|
нічого не відомо, отже на 41 повинно ділитися число 99999. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Перевіримо: |
|
99999 |
= 2439 N1 M41 , що і потрібно було показати. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Висновок:
4

Якщо довільне п’ятизначне ціле число ділиться на 41, то всі числа, отримані перестановкою цифр цього числа по колу теж діляться на 41.
4. Показати, що "n Î N 2n |(n +1)×(n + 2)×...×(2n)
Розв’язання.
Звернемо увагу, що даний добуток складає другу половину 2n!. Якщо цей добуток умножити та поділити на n!, отримаємо
(2n)! = 1× 2 ×3×...× 2n
n! n!
Перегрупуємо чисельник, записавши спочатку усі непарні числа, а потім усі парні.
(2n)! = 1×3×5 ×...×(2n -1)× 2 × 4 ×6 ×...× 2n = 1×3×5 ×...×(2n -1)× 2n (1× 2 ×3×...× n) =
n! |
n! |
|
|
|
|
n! |
||
= |
1× 3 × 5 ×... × (2n -1)× 2n n! |
= 1× 3 × 5 ×... × (2n -1)× 2n M2n , що і потрібно було показати. |
||||||
|
|
|||||||
|
n! |
|
|
|
(n +1)×(n + 2)× ...×(2n) |
|
|
|
|
Висновок: "n Î N : |
|
Î Z |
|
||||
|
|
|
|
|
||||
|
|
|
|
|
2n |
|
||
5. Показати, що натуральне число m5 - m ділиться на 30. |
||||||||
Розв’язання. |
|
|
|
|
|
|
|
|
Використаємо |
для доведення комбінаторну |
формулу кількості сполучень з n |
||||||
елементів по k : |
Cnk = |
n(n -1)(n - 2)...(n - k +1) |
Î N . |
Ця формула являє собою факт, що |
||||
|
||||||||
|
|
|
|
|
k! |
|
||
добуток з послідовних k |
натуральних чисел націло ділиться на k! |
|||||||
Число 30 = 6 ×5 = 3!×5
Розглянемо надане у прикладі число і застосувавши до нього формули алгебраїчних перетворень, спробуємо виділити відповідні послідовності чисел:
m5 - m = m(m4 -1)= m(m2 -1)(m2 + 1)= (m -1)m(m + 1)(m2 - 4 + 5)= (m -1)m(m +1)(m2 - 4)+
+ 5(m -1)m(m + 1) = (m - 2)(m -1)m(m +1)(m + 2) + 5(m -1)m(m + 1)
Упершому доданку маємо добуток 5-ти послідовних чисел. Тобто перший доданок ділиться націло на 5! = 120 = 30 × 40 . Перший доданок на 30 ділиться.
Удругому доданку маємо добуток послідовних 3-х чисел та числа 5, тобто другий доданок ділиться на 3!×5 = 6 ×5 = 30
Висновок: Обидва доданки розкладання числа m5 - m діляться на 30, отже і само число ділиться на 30.
Питання 2 Найбільший спільний дільник (НСД).
Не звужуючи загальної теорії будемо у подальшому розглядати тільки додатні дільники чисел.
1. Будь-яке ціле di , яке одночасно ділить числа a, b,...., l носить назву спільний дільник
(СК) цих чисел. Найбільший із всіх дільників носить назву найбільший спільний дільник (НСД) та позначається d = (a, b,...., l )
2. Якщо (a, b,...., l ) = 1 , то числа a, b,...., l - взаємно прості, якщо кожне число з наведеного
набору є взаємно простим з кожним іншим числом цього набору, то ці числа – попарно прості. Попарно прості числа є одночасно і взаємно простими, але не навпаки.
5
Приклад: Числа 6, 10, 15 – взаємно прості, бо (6,10,15) = 1 , але вони не попарно прості. Числа 7, 13, 23 – попарно прості, бо (7,13) = (7,23) = (13,23) = 1 , і одночасно вони взаємно прості.
НСД двох цілих чисел а і b.
1. Якщо b | a , то (a, b) = b і кількість дільників у чисел a та b співпадає з кількістю
дільників b .
2. Якщо a = bq + r , то кількість дільників a співпадає із кількістю спільних дільників b та r , зокрема
(a, b) = (b, r ) ( витікає з властивості 4. п.1.1).
3. Якщо a0 = cq0 + r0 , a1 = cq1 + r1 ,..., an = cqn + rn (a0 , a1 ,..., an , c) = (c, r0 , r1 ,...rn )
Алгоритм Евкліда для знаходження НСД двох чисел a і b .
Цей алгоритм ґрунтується на попередніх твердженнях. Розглянемо a та b , причому a ³ b . Тоді можна записати обмежений ланцюжок ділень з залишком:
a = bq0 + r1; |
0 < r1 < b |
|
b = r1q1 + r2 ; |
0 < r2 |
< r1 |
r1 = r2 q2 + r3 ; 0 < r3 |
< r2 |
|
.................... |
|
|
rn−2 = rn−1qn−1 + rn ; |
0 < rn < rn−1 |
|
rn−1 = rn qn |
|
|
Останнє ділення – |
ділення без залишку, тобто rn | rn−1 . |
|
Досліджуючи цей ланцюжок з останнього ділення уверх, отримаємо: rn | rn−1 rn | rn−2 (rn−2 , rn−1 ) = rn ;
rn | rn−2 rn | rn−3 (rn−3 , rn−2 ) = (rn−2 , rn−1 ) = rn ;
.......................................
rn |
| r1 rn |
| b (b, r1 ) = ...... = rn ; |
rn |
| b rn |
| a (a, b) = ...... = rn |
Отже,
-сукупність дільників a та b співпадає з сукупністю дільників їх НСД.
-НСД a та b дорівнює останньому ненульовому залишку в ланцюжку ділень
за алгоритмом Евкліда. Узагальненням алгоритму Евкліду буде теорема:
Спільний дільник двох довільних цілих чисел d = (a,b) можна єдиним способом подати лінійною комбінацією цих чисел:
d = ax + by, x, y Î Z , x ¹ 0, y ¹ одночасно.
Доведення теореми витікає з алгоритму Евкліду, якщо всі залишки, починаючи з rn = d поступово виразити через попередні залишки, а потім і через a та b .
Приклад:
1. Знайти НСД a=648 та b=261. 2. Знайти x, y : d = ax + by .
Розв’язання:
1. Шукаємо НСД
6
|
648 |
: |
648 = 261× 2 +126; |
a = bq |
|
+ r , r = 126, 0 < 126 < 261 |
|||
|
|
|
0 |
||||||
261 |
|
|
1 |
1 |
|||||
|
|
|
|
|
|||||
|
261 |
: 261 = 126 × 2 + 9, |
b = r q |
+ r |
r = 9, 0 < 9 < 126 |
||||
|
|
||||||||
126 |
|
|
|
|
1 |
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||
|
126 |
: |
126 = 9 ×14 + 0, |
r = 0 |
|
|
|
||
|
|
|
|
||||||
9 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
r2 = 9 . Отже, (648,261) = 9 |
|||
Останній ненульовий залишок - |
|||||||||
2. Шукаємо подання НСД лінійною комбінацією:
d = r2 = b - r1q1 ; r1 = a - bq0 d = b - (a - bq0 )q1 = a(- q1 )+ b(1 + q0 q1 ) = -2a + (1+ 4)b = -2a + 5b
Отже x = −2, y = 5
Деякі властивості НСД:
1. |
Якщо (a, b) "m Î Z : (am, bm) = m(a, b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a b |
|
(a, b) |
|
|
a |
|
b |
|
|
(a, b) |
|
|
|||||||
2. |
Якщо d | a, d | b, "d Î Z |
|
, |
|
|
= |
|
|
, зокрема |
|
|
|
, |
|
|
= |
|
|
= 1 |
, тобто |
|
|
d |
|
|
|
(a, b) |
||||||||||||||
|
d |
|
d |
|
|
(a, b) |
|
(a, b) |
|
|
|
|||||||||
два будь-яких цілих числа, поділених на НСД цих чисел є взаємно простими числами.
3.Якщо (a, b) = 1 (ca, b) = (c, b);
4.Якщо (a, b) = 1. b | ac b | c ;
5.Якщо a1 , a2 ,..., am взаємно прості з кожним з b1 , b2 ,..., bn , то добуток a1 × a2 ×... × am взаємно простий з добутком b1 × b2 ×... × bn
7
Питання 3 Найменше спільне кратне (НСК).
Дані числа a1 , a2 ,..., am . Кожне з чисел, що є кратним кожному з даних чисел, носить
назву спільне кратне (СК). Найменше із усіх кратних називається найменше спільне кратне даних чисел.
Нехай (a, b) = d , тоді a = a1d , |
b = b1d і (a1 , b1 ) = 1 (властивості НСД, 2.) Нехай M - деяке |
|||||||||||||||
кратне a та b , тобто M = ka і |
|
M |
= |
ka |
= |
ka1d |
= |
ka1 |
Î Z . Оскільки (a , b ) = 1 , то k повинно |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
b b b1d |
1 |
1 |
||||||||
|
|
|
|
|
|
|
b1 |
|
||||||||
ділитися на b1 , тобто k = b1t . Для СК буде вірна формула: |
|
|||||||||||||||
M = ka = ak = ab t = |
ab1d |
t = |
a × b |
t |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
d |
|
|
|
d |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Найменше значення СК буде за умови, що t |
= 1, тобто для НСК виконується формула: |
|||||||||||||||
[a,b]= m = |
ab |
|
, тоді M = m × t |
|
|
|
|
|||||||||
(a,b) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теореми:
1.Сукупність спільних кратних чисел a та b співпадає з сукупністю кратних для їх НСК.
2.НСК a та b дорівнює відношенню добутку цих чисел до їх НСД.
8

Питання 4 Прості числа. Єдиність розкладання довільного цілого числа на прості множники.
1. Вислови:
1.Число 1 має тільки один додатний дільник – самого себе. Одиниця стоїть осторонь у ряду натуральних чисел.
2.Найменший дільник, що не дорівнює 1, для будь-якого цілого числа є число
просте. (Візьмемо число a і його найменший дільник q ¹ 1 . Допускаємо, що q = q1 × r, q1 £ q, r £ q . Тоді a ділиться на q1 і на r , тобто a має дільник, менший за q , що є протиріччям вихідному посиланню.)
3. Найменший дільник, що не дорівнює 1, для будь-якого складеного цілого числа a
не перевищує значення 
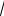 a . (Нехай a = q × c . Оскільки q - найменший дільник, то c ³ q .
a . (Нехай a = q × c . Оскільки q - найменший дільник, то c ³ q .
Отже ac ³ q 2 c, a ³ q 2 , або q £ 
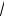 a .
a .
4.Простих чисел безкінечно багато.
5.Решето Ератосфена для вибору простих чисел, які не перевищують даного числа
N.
1)Обираємо перше просте число – p1 = 2 . Викреслюємо всі цілі числа з інтервалу (4, N ), кратні 2.
2)Обираємо наступне найменше просте число p2 = 3 . Викреслюємо всі цілі числа з інтервалу (9, N ), кратні 3.
3)Повторюємо процес з наступним p3 = 5 .
4)Обираючи чергове pk , звертаємо увагу на те, що кандидатів на викреслення
слід розглядати починаючи з числа pk 2 , бо всі менші складені числа викреслені, як такі, що кратні простим числам, меншим за pk .
5)Викреслення можна зупинити, коли pk перевищить 
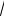 N . Усі складені числа на той час будуть викреслені.
N . Усі складені числа на той час будуть викреслені.
2.Єдиність розкладання довільного цілого числа на прості множники.
Базові вислови для складених чисел:
∙Довільне ціле a або взаємно просте з даним простим числом p < a , або ділиться на нього.
∙Якщо добуток декількох множників ділиться на просте число p , то хоча б один з множників теж ділиться на p .
∙Довільне ціле число можна розкласти на добуток простих множників єдиним способом. (враховуючи комутативність множення)
a= p1 × p2 ×... × pn
∙У наведеному розкладанні деякі з множників можуть повторюватися не
один раз. Позначивши через p1 , p2 ,..., pk тільки різні множники, а через a1 , a2 ,..., ak відповідні кратності входження множників до числа a ,
запишемо канонічне розкладання довільного цілого числа a на множники:
a = p1α1 × p2 α2 ×... × pk αk
9
∙
d = p1β1 × p2 β2
Нехай |
a = p α1 × p |
α2 ×... × p |
|
αk |
- канонічне розкладання довільного цілого |
||
|
1 |
|
2 |
|
k |
|
|
числа |
a . Тоді усі дільники цього числа можна подати у канонічному |
||||||
вигляді: |
|
|
|
|
|
|
|
×... × pk βk |
, де 0 £ bi |
£ ai , |
i = |
|
|
||
1, k |
|
||||||
∙У відповідності до вищенаведеної формули, кількість дільників τ довільного цілого числа a можна знайти так:
τ= (α1 +1)(α 2 +1)...(α k +1)
∙Розглянемо канонічне розкладання m довільних цілих чисел:
ai = pi1αi1 |
× pi 2 |
αi 2 |
×...× pik αik , |
i = |
|
|
|
|
|
|
|
|
|
|
||||||
1, m |
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тоді НСД цих чисел у канонічному вигляді має вигляд: |
|||||||||||||||||||
min (αi1 ) |
|
|
min (αi 2 ) |
|
|
min (αik |
) |
|
|
|
|
|
|
|
|
|||||
|
|
×... |
, i = 1, m |
|
|
|
|
|
||||||||||||
d = pi1i =1,m |
|
× pi 2 i =1,m |
|
× pik i =1,m |
|
|
, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а НСК – |
(αi1 ) |
|
|
(αi 2 ) |
|
|
max (αik |
) |
|
|
|
||||||||
|
|
|
|
max |
|
max |
|
|
|
|
|
|||||||||
|
m = |
|
|
|
, i = 1, m |
|||||||||||||||
|
pi1i=1,m |
|
|
× pi 2 i=1,m |
|
|
×... × pik i =1,m |
|
|
|||||||||||
∙Сукупність спільних дільників декількох цілих чисел співпадає з кількістю дільників НСД цих чисел.
∙НСК декількох взаємно простих чисел дорівнює їх добутку, а сукупність кратних декількох чисел співпадає з сукупністю кратних НСК цих чисел.
Приклад:
Дані 2 числа 12348 та 867. Побудувати канонічну форму цих чисел, знайти їх НСД та НСК.
Розв’язання:
а) 12348 за ознаками ділення ділиться на 4(22) і на 9 (32)
12348 = 3087 × 22 = 22 × 32 × 343 = 22 × 32 × 73 - канонічне розкладання числа. Дільників у цього числа буде τ = (2 +1)(2 +1)(3 +1) = 36
б) 867 = 3 ×172 - канонічне розкладання другого числа. Дільників у другого числа буде
τ = (1+1)(2 +1) = 6 : 1, 3, 17, 289, 51 та 867
НСД - d = (12348,867) = 2min (2,0)3min (2,1)7 min (3,0)17min (0,2) = 3
НСК - m = 2max (2,0)3max (2,1)7max (3,0)17max (0,2) = 223273172 = 4235364
10
