Практична робота № 12

Тема: Асиметричні криптосистеми. Криптосистема шифрування даних RSA

Мета: Навчитися зашифровувати і розшифровувати повідомлення алгоритмом RAS, встановлювати електроні підписи повідомлення.

Теоретичні відомості

1 Концепція криптосистеми з відкритим ключем

Ефективними системами криптографічного захисту даних є асиметричні криптосистеми, які називають також криптосистемами з відкритим ключем.

Рисунок 1 – Узагальнена схема асиметричної криптосистеми

Характерні риси асиметричних криптосистем:

1. Відкритий ключ 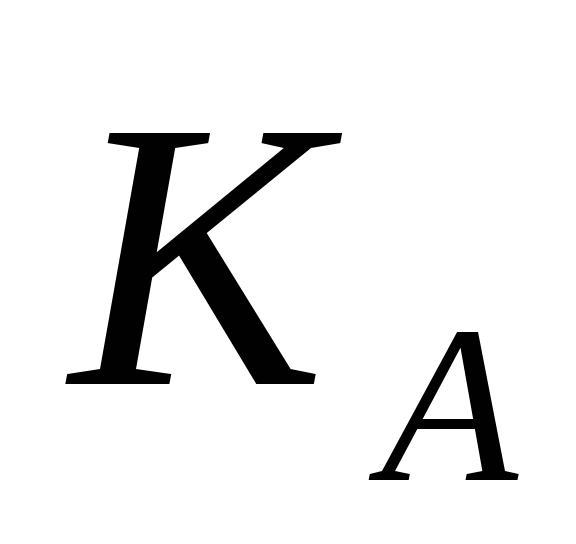і криптограма C можуть бути відправлені по незахищених каналах, тобто зловмиснику відомі значення 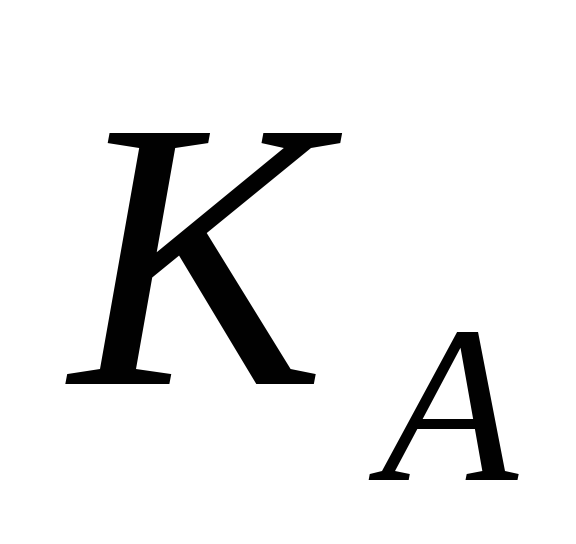та C.

2. Алгоритми шифрув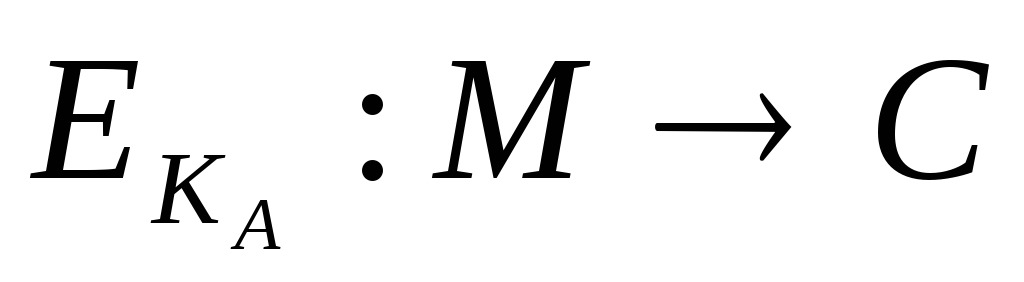ання () і розшифрування 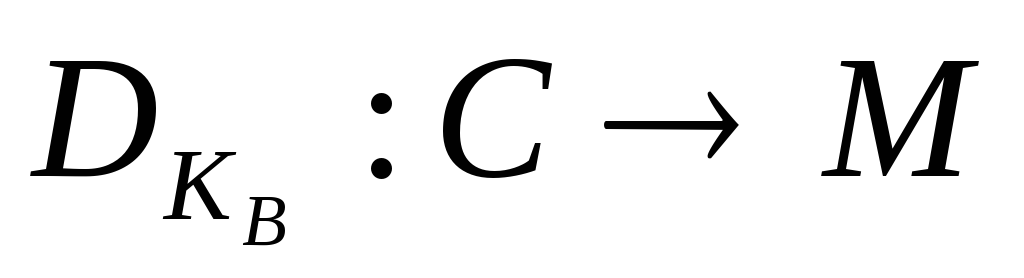є відкритими.

Захист інформації в асиметричній криптосистемі засновано на таємності ключа .

У.Діффі та М.Хеллман сформулювали вимоги, які забезпечують безпеку асиметричної криптосистеми:

1. Обчислення пари ключів (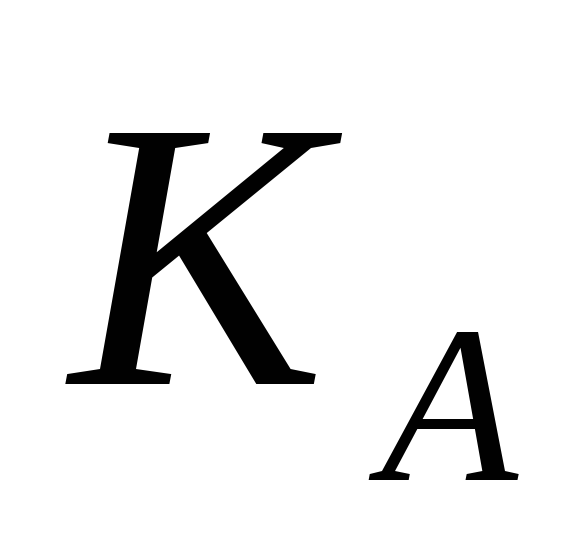, 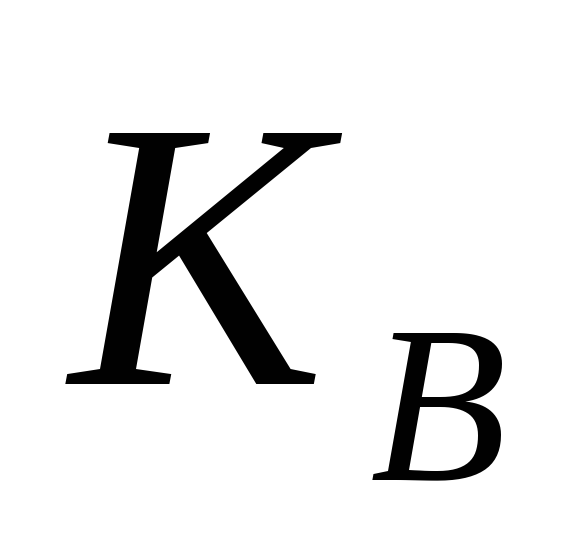) одержувачем B на основі початкової умови повинно бути простим.

2. Відправник A, знаючи відкритий ключ 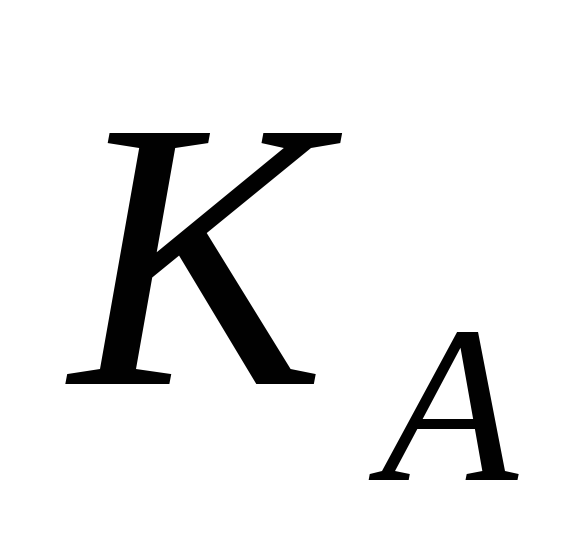і повідомлення М, може легко обчислити криптограму

. (4.1)

3 Одержувач В, використовуючи таємний ключ і криптограму C, може легко відновити вихідне повідомлення

. (4.2)

4 Зловмисник, знаючи відкритий ключ , при спробі обчислити таємний ключ натрапляє на непереборну обчислювальну проблему.

5 Зловмисник, знаючи пари (, C), при спробі обчислити вихідне повідомлення M натрапляє на непереборну обчислювальну проблему.

2 Односпрямовані функції

Концепція асиметричних криптографічних систем з відкритим ключем заснована на застосуванні односпрямованих функцій. Неформально односпрямовану функцію можна визначити в такий спосіб.

Нехай Х і Y – деякі довільні множини. Функція є односпрямованою, якщо для всіх можна легко обчислити функцію , але для більшості досить складно одержати значення , таке, що (при цьому вважають, що існує принаймні одне таке значення ).

Тому, задачу обернення функції називають задачею знаходження дискретного логарифма або задачею дискретного логарифмування.

Задача дискретного логарифмування формулюється в такий спосіб.

Для відомих цілих знайти ціле число , таке, що

.

Другим важливим класом функцій, що використовуються при побудові криптосистем з відкритим ключем, є односпрямовані функції з "потаємним ходом".

Функція належить до класу односпрямованих функцій з "потаємним ходом" у тому випадку, якщо вона є односпрямованою й, крім того, можливо ефективне обчислення зворотної функції, якщо відомо "потаємний хід" (таємне число, рядок або інша інформація, що асоціюється з даною функцією).

3 Криптосистема шифрування даних RSA

Алгоритм RSA запропонували в 1978 р. Р.Райвест (Rivest), А.Шамір (Shamir) і А.Адлеман (Adleman)

Надійність алгоритму ґрунтується на труднощі факторизації великих чисел і труднощі обчислення дискретних логарифмів.

Процедури шифрування та розшифрування в криптосистемі RSA

Припустимо, що користувач A хоче передати користувачеві B повідомлення в зашифрованому вигляді, використовуючи криптосистему RSA. У такому випадку користувач A є в ролі відправника повідомлення, а користувач B – у ролі одержувача. Як відзначалося вище, криптосистему RSA повинен сформувати одержувач повідомлення, тобто користувач В. Розглянемо послідовність дій користувача В і користувача A.

1. Користувач B вибирає два довільних великих простих числа P й Q.

2. Користувач B обчислює значення модуля N згідно з  

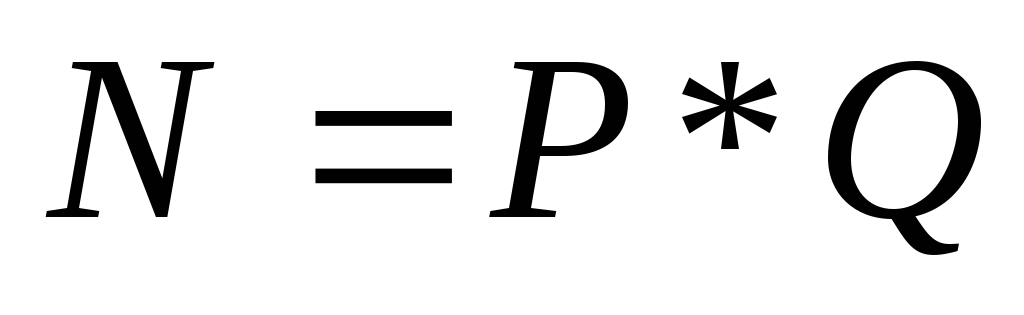
3. Користувач B обчислює функцію Ейлера 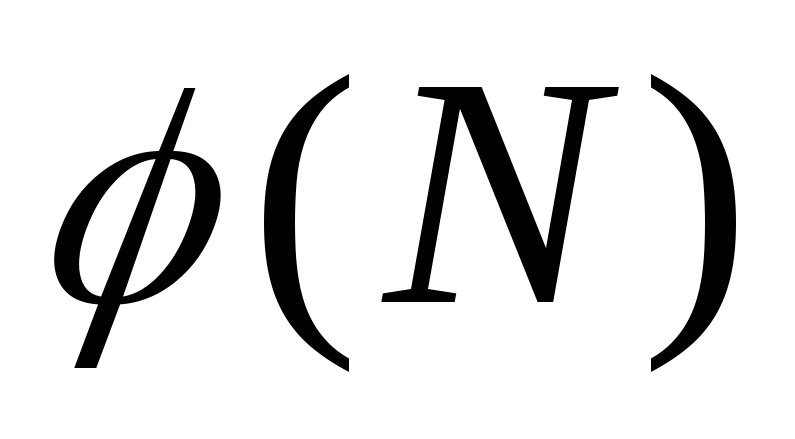й вибирає значення відкритого ключа 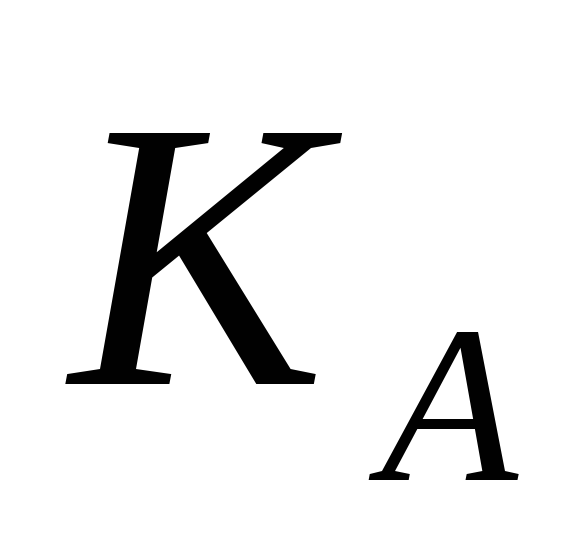з урахуванням виконання умов ,

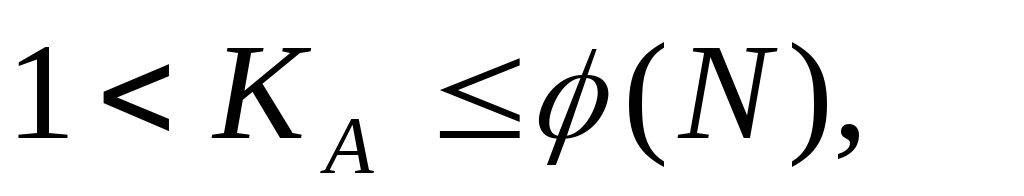
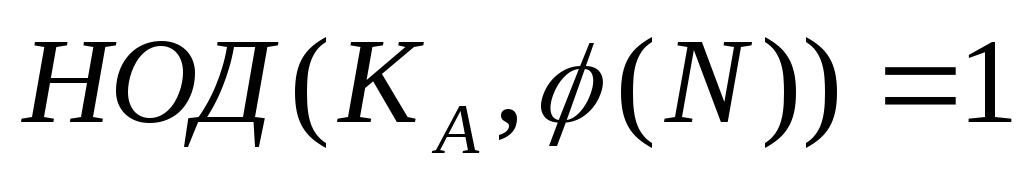4. Користувач B обчислює значення таємного ключа 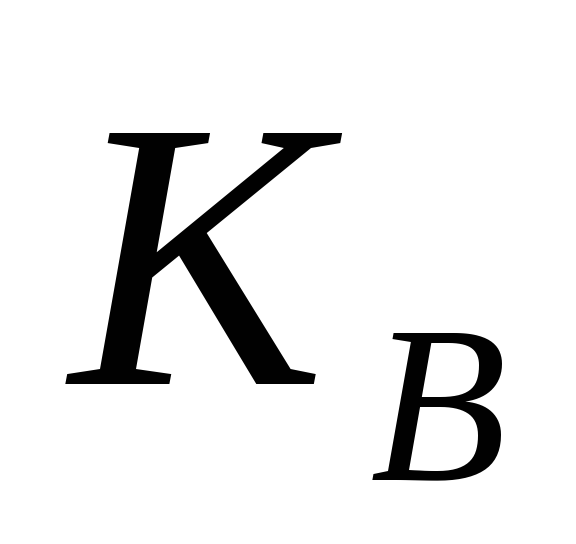за формулою 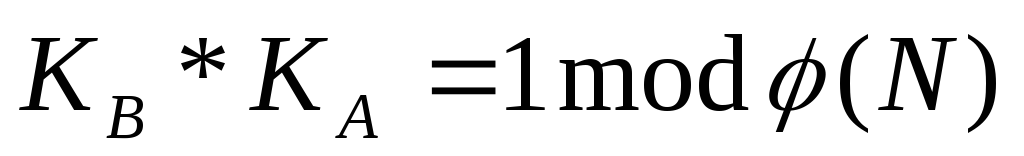, використовуючи розширений алгоритм Евкліда.

5. Користувач B пересилає незахищеним каналом користувачу A пару чисел (N, ).

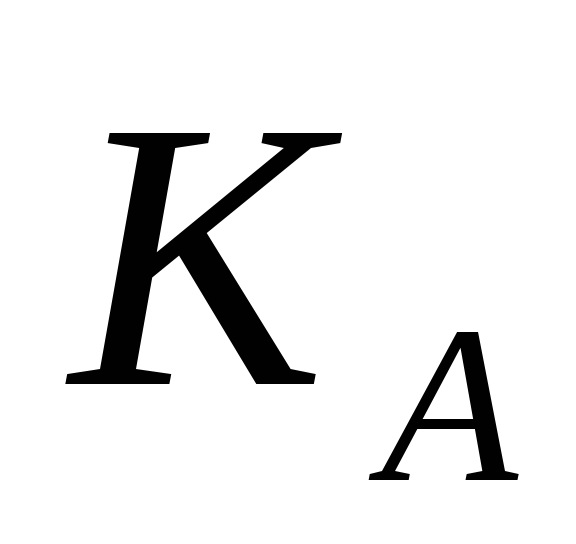Якщо користувач A має бажання передати користувачу B повідомлення М, він виконує такі кроки.

6. Користувач A розбиває вихідний відкритий текст М на блоки, кожний з яких може бути поданий у вигляді числа ,.

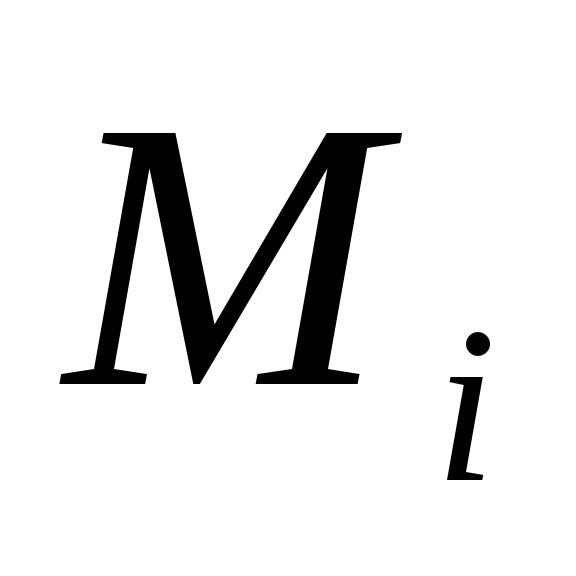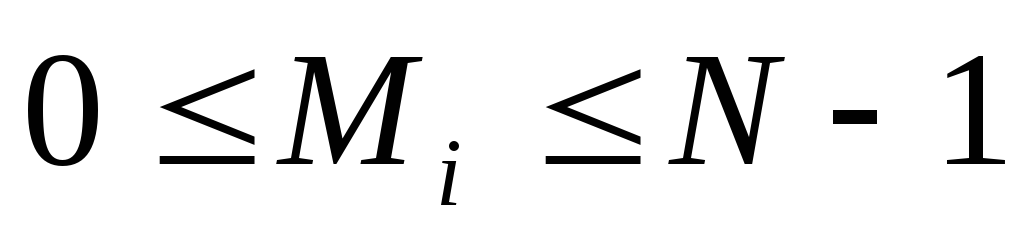7. Користувач A шифрує текст, поданий у вигляді послідовності чисел М, за формулою

і відправляє користувачеві В криптограму

.

6. Користувач B розшифровує прийняту криптограму 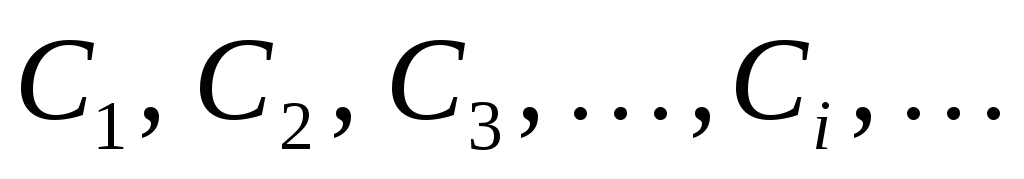, використовуючи таємний ключ 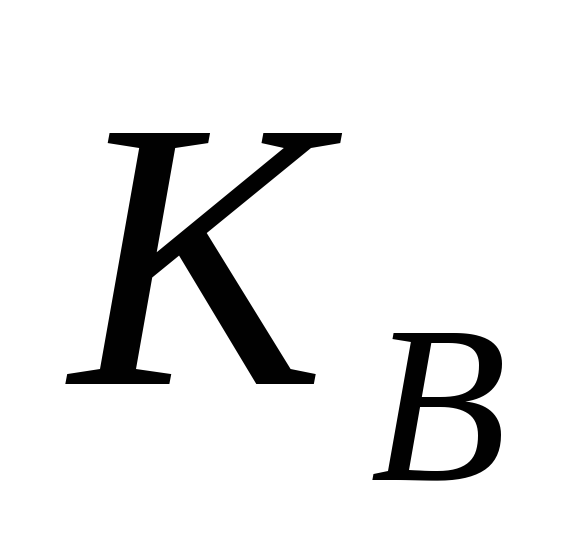, за формулою

.

У результаті буде отримана послідовність чисел , які являють собою вихідне повідомлення М. Щоб алгоритм RSA мав практичну цінність, необхідно мати можливість без істотних витрат генерувати великі прості числа, вміти оперативно обчислювати значення ключів та .

Безпека й швидкодія криптосистеми RSA

Безпека алгоритму RSA базується на труднощах розв’язання задачі факторизації великих чисел, що є добутками двох великих простих чисел. Дійсно, крипостійкість алгоритму RSA визначається тим, що після формування таємного ключа й відкритого ключа "стираються" значення простих чисел P й Q, і тоді винятково важко визначити таємний ключ за відкритим ключем, оскільки для цього необхідно розв’язати задачу знаходження дільників P та Q модуля N.

Розкладання величини N на прості множники Р і Q дозволяє обчислити функцію , а потім визначити таємне значення , використовуючи рівняння (4.8).

Іншим можливим способом криптоаналізу алгоритму RSA є безпосереднє обчислення або підбір значення функції . Якщо встановлено значення , то співмножники P й Q обчислюються досить просто. Справді, нехай

Знаючи (N), можна визначити х і потім y; знаючи х та y, можна визначити числа P і Q з таких співвідношень:

.

Однак ця атака не простіша задачі факторизації модуля N.

Задача факторизації є задачею, яка важко розв’язується для великих значень модуля N.

Спочатку автори алгоритму RSA пропонували для обчислення модуля N вибирати прості числа P й Q випадковим чином, по 50 десяткових розрядів кожне. Вважалося, що такі великі числа N дуже важко розкласти на прості множники. Один з авторів алгоритму RSA, Р.Райвест, вважав, що розкладання на прості множники числа з майже 130 десяткових цифр, наведеного в їхній публікації, зажадає більше 40 квадрильйонів років машинного часу. Однак цей прогноз не виправдався через порівняно швидкий прогрес обчислювальної потужності комп’ютерів, а також поліпшення алгоритмів факторизації.

Один з найбільш швидких алгоритмів, відомих у цей час, алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (із числом десяткових розрядів більше 120) за число кроків, оцінюваних величиною

У 1994 р. було факторизовано число з 129 десятковими цифрами. Це вдалося здійснити математикам А.Ленстра й М.Манассі за допомогою організації розподілених обчислень на 1600 комп’ютерах, об’єднаних мережею, протягом восьми місяців. На думку А.Ленстра та М.Манассі, їхня робота компрометує криптосистеми RSA і створює більшу погрозу їхнім подальшим застосуванням. Тепер розроблювачам криптоалгоритмів з відкритим ключем на базі RSA доводиться уникати застосування чисел довжиною менше 200 десяткових розрядів. Останні публікації пропонують застосовувати для цього числа довжиною не менше 300 десяткових розрядів.

Завдання|задавання| 1

Виконати шифрування і дешифровку| за наступних|слідуючих| умов: e - відкритий ключ ,d- закритий ключ _,

_{Талиця№1}

Номер варіанту	Вихідні дані
	p	q	d	M
1	5	11	3	9
3	3	11	3	8
3	5	13	3	3
4	11	13	11	6
5	7	11	7	8
6	5	11	3	9
7	7	1	17	8
8	11	13	11	7
9	17	31	7	2
10	5	11	3	3
11	5	13	5	2
12	7	11	7	3
13	11	13	11	3
14	7	13	5	3
15	3	11	3	4
16	11	13	11	5
17	11	13	11	4
18	5	13	5	7
19	7	11	7	7
20	7	11	7	5
21	11	13	11	2
22	7	11	17	3
23	7	11	17	2
24	5	13	5	5
25	3	11	3	6
26	3	11	3	5
27	5	11	3	4
28	3	11	3	8

 Завдання|задавання| 2

На підставі цих же вихідних|початкових| даних виконати шифрування і дешифровку за наступних|слідуючих| умов e - відкритий ключ ,d- закритий ключ _,

Завдання|задавання| по цифровому підпису

 Завдання|задавання| 3

Сформувати ЕЦП до повідомлення|сполучення| в стовпці (M') і відправити разом з відкритим|відчиняти| текстом одержувачеві|отримувачу|. У одержувача|отримувача| виробити|справляти| перевірку цілісності прийнятого повідомлення|сполучення|.

 Порядок|лад| виконання.

1. Сформувати профіль повідомлення|сполучення| M’ за допомогою спрощеної функції хешування – перемножування всіх цифр окрім|крім| нуля|нуль-елемента| цього повідомлення|сполучення|.

2. Створити ЕЦП шифруванням профілю повідомлення h(M’) закритим ключем відправника (D_a), тобто D_a (h(M’)).

3. Відправити M’D_a (h(M’)) одержувачеві.

4. На стороні одержувача|отримувача| сформувати профіль прийнятого повідомлення|сполучення|, тобто повторити пункт 2.

5. Створити профіль дешифровкою ЕЦП відкритим ключем відправника (E_a (D_a (h(M’)) = h(M’)).

6. Порівняти два профілі повідомлення|сполучення| M’ (пункта 4 і 5). Переконатися в їх збігу.

 Варіанти завдання|задавання|:

Таблиця №2

Номер варіанту	Вихідні дані
	p	q	d	M’
1	5	11	3	397
2	3	11	3	629
3	5	13	3	777
4	11	13	11	922
5	7	11	7	269
6	5	11	3	397
7	7	1	17	629
8	11	13	11	773
9	17	31	7	616
10	5	11	3	777
11	5	13	5	166
12	7	11	7	777
13	11	13	11	777
14	7	13	5	777
15	3	11	3	267
16	11	13	11	775
17	11	13	11	267
18	5	13	5	773
19	7	11	7	773
20	7	11	7	775
21	11	13	11	616
22	7	11	17	777
23	7	11	17	616
24	5	13	5	775
25	3	11	3	292
26	3	11	3	775
27	5	1	3	267
28	3	11	3	629

 Приклад|зразок|.

Вихідні|початкові| дані: повідомлення|сполучення| M’ = 947829 p = 7 q = 11 d = 17 (закритий|зачиняти| ключ|джерело| відправника) e = 53 (відкритий|відчиняти| ключ|джерело| відправника)

 Визначення профілю повідомлення|сполучення| M’:

Операція	Результат
Множення 9 на 4	36
Відкидання першої цифри	6
Множення 6 на 7	42
Відкидання першої цифри	2
Множення 2 на 8	16
Відкидання першої цифри	6
Множення 6 на 2	12
Відкидання першої цифри	2
Множення 2 на 9	18
Відкидання першої цифри	1

2. Формування підпису D: h(947829)= D(8)= h(947829)^d mod n = 8¹⁷(mod 77)= [(8⁵ mod 77)(8⁵ mod 77)(8⁵ mod 77)*64] mod 77 = 43³ *64 mod 77 = 57

3. Відправлення повідомлення|сполучення| з|із| цифровим підписом одержувачеві|отримувачу| (947829, 57).

Одержувач|отримувач| за допомогою відкритого|відчиняти| ключа|джерела| відправника розшифровує цифровий підпис і отримує|одержує| профіль:

E(D(h))= 57^e mod 77 ((57³ mod 77) ^17*17*57) mod 57 = (8¹⁷ mod 77 * 57 * 57) mod 57 = 57³ mod 57 = 8  

4. Одержувач|отримувач| визначає значення профілю повідомлення|сполучення|, що поступило, як показано в таблиці пункту 1, H9947829|) = 8. Оскільки|тому що| обоє|обидва| значення хэш-функции| збіглися, підпис вірний.

Виконання задач: