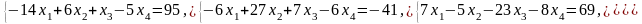Приклад розрахунків

Розв’язати СЛАР методами простої ітерації з точністю :

Сформуємо матрицю коефіцієнтів  і вектор вільних членів :

, .

Визначимо збіжність ітераційного процесу для заданої системи. Знайдемо норми матриці :

;

;

;

Таким чином, перша, друга та четверта канонічні норми менші одиниці, тому ітераційний процес для даної системи буде збіжним. Оберемо початкове наближення розв’язку: . Тобто, . Для знаходження першого наближення вектора розв’язку початкове наближення підставимо в праву частину початкової системи:

Перевіримо виконання умови закінчення ітераційного процесу:

. Умова не виконується, різниця між наближеннями більше , тому продовжимо обчислення

. Умова не виконується, тому продовжимо обчислення

. Різниця між наближеннями більше , тому продовжимо обчислення

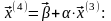
. Умова закінчення обчислень виконується, різниця між наближеннями менше . Останнє наближення приймаємо за остаточний розв’язок:

.

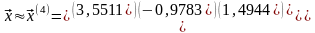Завдання

Розв’язати систему лінійних алгебраїчних рівнянь методом Зейделя, дослідити виконання умови збіжності ітераційного процесу, точність =0,001:

№	СЛАР	№	СЛАР
1.		6.
2.		7.
3.		8.
4.		9.
5.		10.

Тема 2. Нелінійні рівняння

Знаходження наближених значень дійсних коренів алгебраїчного рівняння порядку n:

(16)

або трансцендентного рівняння:

(17)

в методах обчислювальної математики виконують у два етапи:

• відокремлюють корені, тобто визначають проміжки на числовій осі Ox, на кожному з яких знаходиться єдиний (відокремлений) корінь рівняння;

• уточнюють відокремлені корені до потрібного наближення.

Метод послідовного перебору для відокремлення коренів базується на таких положеннях:

• якщо неперервна на відрізку функція приймає на його кінцях значення різних знаків (тобто ), то рівняння (16) або (17) має на цьому відрізку при наймі один корінь;

• якщо функція до того ж ще й строго монотонна, то корінь на відрізку єдиний.

Виходячи з приблизного графіка функції , визначають інтервал . Далі обчислюють значення , починаючи з точки , рухаючись управо з деяким кроком h (рис.1). Як тільки виявиться пара сусідніх значень , яка має різні знаки, і функція монотонна на цьому відрізку, так відповідні значення аргументу x (попереднє й наступне) можна вважати кінцями відрізку, що містить корінь.

Рис.2

У методі Ньютона ділянка кривої послідовно замінюється її дотичною в точці A або B (рис.2). Абсциса точки перетину дотичної з віссю 0x - буде першим наближеним значенням кореня. Щоб уточнити застосуємо метод дотичних до відрізка , отримаємо друге наближення - , і так далі. Точка, в якій будується дотична, обирається з умови співпадання знаків функції та її другої похідної .

Розрахункова формула методу Ньютона:

(18)

де , якщо ;

, якщо .

Розрахунки продовжують до виконання умови .