Заочна форма навчання алгоритми та методи обчислень контрольна робота

Тема 1. Системи лінійніх алгебраїчних рівнянь

Система лінійних алгебраїчних рівнянь із n-невідомими має вигляд:

, або

(1)

В матричній формі запишемо систему так:

,

(2)

де - дійсна матриця коефіцієнтів системи; - вектор вільних членів; - вектор невідомих.

Ефективність способів розв’язування системи (1) залежить від структури і властивостей матриці А: вимірності, обумовленості, симетричності, наповненості та особливості розташування ненульових елементів. Система (1) буде мати єдиний розв’язок, якщо матриця А невироджена, тобто .

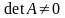Чисельні методи розв’язування СЛАР діляться на дві групи: прямі та ітераційні.

Прямі методи дозволяють за скінчену кількість дій отримати точний розв’язок системи (1), якщо елементи матриці А і вектор вільних членів задано точно, і обчислення проводяться без округлень.

Ітераційні методи дозволяють знайти наближений розв’язок шляхом побудови послідовності наближень (ітерацій): починаючи з деякого наближення .

Вибір методу розв’язування СЛАР залежить від властивостей матриці А та від характеристик комп’ютера (швидкодії, розрядної сітки, об’єму оперативної пам’яті). Прямі методи використовуються для розв’язування систем невеликої вимірності ( ). Ітераційні методи використовують зазвичай для систем великої вимірності ( ), коли використання прямих методів є недоцільним через необхідність виконувати занадто велику кількість арифметичних операцій.

Метод LU-розкладання

Якщо всі головні мінори матриці коефіцієнтів А системи (1) відмінні від нуля, то існують такі нижня L і верхня U трикутні матриці, що A=LU. Якщо елементи діагоналі однієї з матриць L або U фіксовані (ненульові), то таке розкладання буде єдиним.

Отримаємо формули для розкладання матриці А у випадку фіксування діагональних елементів нижньої трикутної матриці L.

_{, . (3)}

_, (4)

Виконавши перемноження матриць LU=A, отримаємо рівняння:

Знайдемо невідомі в такому порядку:

• з першого рядка рівнянь маємо (j=1,…,n);

• з частини рівнянь першого стовпця, що залишилася (i=2,…,n);

• з частини рівнянь другого рядка, що залишилася

(j=2,…,n);

• з частини рівнянь другого стовпця, що залишилася

(i=3,…,n);

і так далі. Останнім знайдемо елемент .

Якщо матриця А системи (1) розкладена на добуток трикутних матриць L i U, то замість системи (2) можемо записати еквівалентне рівняння:

.

Введемо допоміжний вектор змінних ., тоді перепишемо систему у вигляді Таким чином, розв’язування системи (1) звелося до послідовного розв’язання двох трикутних систем.

Запишемо рівняння у розгорнутій формі:

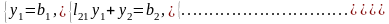(5)

Звідки знаходимо значення компонент вектора шляхом прямих підстановок:

(6)

Розгорнемо тепер рівняння :

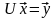(7)

Звідки знайдемо значення невідомих у зворотному порядку:

(8)

Існує ще альтернативний алгоритм LU-розкладання матриці А через операції матричного множення.

Утворимо матрицю М₁:

, де (i=2,…,n).

Помножимо матрицю А зліва на М₁, отримаємо матрицю А₁:

.

З якої утворимо матрицю М₂:

, де (i=3,…,n).

Помножимо матрицю А₁ зліва на М₂, отримаємо матрицю А₂:

.

І так далі. Остання буде матриця М_n-1:

, де .

Тоді матриця А_n-1 буде верхньою трикутною матрицею:

, тобто матрицею U. Таким чином , а нижня трикутна матриця L отримується з ненульових стовпців матриць :

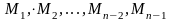, або .