Формула Байеса

Формула Байеса

9. Формула Бернулі

Якщо ймовірність  настання події  в кожному з випробувань стала, то ймовірність  того, що подія  настане  разів в  незалежних випробуваннях дорівнює

10.

11.

12.

Визначення Розподіл ймовірностей у схемі Бернулі

Дискретна випадкова величина ξ називається такою, що має розподіл Бернуллі, якщо її закон розподілу має вигляд: , де p — параметр, що визначає розподіл, .

Позначається .

Функція розподілу має вигляд:

.

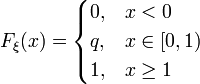Числові характеристики[ред. • ред. код]

Математичне сподівання:

Mξ=0q+1p=p.

Дисперсія:

.

Теорема Пуассона 

Пусть есть последовательность серий испытаний Бернулли. Пусть  — вероятность «успеха»,  — количество «успехов».

Тогда если

1. 

2. 

3. 

то

13 Теорема Бурнули

Формулировка Править

Рассмотрим схему Бернулли с вероятностью успеха  то есть пусть дана последовательностьнезависимых случайных величин  где

Определим  как число успехов в первых  испытаниях:

Тогда

 при 

то есть

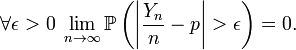
14. Проста течія подій