5.9.2. Структурный синтез автомата Мура
Выполним структурный синтез микропрограммного автомата Мура, заданного своей таблицей переходов-выходов (табл. 5.13 или табл. 5.14). В качестве примера синтез будем выполнять по обратной таблице (табл. 5.14).
В исходном автомате количество состояний М=7, следовательно число элементов памяти m = ] log 2 M [ = ] log 2 7 [ = 3. Пусть для синтеза используется D-триггеры.
Кодируем внутренние состояния автомата, используя алгоритм кодирования для D-триггеров ( чем больше переходов в это состояние, тем меньше единиц должно быть в коде этого состояния). Количество переходов в данное состояние легко определяется из обратной таблицы: a1 ~ 2, a2 ~ 3, a3 ~ 2, a4 ~ 1, a5 ~ 1, a6 ~ 1, a7 ~ 2. Поэтому коды состояний следующие:
a2 - 000, a1 - 001, a3 - 010, a7 - 100, a4 - 011, a5 - 101, a6 - 110.
Строим структурную таблицу переходов - выходов автомата Мура. Построение таблицы выполняется аналогично автомату Мили. Результат представлен в табл. 5.16.
Табл. 5.16. Структурная таблица переходов - выходов автомата Мура.
am |
K(am) |
as(Y) |
K(as) |
X |
ФВ |
a6 |
110 |
a1(-) |
001 |
|
D3 |
a7 |
100 |
|
|
1 |
D3 |
a1 |
001 |
a2(y1y2) |
000 |
|
- |
a2 |
000 |
|
|
|
|
a6 |
110 |
|
|
|
|
a1 |
001 |
a3(y3y4) |
010 |
|
D2 |
a4 |
011 |
|
|
1 |
D2 |
a3 |
010 |
a4(y1y4) |
011 |
|
D2D3 |
a2 |
000 |
a5(y2y3) |
101 |
|
D1D3 |
a2 |
000 |
a6(y4) |
110 |
|
D1D2 |
a3 |
010 |
a7(y2) |
100 |
|
D1 |
a5 |
101 |
|
|
1 |
D1 |
Выражения для функций возбуждения получаются в виде суммы произведений aiх, где ai – исходное состояние, х – условие перехода:
,
и
или,
если принять, что
,
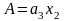и
,
,
и
Выражения для выходных сигналов автомата Мура получаем, исходя из того, что эти сигналы определяются только внутренним состоянием автомата:
,
,
и
.
Для построения функциональной схемы автомата, как и в предыдущем случае, используем дешифратор состояний. Схема представлена на рис. 5.20.
