Вихідні та розрахункові дані для перевірки математичних властивостей дисперсії

Групи господарств	Кількість господарств	Середина інтервалу хі	((xi+a)-(x+a))2∙ni a=2	(cxi-c∙x)2ni c=2	(xi-a)2ni a=26,5
25-28	11	26,5	63,36	253,44	0
28-31	10	29,5	3,6	14,4	90
31-34	2	32,5	25,92	103,68	72
34-37	2	35,5	87,12	348,48	162
Разом	25	х	180	720	324

1. δ²_xa=δ²

δ²_xa = = = 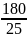7,2

2. δ²_cx= c²∙δ²

δ²_cx= 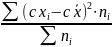= =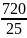28,8

4∙7,2 =28,8

3. δ²_x < δ²_a

δ²_a= = =12,96

7,2 < 12,96

4. δ²_a =0, якщо a=const

Для того щоб підтвердити правильність розрахунку дисперсії, розрахуємо її способом моментів.

Таблиця 9

Вхідні та розрахункові дані для обчислення дисперсії за урожайністю озимого ячміню способом моментів

Групи господарств	Кількість господарств	Середина інтервалу хі	x-a, a=26,5	∙ni, h=3	( )2 ∙ ni
25-28	11	26,5	0	0	0
28-31	10	29,5	3	10	10
31-34	2	32,5	6	4	8
34-37	2	35,5	8	6	18
Разом	25	х	x	x	36

Одержані дані підставимо до формули і обчислимо величину дисперсії:

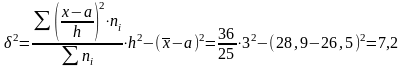
Величина дисперсії збігається, отже розрахунки вірні.

Таблиця 10

Вихідні та розрахункові дані для обчислення асиметрії та ексцесу

Групи господарств	Кількість господарств	Середина інтервалу, xi
25-28	11	26,5	-152,064	364,954
28-31	10	29,5	2,16	1,296
31-34	2	32,5	93,312	335,923
34-37	2	35,5	574,992	3794,947
Разом	25	Х	518,4	4497,12

Обчислимо асиметрію і ексцес:

центральний момент першого порядку;

центральний момент другого порядку;

центральний момент третього порядку.

= 20,736

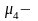центральний момент четвертого порядку.

179,885

A = = 1,074

A>0, отже маємо правосторонню асиметрію.

Е= 0,471

Е > 0, отже розподіл гостровершинний.

А=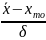 = = 0,335

А ≤ 1 і це свідчить про помірно скісний розподіл.

, 28,9 > 28,408 > 28 - правостороння асиметрія.

29