
- •Лекция № 8 Методы получения рекурсивных оценок случайных процессов
- •8.1. Сопоставление результатов выборочных и рекурсивных оценок
- •8.2. Особенность рекурсивных вычислений оценки
- •8.3. Формализованная процедура оценки случайного процесса (фильтр Калмана-Бьюси ─ фкб)
- •8.3.1. Аналоговые алгоритмы фкб
- •8.3.2. Особенность оценивания случайных величин
- •8.4. Цифровые алгоритмы фкб
- •8.4.1. Особенности функционирования цифровых фкб
- •8.4.2. Режимы фкб
- •8.5. Оценки состояния в многомерных системах
- •8.5.1. Многомерные модели состояния случайных процессов
- •8.5.2. Многомерные модели наблюдений случайных процессов
- •8.5.3. Особенность функционирования дискретных многомерных фкб
- •8.6. Особенность оценки дискретных случайных величин
- •Контрольные вопросы
8.5.2. Многомерные модели наблюдений случайных процессов
Взаимная связь между компонентами и может образоваться также при измерениях. Так, при измерении может оказаться, что наряду с основным измерением появляются те или иные доли других компонент. В этом случае уравнение наблюдения для компоненты принимает вид:
 .
.
Таким образом матрица в уравнении наблюдения становится полной и уравнения наблюдений между собой связаны:
 (8.22)
(8.22)
Часто эти связи несут отрицательный характер, не позволяют выделить тот или иной процесс в чистом виде.
Аналогичный
(8.22) вид имеют уравнения для наблюдаемых
сигналов, используемых в беспроводных
технологиях WiFi,
WiMAX
где применяется многомерное
пространственно-временное кодирование,
известное под аббревиатурой MIMO.
Вместе с тем, при наличии перекрестных
связей в уравнении наблюдения (8.22) не
добавляет интегральных свойств в системе
 .
Скорее эти перекрестные связи носят
характер взаимных помех, с которыми
часто приходится бороться или их
компенсировать.
.
Скорее эти перекрестные связи носят
характер взаимных помех, с которыми
часто приходится бороться или их
компенсировать.
Таким
образом, имеется возможность учета
взаимных связей между компонентами
многомерной системы за счет трех
различных механизмов: за счет коэффициентов
состояния
,
коэффициентов генерации
и за счет взаимных влияний при измерениях
 .
При этом может действовать какой-либо
один из упомянутых механизмов или
проявляться совместно с другими. Выбор
того или иного представления определяет
исследователь в зависимости от контекста,
смысла и удобства операций в решаемой
задаче.
.
При этом может действовать какой-либо
один из упомянутых механизмов или
проявляться совместно с другими. Выбор
того или иного представления определяет
исследователь в зависимости от контекста,
смысла и удобства операций в решаемой
задаче.
8.5.3. Особенность функционирования дискретных многомерных фкб
Отличительной
особенностью многомерных (векторных)
ФКБ в том, что матрицы
 и
и
 имеют не только диагональные элементы
имеют не только диагональные элементы
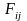 и
и
 ,
определяющие собственно свойства
-го
состояния
,
но и недиагональные
и
,
позволяющие учитывать взаимную корреляцию
между
и
компонентами.
,
определяющие собственно свойства
-го
состояния
,
но и недиагональные
и
,
позволяющие учитывать взаимную корреляцию
между
и
компонентами.
Алгоритм многомерного ФКБ (8.16) должен соответствовать многомерной модели состояния (8.20). При этом может использоваться модель с обоими полными матрицами и , или же одна из них может быть диагональной, а другая полная. Представим аналитический вид двумерного уравнения состояния с двумя полными матрицами состояния и генерации.
 (8.23)
(8.23)
Представим
алгоритм оценки компонент двумерного
ФКБ, связь между компонентами
 и
и
 которого, осуществляется только за счет
которого, осуществляется только за счет
 ,
,
 .
.
 (8.24)
(8.24)
Структурная схема алгоритма ФКБ, соответствующего (8.24) представлена на рис.8.8.

Рис. 8.8. Структурная схема двумерного ФКБ
Структурная
схема двумерного ФКБ может иметь и иной
вид. Очевидно связь между компонентами
можно также учесть и за счет
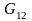 и
и
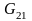 ,
исключив элементы
и
.
При полных матрицах
,
исключив элементы
и
.
При полных матрицах
 и
и
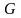 появляются еще и связующие элементы
появляются еще и связующие элементы
 и
и
 .
Если же взаимные влияния моделируются
лишь за счет элементов матрицы
.
Если же взаимные влияния моделируются
лишь за счет элементов матрицы
 ,
то взаимные связи в ФКБ учитываются в
коэффициентах
,
то взаимные связи в ФКБ учитываются в
коэффициентах
 .
.
Пренебрежение взаимными связями приводит к потере качества оценок, а соответственно и управления, ибо этим самым игнорируются наиболее важные системные свойства целостности и эмерджентности.
