8.3. Формализованная процедура оценки случайного процесса (фильтр Калмана-Бьюси ─ фкб)

Данная процедура может иметь как аналоговый, так и дискретный вид в зависимости от того, каким образом представлен процесс . Как в том, так и в ином случае для оценки используют три (триаду) уравнения, достаточных для синтеза алгоритма оценки этого процесса. Три уравнения: наблюдения, состояния и оценки в классическом ФКБ представлены линейными уравнениями и имеют замкнутый, завершенный вид. Однако во многих случаях уравнения наблюдения или состояния этого процесса могут оказаться нелинейными, включать в себя тригонометрические функции, квадраты состояний или иные нелинейные выражения. Задача оценки при наличии нелинейности усложняется, решения находятся через процедуры упрощения, линеаризации или другие приемы, приводящие к тем или иным приближениям. Теория, посвященная синтезу таких нелинейных алгоритмов, носит название теории марковской нелинейной фильтрации.

В данной дисциплине рассматриваются только линейные процедуры, к которым, в основном, и удается свести практические задачи, возникающие в ТКС.

8.3.1. Аналоговые алгоритмы фкб

Триада уравнений для алгоритма оценки случайного процесса :

1. Уравнение наблюдения:

. (8.7)

2. Уравнение состояния:

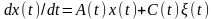. (8.8)

3. Уравнение оценки, удовлетворяющей критерию МСКО:

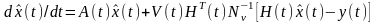, (8.9)

где 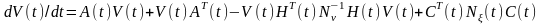- (8.10)

дифференциальное уравнение Риккати для апостериорной дисперсии ошибки оценки.

- спектральные плотности мощности соответственно шума генерации в модели состояния и шума наблюдения в уравнении наблюдения. Если первый шум 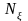- носит виртуальный характер, он определяет уровень процесса , то - отображает реальный шум в канале наблюдения.

Все уравнения (8.7) - (8.10) представлены в виде многомерных функций с коэффициентами матричного вида, содержащих транспонирование, обозначаемое (Т) и обратные матрицы со степенями (-1).

Из сопоставления уравнений состояния (8.8) и оценки (8.9) видно, что левые части и первые слагаемые правых частей уравнений совпадают. Второе слагаемое правой части в квадратных скобках носит название невязки: . Очевидно, если оценка 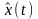и оцениваемый случайный процесс совпадают , то невязка 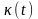близка к нулю (это бывает при малых значениях шума наблюдения ), при этом корректировать оценку - не надо. Если же имеет место отклонение от оцениваемого значения того или иного знака , то, соответственно, невязка возрастает, и является корректирующим сигналом для получения новой оценки.

Из уравнения оценки (8.9) видно, что невязка умножается на величину, обратную спектральной плотности мощности шума наблюдения . Очевидно, при больших уровнях этого шума величина 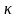(его спектральная плотность мощности) будет пропорциональна не только отклонению оценки от истинного значения, но и значению шума наблюдения. Поэтому умножение на обратную величину (при большом уровне шума наблюдения) как бы снижает доверие к невязке, и таким образом доля вклада второго слагаемого в (8.9) уменьшается. При этом можно утверждать, что при качественных измерениях, когда шум , основной вклад в формирование оценки дает 2-е слагаемое, при некачественных – первое.

Важную роль также играет умножение невязки на функцию , определяющую изменение апостериорной дисперсии ошибки оценки. Анализ показывает, что сразу после включения ФКБ значения вначале относительно велики, затем постепенно уменьшаются до определенного уровня . Значение можно вычислить из уравнения (8.10), приравняв к нулю 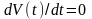, то есть определить апостериорную дисперсию в установившемся состоянии фильтра, или, что тоже самое: определить точность оценки в этом установившемся состоянии.

При из (8.10) получаем обыкновенное квадратное уравнение, одно из решений которого позволяет определить искомую дисперсию. Так, полагая, что 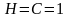, - мощность шума, - спектральная плотность мощности чисто случайного полезного оцениваемого сигнала, из (6.9) получаем:

, (8.11)

где - отношение мощности полезного сигнала к мощности шума в полосе приема этого сигнала 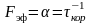. График функции (8.11) представлен на рис.8.1. Отношение апостериорной дисперсии к априорной 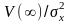всегда <1, если процедура ФКБ – устойчива.

Рис.8.1. График изменения абсолютного и относительного значения апостериорной дисперсии от 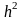-уровня сигнал/шум

Из рис.8.1. следует, что значение относительной апостериорной дисперсии монотонно уменьшается (соответственно относительная точность оценки возрастает) по мере увеличения отношения сигнал/шум. В тоже время из (8.11) также следует, что абсолютное значение апостериорной дисперсии растет пропорционально оцениваемому сигналу (см. рис.8.1). Поэтому утверждение о том, что при увеличении уровня оцениваемого сигнала точность его оценки возрастает, не верна. Верно то, что увеличивается относительная точность, но не абсолютная.

Функция в ФКБ, показывающая точность оценки, играет также другую важную роль, обеспечивая устойчивость процедуры оценки. Кроме того, из уравнения (8.11) следует, что не зависит от текущих значений оцениваемого сигнала . Таким образом, точность оценки теоретически можно вычислить априори. Однако на практике точность оценки зависит также и от того, насколько точно заданы параметры в уравнениях состояния, наблюдения и насколько удачно выбран шаг квантования в дискретных процедурах. Об этом информация – ниже.

Структурная схема модели наблюдения и ФКБ представлена на рис.8.2.

Рис.8.2. Структурная схема ФКБ. Точка над 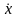означает производную

Невязка формируется на выход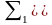е . На выходе 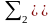имеем производную оценки . После интегратора получаем искомую оценку .

Аналоговые ФКБ легко реализуются на сосредоточенных элементах аналоговой электронной техники и по-сути представляют собой фильтр нижних частот или полосовой фильтр. Однако из-за разброса параметров они не нашли применения на практике.