Д ля двухфакторной регрессии:

na₀ +(Σx₁) a₁+(Σx₂) a₂=Σy

(Σx₁) a₀+(Σx₁²) a₁+(Σx₁·x₂) a₂=Σyx₁

(Σx₂) a₀ +(Σx₁·x₂) a₁+(Σx₂²) a₂=Σyx₂

Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.

Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:

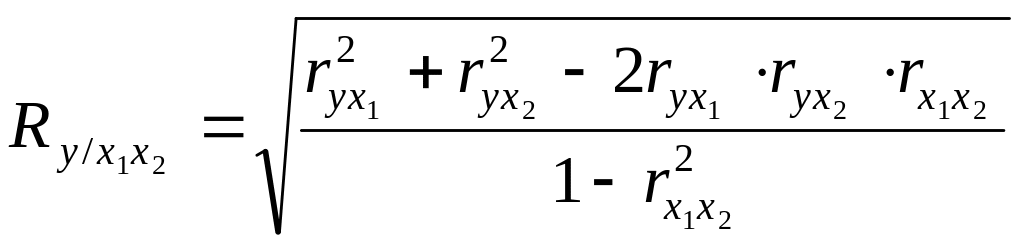
где - парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

Приближение к единице свидетельствует о сильной зависимости между признаками.

8.2. Основные этапы причинного (каузального) прогнозирования:

1. Установление степени связи между факторными и результативным признаками (расчет коэффициента корреляции).

2. Выбор факторных признаков, имеющих сильное влияние на результативный признак (там где r>0,7)/

3. Построение причинных связей (построение регрессионной модели)

4. Прогнозирование значений факторных признаков (с помощью трендовых моделей -

5. Прогнозирование значений результативного признака.

6. Определение абсолютной среднеквадратической ошибки уравнения регрессии и границ доверительного интервала:

для однофакторной модели:

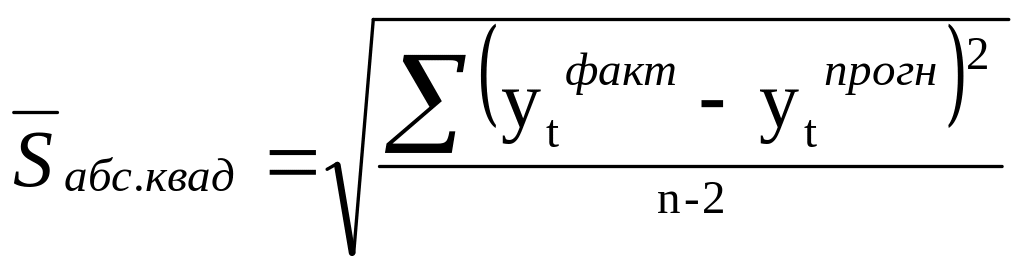
для двухфакторной модели:

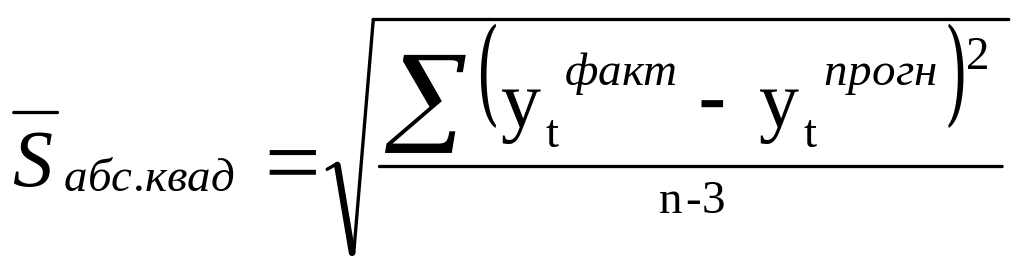
Пример:

Менеджер по сдаче жилья в аренду считает, что спрос на квартиры может быть соотнесен с числом рекламных объявлений в газетах в течении прошлых месяцев. Он собрал данные, показанные в таблицы ниже.

●●●●●

1) найдите линейный коэффициент корреляции модели и сделать вывод о степени связи между факторным и результативным признаками;

2) определите уравнение регрессии методом наименьших квадратов;

3) определите число сданного жилья, если в прошлом месяце было 20 рекламных объявлений;

4) сколько жилья будет сдано при отсутствия рекламных объявлений?

5) сколько рекламных объявлений необходимо поместить в этом месяце, чтобы спрос на квартиры составил 50?

6) найдите доверительный интервал прогноза.

Решение

1. Рассчитываем линейный коэффициент корреляции. Расчеты проводятся с помощью следующей таблицы 3.

Таблица 3

Расчет коэффициента корреляции

Жилье (квартиры), у	Реклама в газетах, х	х•у	х2	у2
15	7	105	49	225
9	4	36	16	81
40	16	640	256	1600
20	7	140	49	400
25	13	325	169	625
25	9	225	81	625
15	10	150	100	225
35	16	560	250	1225
30	14	420	196	900
Сумма: 214	96	2601	1172	5906

Вывод:

r>0,7

- Сильная связь между факторным и результативным признаками