Тема 4. Параметрические критерии различий

1. Алгоритмы параметрических критериев.

Параметрические критерии применяются для выборок с нормальным законом распределения. Формула расчета этих критериев содержат параметры выборки: среднее, дисперсии и др. Поэтому они называются параметрическими. Нормальность закона распределения должна быть статистически доказана с помощью одного из критериев согласия: критерий Пирсона, F-критерия Фишера, -критерия Колмогорова и др.

В ряде случаев параметрические критерии мощнее непараметрических критериев. У последних выше вероятность возникновения ошибки второго рода – принятия ложной нулевой гипотезы.

К параметрическим методам относятся следующие:

– Критерий Стьюдента

– Критерий Фишера

– Методы однофакторного анализа

– Методы двухфакторного анализа

4.2.Критерий Стьюдента

Критерий позволяет оценивать различия средних значений выборок, имеющих нормальное распределение.

Описание критерия.

Критерий применим для сравнения средних значений двух выборок полученных до и после воздействия некоторого фактора.

Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (а руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в журнале «Биометрика» под псевдонимом «Student» (Студент). Зависимые(связанные) и независимые (несвязанные) выборки При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок: пары близнецов, два измерения какого-либо признака до и после экспериментального воздействия, мужья и жёны и т. п. В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например: мужчины и женщины, психологи и математики. Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.

4.2.1.Двухвыборочный t-критерий для независимых выборок

Для двух несвязанных выборок(наблюдения не относятся к одной и той же группе объектов ) возможны два варианта расчета:

• когда дисперсии известны

• когда дисперсии неизвестны, но равны друг другу.

1. Предварительно проверяется нормальность закона распределения по одному из критериев согласия.

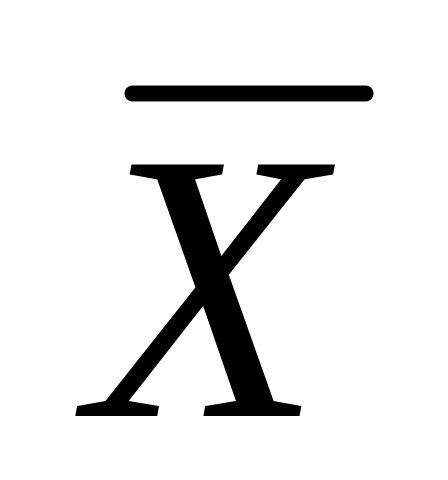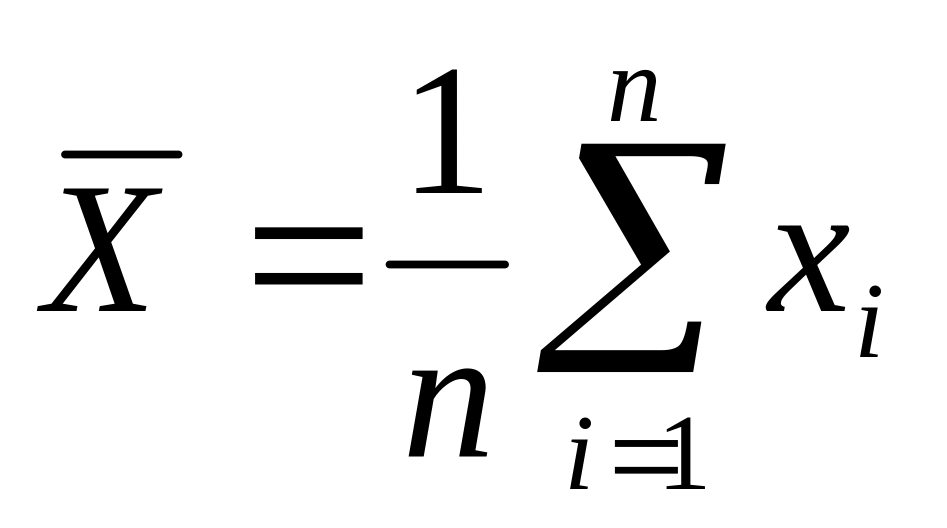2. Рассчитывается средне арифметические значения и для каждой выборки по формуле где 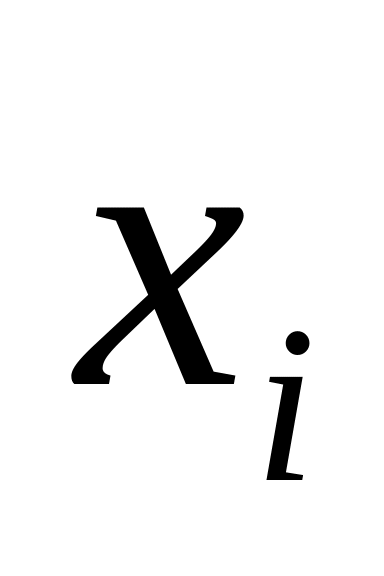– значение i-го результата наблюдения.

3. Рассчитывается - эмпирическое значение критерия Стьюдента:

Где

квадратичного отклонения. Здесь и – оценки дисперсий.

Рассмотрим сначала равночисленные выборки . В этом случае

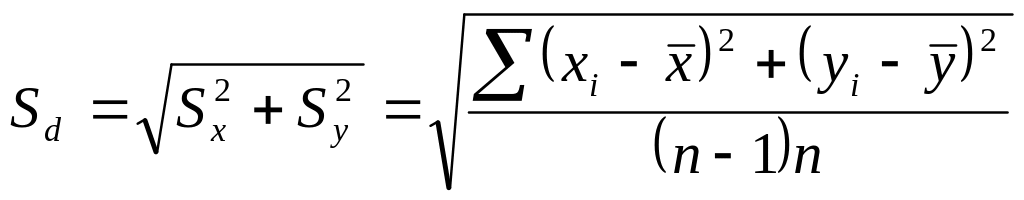
В случае наравночисленных выборок , выражение

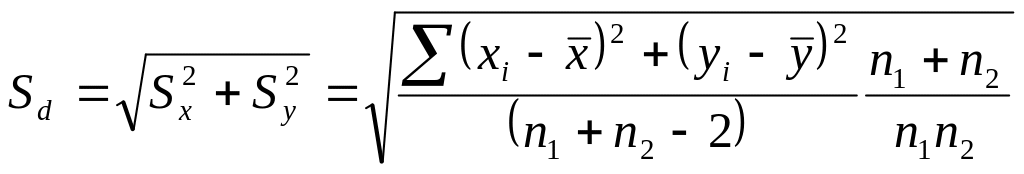
В обоих случаев подсчет числа степеней свободы осуществляется по формулам

Понятно, что при численном равенстве выборок

4. Эмпирическое значение критерия Стьюдента сравнивается с критическим значением (по таблице 1 приложения) для данного числа степеней свободы.

Нулевая гипотеза при заданном уровне значимости принимается, если эмпирическое значение .

Пример.

Психолог измерял время сложной сенсомоторной реакции выбора (в мс) в контрольной и экспериментальных группах. В экспериментальную группу (Х) входило 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающиеся спортом. Психолог приверяет гипотезу о том , что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем та же величина у людей, не занимающихся спортом.

№	Группы		Отклонения от среднего		Квадраты отклонений
	X	Y
1	504	580	-22	-58	484	3368
2	560	692	34	54	1156	2916
3	420	700	-106	62	11236	3844
4	600	621	74	-17	5476	289
5	580	640	54	-2	2916	4
6	530	561	4	-77	16	5929
7	490	680	-36	42	1296	1764
8	580	630	54	-8	2916	64
9	470	-	-56	-	3136	-
Сумма	4734	5104	0	0	28632	18174
Среднее	526	638

Cредне арифметические значения X и У: , в контрольной группе .

Тогда

Число степеней свободы k=9+8-2=15

По таблице приложения для данного числа степеней находим

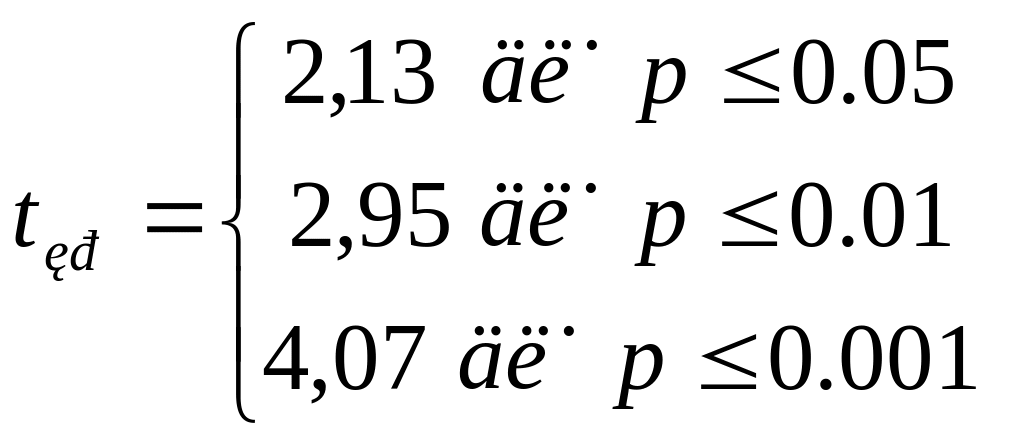
Строим ось значимости

Зона неопределенности

Зона незначимости

Зона значимости

Т.о. обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,1% уровне или иначе говоря средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше чем в группе людей активно не занимающихся спортом.

В терминах статистических гипотез это утверждение звучит так : гипотеза Н0 о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза Н1 – о различии между экспериментальной и контрольной группой.

4.2.2. Двухвыборочный t-критерий для зависимых(связанных) выборок

Под связанными выборками понимаются наблюдения для одной группы объектов, причем все наблюдения попарно связаны с каждый объектом исследования и характеризуют его состояние до воздействия и после воздействия некоторого фактора.

Гипотезы

: среднее значение в выборке не отличается от нуля.

: среднее значение в выборке отличается от нуля.

Данные в выборке измерены по шкале интервалов или по шкале отношений Сравниваемые данные должны иметь нормальный закон распределения Сравниваемых выборок две для оной группы объектов наблюдения, причем имеет место парность наблюдений в выборках.

1. Предварительно проверяется нормальность закона распределения по одному из критериев согласия.

2. Рассчитывается (i=1..n) – попарные разности вариант, и результаты измерений для i-го объекта до и после воздействия некоторого фактора. Величину 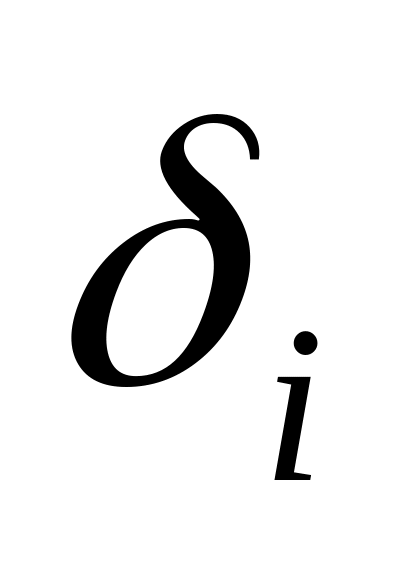будем считать независимой для разных объектов и нормально распределенной

3. Рассчитываются (лучше в табличной форме): сумма попарных разностей и вспомогательные параметры и .

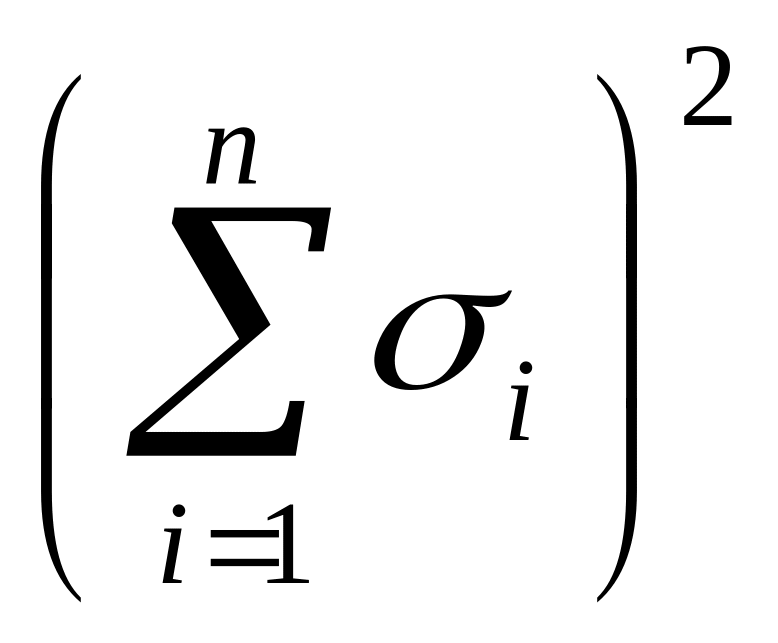4. Рассчитывается - эмпирическое значение критерия степенями свободы по формуле

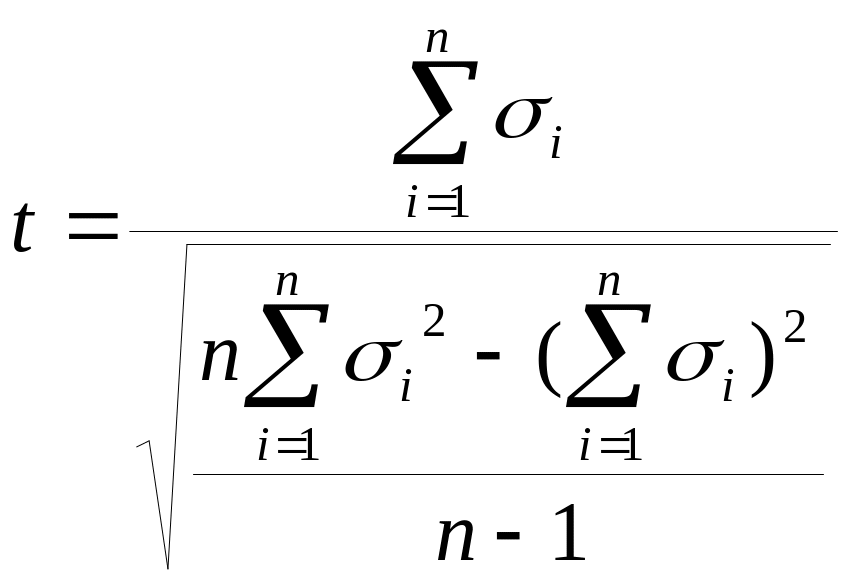
Где n – численность выборки.

5.Найденное эмпирическое значение критерия Стьюдента сравнивается с критическим значением (по таблице 1 приложения) для данного числа степеней свободы.

Нулевая гипотеза при заданном уровне значимости принимается, если эмпирическое значение .

Критическое значение для выбранной вероятности и заданного числа степеней свободы можно найти по встроенной в Excel функции СТЬЮДРАСПОБР.

Пример.

Психолог предположил, что в результате тренировки, время решения эквивалентных задач (т.е. имеющих один и тот же алгоритм решения ) будет значительно уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задачи.

Решение задачи представим в таблице.

Номер испытуемого	1 задача	3 задача
1	4,0	3,0	1	10
2	3,5	3,0	0,5	0,25
3	4,1	3,8	0,3	0,09
4	5,5	2,1	3,4	11,56
5	4,6	4,9	-0,3	0,09
6	6,0	5,3	0,7	0,49
7	5,1	3,1	2,0	4
8	4,3	27	1,6	2,56
Суммы	37,1	27,9	9,2	20,04

Число степеней свободы =8-1=7. По таблице Приложения находим