§ 29. Інтеграл Фур’є

При вивченні хвильових рівнянь виникла необхідність розкладати функції в ряди Фур’є. Інтегрування рівнянь теплопровідності вимагають в ряді випадків використання інтегралів Фур’є, які можна розглядати як певне узагальнення рядів Фур’є.

Відомо, що всяку періодичну функцію f(x) яка задовольняє умови Діріхле¹, можна подати тригонометричним рядом Фур’є:

, (1)

де коефіцієнти ряду виражаються формулами

. (2)

Ряд Фур’є (1) можна розглядати як формулу для розкладання періодичної функції (період дорівнює 2l) на гармонічні компоненти (на суму гармонік), частоти яких становлять дискретну сукупність значень .

Інтеграл Фур’є є формулою для розкладання неперіодичної функції на гармонічні компоненти з неперервною сукупністю частот. А саме, якщо функція задовольняє на кожному скінченному відрізку умови Діріхле і абсолютно інтегрована, тобто інтеграл дорівнює скінченному числу, то є справедливою рівність

, (3)

де коефіцієнти дорівнюють (4)

. (5)

Порівняння цих формул доводить, що інтеграл Фур’є (3) є узагальненням ряду Фур’є (1). У випадку інтеграла Фур’є (3) частота набуває неперервних значень від 0 до . Інтеграл Фур’є найчастіше подають в більш компактній формі

. (6)

На закінчення зауважимо, що оскільки ) парна функція відносно , розклад функції в інтеграл Фур’є (6) можна подати так:

, (7)

або , (8)

де . (9)

§ 30. Поширення теплоти в безмежному стержні

1. Розглянемо задачу про поширення теплоти в безмежному стержні (абсциса лівого кінця стержня , правого ), коли температура задовольняє диференціальне рівняння

(1)

і початкову умову . (2)

Задачі такого роду (без крайових умов) називають, як відомо, задачами з початковими умовами або задачами Коші. Сформульована задача має таке практичне значення: характеризує температуру середньої частини досить довгого стержня протягом деякого проміжку часу (доки температурні умови на кінцях стержня не впливають на розподіл температури в середній його частині).

Шукатимемо розв’язок задачі методом відокремлення змінних Фур’є. Беремо

(3)

і підставимо це значення в (1); дістанемо , звідки

. (4)

Тут спільне значення двох відношень стале, тому що перше з них не залежить від х, а друге від ;сталу позначено через . З (4) знаходимо , звідки , або

(5)

(для константи матимемо і тоді при , що фізично неможливо). З (4) також маємо , звідки

. (6)

Підставляючи (5) і (6) в (3), знаходимо

,

або

. (7)

Ми знайшли частинний розв’язок рівняння (1). Функція (7) задовольняє рівняння (1) при будь-якому дійсному . Для кожного константи і можна добирати довільно. Тому і можуть бути довільними функціями , . Так дістаємо частинні розв’язки рівняння (1) у вигляді:

. (8)

Параметр може набирати будь-які дійсні значення з інтервалу .

Оскільки рівняння (1) однорідне і лінійне, його задовольняє також сума частинних розв’язків: Тому беремо

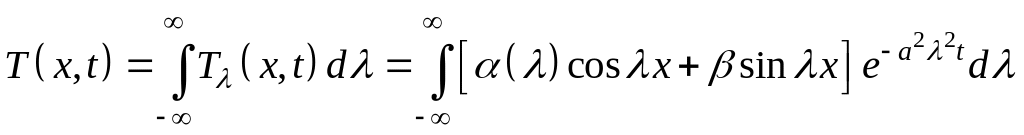. (9)

Тепер залишається визначити коефіцієнти α і β так, щоб задовольнялась початкова умова (2):

. (10)

Цю рівність можна розглядати як інтеграл Фур’є (8.8) функції . Коефіцієнти Фур’є за формулами (9) дорівнюють

, (11)

. (12)

Підставляючи і в (9), знайдемо температуру стержня

,

або ,

нарешті, змінюючи порядок інтегрування, знаходимо

. (13)

Внутрішній інтеграл формули (22) обчислюється методом диференціювання по параметру так. Здійснимо заміну змінної на нову змінну за формулою (14) і введемо для скорочення параметр :

. (15)

Маємо . (16)

Щоб обчислити інтеграл (17), знайдемо похідну по параметру :

і перетворимо, інтегруючи частинами ,

.

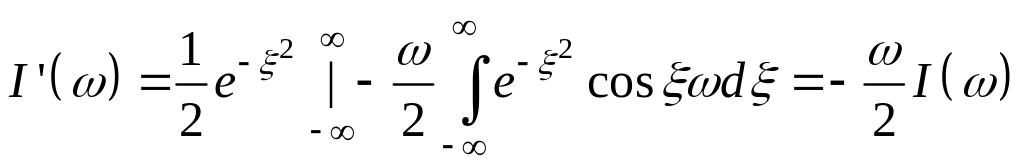Тут маємо диференціальне рівняння , звідки, інтегруючи його, , і тому

(18)

Але за формулою (17) І(0) є відомий з математичного аналізу інтеграл Пуассона, який дорівнює : (19.) З (19) та (18) маємо . Формула (18) остаточно така:

. (19)

На підставі (17) і (19) інтеграл (16) дорівнює , або, переписуючи в старих змінних,

. (21)

Підставляючи інтеграл (21) в (13), знайдемо остаточну формулу для температури стержня

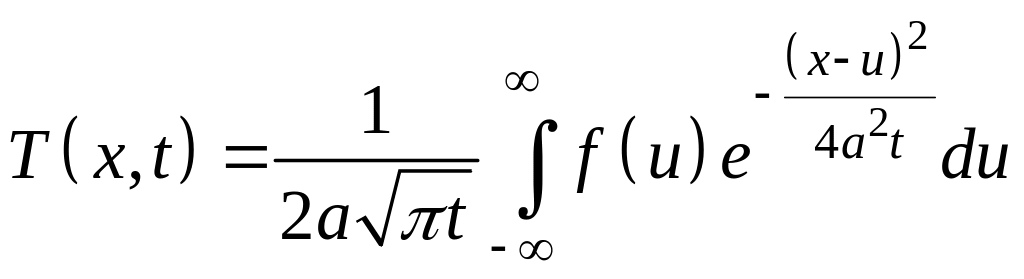. (22)

Можна прямою перевіркою переконатись e, тому, що функція (22) дійсно задовольняє як диференціальне рівняння задач (1), так і крайову умову (2).

2. Фундаментальний розв’язок рівняння теплопровідності і його фізичний зміст. Щоб з’ясувати фізичний зміст розв’язку (22), розглянемо спочатку окремий випадок. Нехай температура в початковий момент дорівнює нулю скрізь на стержні, крім інтервалу довжиною , а на цьому інтервалі нехай вона дорівнює сталій (див. рис.).

Т акий ступінчастий розподіл температури можна дістати, якщо до стержня, температура якого на початку скрізь дорівнювала нулю, підвести на інтервалі потрібну кількість тепла (піднести високотемпературне полум’я на цьому інтервалі), а саме:

(23),

де - об’єм елемента, - його маса, с - питома теплоємкість матеріалу стержня. Температуру стержня в довільній точці х в момент і знайдемо за формулою (22)

.

Застосовуючи теорему про середнє значення, матимемо

.

де — певна точка з інтервалу інтегрування .

Цю формулу можна на підставі (23) переписати у вигляді

. (24)

Значення початкової температури Т_о можна вибрати довільно. Стандартизуємо розглядуваний окремий випадок так, щоб площа ступеньки дорівнювала одиниці, тобто нехай (це означає, якщо інтервал має 2 ε одиниць довжини, то температура дорівнює градусів). При такому виборі початкової температури (або ) і формула (24) остаточно така:

. (25)

Знайдена функція визначає температуру в довільній точці х стержня в довільний момент , якщо в початковий момент вона дорівнювала нулю скрізь, крім інтервалу , в точках якого її стале значення було градусів. Такий початковий розподіл температури називають фізичним тепловим імпульсом. Отже, формула (25) визначає розподіл температури в стержні, що відповідає фізичному тепловому імпульсу одиничної інтенсивності.

Ф ормула (25) справедлива, яким би малим не було . Якщо , матимемо (добуток залишається при граничному переході незмінним і постійно дорівнює одиниці), і тому з формули (25) при знаходимо

. (26)

Тут ми позначили температуру буквою . Функцію називають фундаментальним розв’язком рівняння теплопровідності (параметр може мати довільне дійсне значення). Фундаментальному розв’язку (26) відповідає «точковий» тепловий імпульс одиничної інтенсивності. Отже, фундаментальний розв’язок рівняння теплопровідності має важливий фізичний зміст: він характеризує розподіл температури в стержні (в довільній точці х в будь-який момент ), якщо в початковий момент існував точковий тепловий імпульс одиничної інтенсивності в точці .

Точковий тепловий імпульс є, звичайно, науковою абстракцією. Його можна реалізувати більш-менш точно як фізичний імпульс на дуже малому інтервалі ( ); правда, практично розподіл температури не буде повністю ступінчастим; він виявляється неперервним, близьким до ступінчастого. Для подібних теоретичних побудов можливість абсолютно точної практичної реалізації розглядуваних абстракцій зовсім не обов’язкова.

Цікаво відмітити ряд властивостей закону розподілу температури, що відповідає фундаментальному розв’язку :

1) графік температури (26) симетричний відносно точки прикладання теплового імпульсу ; максимального значення температура досягає в точці , де вона дорівнює . Нарис. показано графік кривої 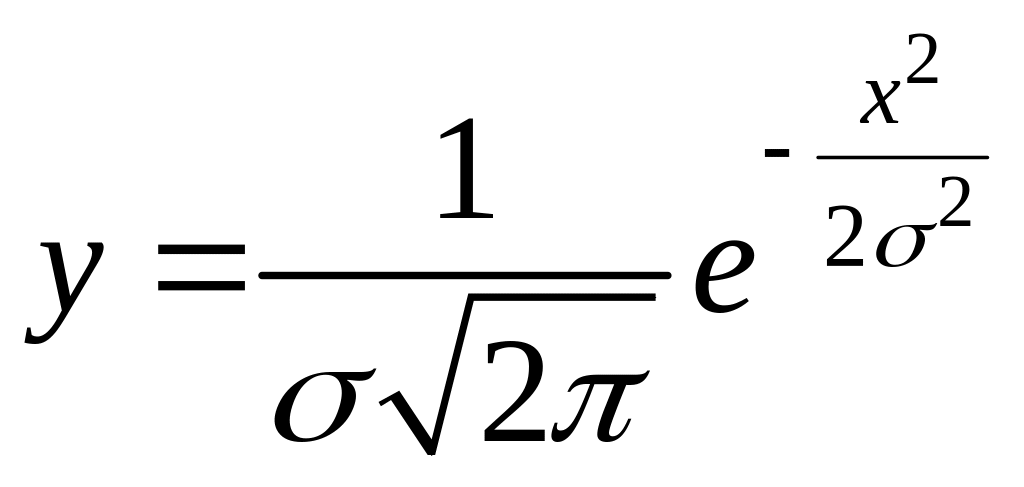, хід якої аналогічний (26);

2) площа під кривою дорівнює одиниці. Справді, ця площа виражається інтегралом

,

який після заміни змінної набирає вигляду інтеграла Пуассона . Щоб з’ясувати фізичний зміст цього факту, обчислимо теплову енергію стержня (тобто зміну енергії при переході від стану до стану ); маємо

.

Як показано, інтеграл для будь-якого моменту дорівнює одиниці, і тому

.

Отже, сталість площі під кривою температури (площа дорівнює одиниці) означає, що кількість теплової енергії, яку в момент передано стержню в певній його точці, залишається з часом в цілому незмінною (в довільний момент енергії розподілена по всьому стержню). Це й зрозуміло: бічна поверхня стержня має теплову ізоляцію.

3) У кожній фіксованій точці температура спочатку зростає від 0 при до деякого максимального значення, а потім монотонно зменшується і наближується до нуля . Застосовуючи правило Лопіталя, можна довести, що

.

При закінченні з’ясуємо фізичний зміст розв’язку (22) задачі про поширення теплоти в безмежному стержні. Його можна розглядати як суперпозицію (накладання) температур, що виникають в точці в момент внаслідок неперервного розподілу по стержню теплових імпульсів інтенсивності (на інтервалі ) , прикладених в момент .