§26. Задача Коші. Метод Даламбера розв’язування задачі Коші (метод біжучих хвиль)

Розглянемо задачу про коливання нескінченної струни:

; ; . (1)

Цю задачу – її називають задачею Коші (задача з початковими умовами) – можна тлумачити як таку, що визначає закон коливання середньої частини достатньо довгої струни, якщо нехтувати впливом кінцевих її точок (нехтувати хвилями, що відбиваються від кінців і йдуть до середини струни). Оскільки в ідеалізованій постановці задачі кінцеві точки струни зовсім відсутні (струна вважається нескінченною), то відсутні також і крайові умови.

Можна довести, що задача Коші (1) має розв’язок і єдиний, якщо – двічі диференційована функція, а – диференційована один раз.

Щоб знайти загальний розв’язок диференційного рівняння (1), здійснимо перехід від незалежних змінних до нових незалежних змінних , за формулами:

; . (2)

Після такої заміни функція буде залежати вже від змінних , . Обчислюємо похідні в рівнянні (1):

, (3)

. (4)

Аналогічно знаходимо для : ,

. (5)

Підставляючи (4) і (5) в (1), отримаємо рівняння коливань струни в нових змінних: . (6)

Це рівняння легко інтегрується. Перепишемо його в вигляді: . Інтегруючи, маємо , де - довільна функція. Повторне інтегрування дає:

, (7)

де - нова довільна функція. Повертаючись до вихідних незалежних змінних і , подамо (7) у вигляді:

. (8)

Ми знайшли загальний розв’язок рівняння (1). Довільність функцій і показує, що струна може здійснювати коливання різноманітного характеру. В кожному конкретному випадку функції і визначаються з початкових умов, тобто залежно від функцій та в (1). Для з’ясування фізичного змісту аргументів функцій і розглянемо одну функцію

. (9)

Зміщення точки від положення рівноваги при дорівнює .

Якщо, починаючи від моменту , зміщуючись від точки в напрямку вісі за законом , тобто з сталою швидкістю , то відповідно до (9) відхилення точки струни буде незмінним. Оскільки довільне, відхилення всіх точок ніби зміщуються вздовж осі з сталою швидкістю . Інакше, зсувається в напрямі вісі весь профіль струни. При цьому точки, струни не рухаються в напрямі вісі , а коливаються перпендикулярно до вісі . Ми маємо поперечну хвилю, яка поширюється в напрямі вісі з швидкістю ; аналогічно описує хвилю, що поширюється в протилежному напрямі.

Знайдемо тепер функції та залежно від функцій та , які задані за початковими умовами руху. За формулами (8), використовуючи початкові умови (1), отримаємо:

. (10)

Друге рівняння (10) проінтегруємо:

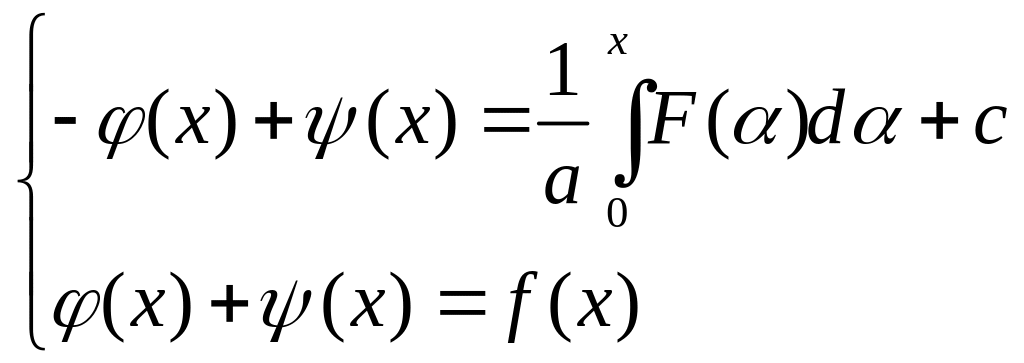. (11)

Віднімаючи та додаючи рівняння (11), знайдемо

; ; (12)

Простою заміною аргументу в функцію на , а в на знаходимо:

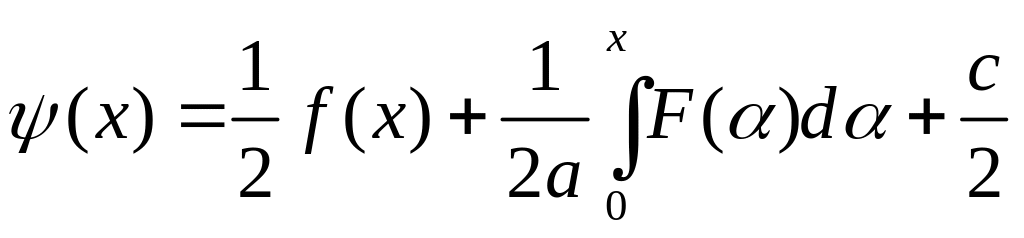; . (13)

Додаючи ці функції і об’єднуючи з інтегралами в (1), матимемо на підставі (8):

. (14)

Формула (14) є розв’язком Даламбера задачі Коші для рівняння вільних коливань струни.