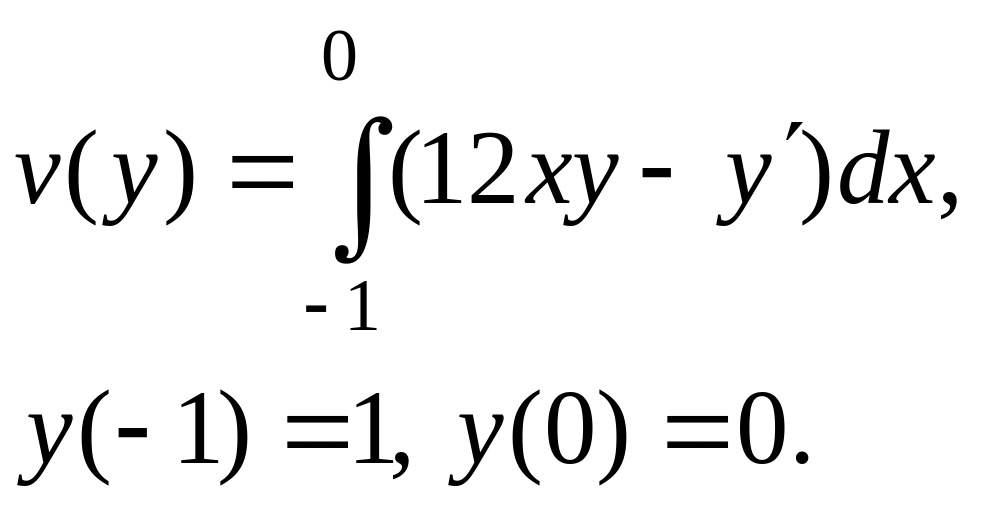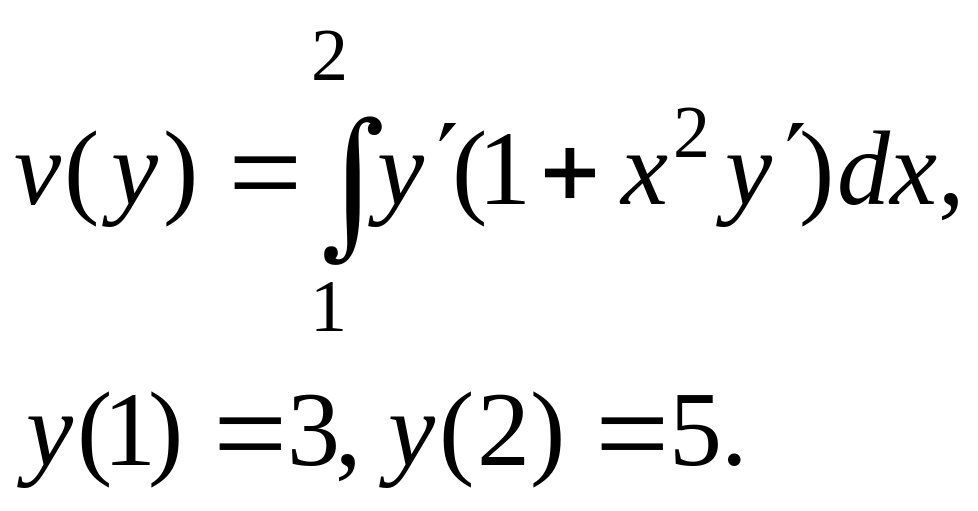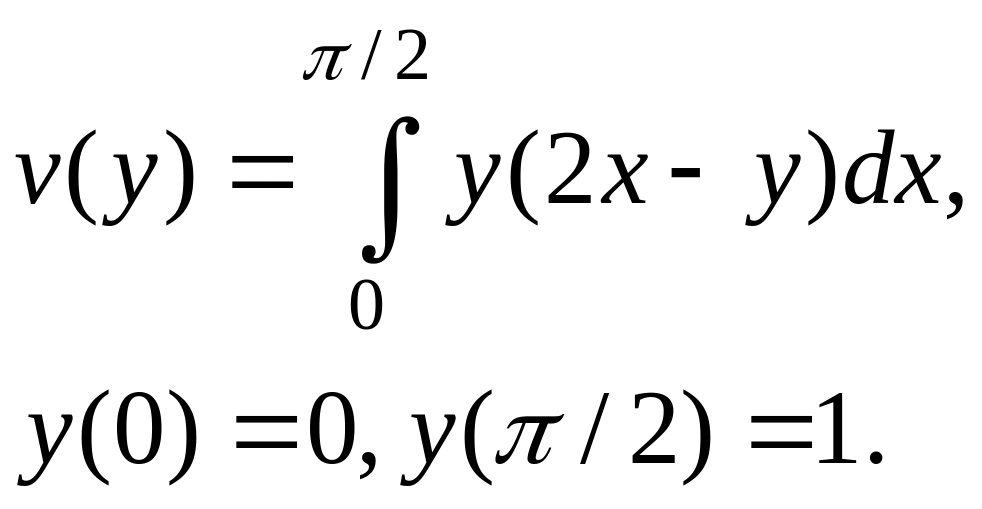- •Модуль іі. Диференціальні рівняння математичної фізики Розділ і. Диференціальні рівняння математичної фізики в частинних похідних § 22. Диференціальні рівняння в частинних похідних другого порядку
- •§23. Класифікація диференціальних рівнянь в частинних похідних
- •§ 24. Поперечні коливання струни. Рівняння гіперболічного типу
- •§25. Початкові та крайові умови.
- •§26. Задача Коші. Метод Даламбера розв’язування задачі Коші (метод біжучих хвиль)
- •§27. Метод відокремлення змінних. Метод Фур’є
- •§ 28. Рівняння параболічного типу.
- •2) Рівняння теплопровідності:
- •§ 29. Інтеграл Фур’є
- •§ 30. Поширення теплоти в безмежному стержні
- •§31. Рівняння еліптичного типу
- •§32. Формули Гріна
- •§33. Формули Гріна для гармонічних функцій
- •§34. Інтегральні формули ля гармонічних функцій
- •§ 35. Сферичні та кульові функції. Поліноми Лежандра.
- •Приклади розв’язання задач
- •Тема 9. Класифікація диференціальних рівнянь з частинними похідними другого порядку
- •Індивідуальні домашні завдання до теми 9
- •Тема 10. Зведення до канонічного вигляду диференціальних рівнянь з частинними похідними зі сталими коефіцієнтами
- •Індивідуальні домашні завдання до теми 10
- •Тема 11. Задача Коші для рівнянь гіперболічного типу. Метод характеристик
- •Індивідуальні домашні завдання до теми 11
- •Тема 12. Метод розділення змінних (метод Фур’є) для рівнянь гіперболічного типу
- •Індивідуальні домашні завдання до теми 12 розділ іі. Варіаційне числення § 36. Функціонали. Задачі варіаційного числення
- •§ 37. Варіація і її властивості.
- •§38. Рівняння Ейлера-Лагранжа
- •§39. Умовні екстремуми
- •Приклади розв’язання задач
- •Тема 13. Варіаційне числення
- •Отже, екстремум може досягатися лише на кривій .
- •Індивідуальні домашні завдання до теми 13
- •Додаток 1. Основні поняття векторної алгебри.
Приклади розв’язання задач
Тема 13. Варіаційне числення
Задача 1. На яких кривих може досягати екстремуму функціонал

Розв’язання.
Тут
![]() так що рівняння Ейлера має вигляд
так що рівняння Ейлера має вигляд
![]() .
Його загальний розв’язок:
.
Його загальний розв’язок:
![]()
Граничні
умови дають систему лінійних рівнянь
для визначення
![]() і
і
![]() :
:
 звідси
звідси ![]()
Отже, екстремум може досягатися лише на кривій .
Задача
2.
Знайти екстремалі функціонала
 що задовольняють граничні умови
що задовольняють граничні умови
![]()
Розв’язання.
Рівняння Ейлера має вигляд
![]() ,
звідки
,
звідки
![]() .
Так як екстремаль
не задовольняє умову
.
Так як екстремаль
не задовольняє умову
![]() ,
то дана варіаційна задача не має
розв’язку.
,
то дана варіаційна задача не має
розв’язку.
Задача 3. Знайти екстремалі функціоналу:

що
задовольняють граничні умови
![]() ,
,
![]() .
.
Розв’язання.
Рівняння Ейлера має вигляд
![]() ;
його характеристичне рівняння
;
його характеристичне рівняння
![]() має корені
має корені
![]() ,
а загальний розв’язок
,
а загальний розв’язок
![]() Використовуючи граничні умови, отримаємо:
Використовуючи граничні умови, отримаємо:
![]() ,
де
– довільна стала.
,
де
– довільна стала.
Індивідуальні домашні завдання до теми 13
1-26. Знайти екстремалі наступних функціоналів:
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
Додаток 1. Основні поняття векторної алгебри.
Ц ей
додаток включений для повторення
основних визначень векторної алгебри.
Вектор – напрямлений відрізок в просторі.
Позначається:
ей
додаток включений для повторення
основних визначень векторної алгебри.
Вектор – напрямлений відрізок в просторі.
Позначається:
![]() ,
де
,
де
![]() -
початкова точка,
-
початкова точка,
![]() -
кінцева точка; або
-
кінцева точка; або
![]() ,
,![]() …
Довжина вектора
називається
його модулем і позначається
…
Довжина вектора
називається
його модулем і позначається
![]() або
.
Одиничні вектори – вектори, довжина
яких дорівнюють 1. Два вектори називаються
рівними,
якщо рівні їх модулі і співпадають їх
напрямки (мал. 1)
або
.
Одиничні вектори – вектори, довжина
яких дорівнюють 1. Два вектори називаються
рівними,
якщо рівні їх модулі і співпадають їх
напрямки (мал. 1)
Множення
на скаляр:
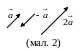 Якщо
-
дійсне число і
- вектор, то добуток
Якщо
-
дійсне число і
- вектор, то добуток
![]() також є вектор з довжиною
також є вектор з довжиною
![]() і напрямком, який співпадає з напрямком
вектора
,
якщо
і напрямком, який співпадає з напрямком
вектора
,
якщо
![]() ,
і з напрямком, протилежним напрямку
вектора
,
якщо
,
і з напрямком, протилежним напрямку
вектора
,
якщо
![]() (мал. 2)
(мал. 2)
Д
 одавання
векторів:
Сума
одавання
векторів:
Сума
![]() є вектор, який має початок, що співпадає
з початком
,
і кінець, який співпадає з кінцем
.
(правило трикутника, мал. 3). Взагалі сума
є вектор, який має початок, що співпадає
з початком
,
і кінець, який співпадає з кінцем
.
(правило трикутника, мал. 3). Взагалі сума
![]() кількох векторів
,
,…,
кількох векторів
,
,…,![]() визначається як вектор
визначається як вектор
![]() ,
який замикає колону складену із
,
,…,
(мал.
4).
,
який замикає колону складену із
,
,…,
(мал.
4).
 Віднімання
векторів:
Різниця векторів
Віднімання
векторів:
Різниця векторів
![]() розглядається як сума
і
розглядається як сума
і
![]() (мал.
5).
(мал.
5).
Два
вектора
і
називаються
колінеарними, якщо прямі, що проходять
в напрямках
і
,
паралельні. Три вектори
,
,
![]() називаються компланарними, якщо вони
паралельні одній площині. Якщо
і
не
колінеарні, або
,
,
не компланарні, то їх називають лінійно
незалежними на площині або в просторі
(тобто
називаються компланарними, якщо вони
паралельні одній площині. Якщо
і
не
колінеарні, або
,
,
не компланарні, то їх називають лінійно
незалежними на площині або в просторі
(тобто
![]() або
або
![]() тільки при
тільки при
![]() ).
Два вектори
і
ортогональні (
).
Два вектори
і
ортогональні (
![]() ),
якщо вони взаємно перпендикулярні.
),
якщо вони взаємно перпендикулярні.
Д
![]() ля
представлення векторів часто
використовується Декартова система
координат, яка утворюється трьома
напрямленими прямим
ля
представлення векторів часто
використовується Декартова система
координат, яка утворюється трьома
напрямленими прямим
![]() -
вісями координат, що не лежать в одній
площині. В прямокутній системі координат
вісі взаємно ортогональні. Найбільше
зустрічається права система координат
(мал. 6), в якій вісі
мають таку ж орієнтацію, як великий,
вказівний і середній пальці правої
руки. Інакше матимемо ліву систему
координат.
-
вісями координат, що не лежать в одній
площині. В прямокутній системі координат
вісі взаємно ортогональні. Найбільше
зустрічається права система координат
(мал. 6), в якій вісі
мають таку ж орієнтацію, як великий,
вказівний і середній пальці правої
руки. Інакше матимемо ліву систему
координат.
Кожна
точка
![]() в просторі може бути задана своїм радіус
вектором
в просторі може бути задана своїм радіус
вектором
![]() :
:
![]() ,
де
,
де
![]() - одиничні вектори, напрямок яких
співпадає з напрямками вісей
відносно
і називаються базисними векторами.
Величини
- одиничні вектори, напрямок яких
співпадає з напрямками вісей
відносно
і називаються базисними векторами.
Величини
![]() називаються декартовими координатами;
при цьому пишуть
називаються декартовими координатами;
при цьому пишуть
![]() або
або
![]() .
.
 В
прямокутній декартовій системі координат
будь-який вектор
можна представити в вигляді:
В
прямокутній декартовій системі координат
будь-який вектор
можна представити в вигляді:
![]() ;
де
;
де
![]() називаються декартовими координатами
вектора
(мал. 7)
називаються декартовими координатами
вектора
(мал. 7)
Добуток
векторів: Скалярний
добуток
векторів
і
,
який позначають
![]() є число
є число
![]() ,
де
,
де
![]() - кут між векторами
і
.
- кут між векторами
і
.
 Під
векторним
добутком
векторів
і
,
який позначають
Під
векторним
добутком
векторів
і
,
який позначають![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
розуміють вектор
,
який має довжину
,
розуміють вектор
,
який має довжину
![]() (площа паралелограма, побудованого на
і
як на сторонах) і спрямований
до
і
,
причому так, що вектори
(площа паралелограма, побудованого на
і
як на сторонах) і спрямований
до
і
,
причому так, що вектори
![]() утворюють праву трійку векторів.
Подвійний векторний добуток:
утворюють праву трійку векторів.
Подвійний векторний добуток:
![]() -
це вектор компланарний векторам
і
і обчислюється по формулі:
-
це вектор компланарний векторам
і
і обчислюється по формулі:
![]() .
.
З мішаний
добуток
мішаний
добуток
![]() є скаляр, абсолютна величина якого
дорівнює об’єму паралелепіпеда,
побудованого на векторах
,
,
.
Змішаний добуток додатній, якщо
,
,
утворюють праву трійку, і відємний в
протилежному випадку. Замість
пишуть також
є скаляр, абсолютна величина якого
дорівнює об’єму паралелепіпеда,
побудованого на векторах
,
,
.
Змішаний добуток додатній, якщо
,
,
утворюють праву трійку, і відємний в
протилежному випадку. Замість
пишуть також
![]() або
або
![]() .
Перестановка двох співмножників змінює
знак у змішаному добутку:
.
Перестановка двох співмножників змінює
знак у змішаному добутку:
![]()
Якщо , , задані в прямокутній декартовій системі координат:
![]() ,
,
![]() ,
,
![]() то добутки можна виразити через декартові
координати векторів:
то добутки можна виразити через декартові
координати векторів:
скалярний
добуток:
![]() ;
;
векторний добуток:
 ;
;
змішаний
добуток:
 .
.
1Кажуть, що функція f(x) задовольняє в інтервалі (а, b) умови Діріхле, якщо вона або неперервна в цьому інтервалі, або має скінченну кількість розривів першого роду і, крім того, має скінченну кількість максимумів та мінімумів в цьому інтервалі.