§38. Рівняння Ейлера-Лагранжа

Дослідимо на екстремум функціонал

, (1)

причому граничні точки допустимих кривих закріплені: (див. мал.) Функцію будемо вважати тричі диференційованою.

М и вже знаємо, що необхідною умовою екстремуму є обертання в 0 варіації функціоналу. Припустимо, що екстремум досягається на двічі диференційованій кривій . Візьмемо деяку близьку до допустиму криву і включимо криві і в однопараметричне сімейство кривих

(2)

при отримаємо криву , на якій досягається екстремум; при маємо . Різниця називається варіацією функції .

Якщо розглядати значення функціонала (1) тільки на кривих сімейства , то функціонал перетворюється у функцію :

.

Ця функція досягає свого екстремуму при , тому що при отримуємо , на якій функціонал досягає свого екстремуму порівняно з любими близькими допустимими кривими, в т.ч. з близькими кривими . Необхідною умовного екстремуму функції при є . Але оскільки , то , де , , або, оскільки

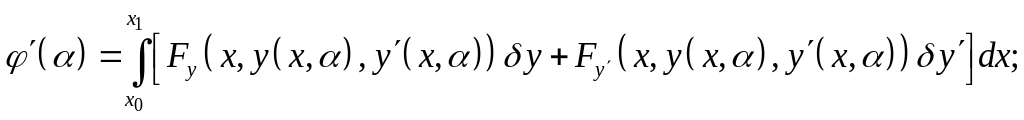
Як ми вже знаємо, є варіацією функціонала. Необхідною умовою екстремуму є обернення в 0 його варіації: . Для функціонала (1) ця умова має вигляд:

Інтегруючи 2-й додаток по частинам і приймаючи до уваги, що отримаємо

Але і , тому що всі допустимі криві в розглянутій задачі проходять через фіксовані граничні точки. Отже,

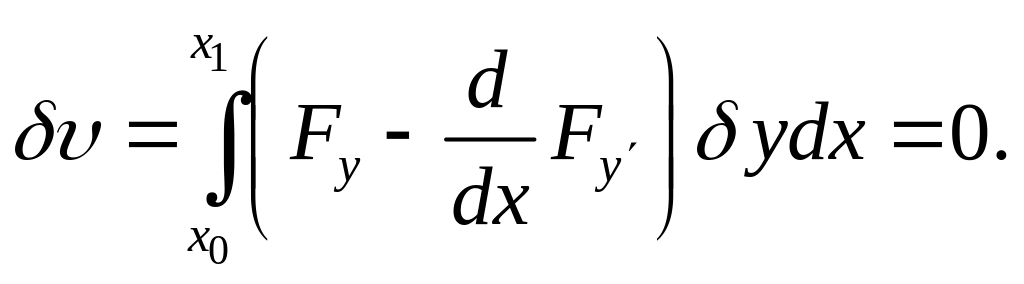. (3)

причому 1-й множник на кривій , яка реалізує екстремум, є заданою неперервною функцією, а другий множник внаслідок довільності у виборі кривої порівняння , є довільною функцією, що задовольняє лише досить загальним умовам, а саме: функція в граничних точках і обертається в 0, є диференційованою і , малі по абсолютній величині. За цієї причини інтеграл в (2) дорівнюватиме 0 тільки при умові, що вираз в дужках : на кривій , яка реалізує екстремум досліджуваного функціонала, тобто є розв’язком диференційного рівняння 2-го порядку: , або в розгорнутому вигляді

. (4)

Це рівняння називається рівнянням Ейлера-Лагранжа. Його інтегральні криві називаються екстремалями. Тільки на екстремалях може досягатись екстремум функціонала (1). Для знаходження кривої, що реалізує екстремум функціонала (1), інтегрують рівняння Ейлера-Лагранжа і визначають обидві довільні сталі , що входять в загальний розв’язок цього рівняння, із умов на границі . Тільки на задовольняючих цим умовам екстремалях може реалізуватись екстремум функціонала.

Якщо ми шукаємо екстремум функціонала більш загального виду

(5)

при заданих граничних значеннях всіх функцій

, (6)

то варіюючи лише одну з функцій і залишаючи всі інші функції незмінними, прийдемо до рівняння Ейлера

Оскільки ці міркування можна застосувати до будь-якої функції то отримаємо систему диференціальних рівнянь 2-го порядку

(7)

які визначають сімейство екстремалей даної варіаційної задачі.

§39. Умовні екстремуми

Варіаційними задачами на умовний екстремум називаються задачі, в яких вимагається найти екстремум функціонала , причому на функції, від яких залежить функціонал , накладаються деякі додаткові умови – так звані в’язі. Наприклад, потрібно знайти екстремум функціонала

(1)

при наявності додаткових умов у вигляді

а) рівнянь в’язів, які не містять похідних від функцій:

(2)

б) або у вигляді диференційних рівнянь:

. (3)

В механіці в’язі типу (2) називаються голономними, а в’язі типу (3) – неголономними.

У варіаційному численні доказується, що умовний екстремум функціонала (1)досягається на тих же кривих, на яких реалізується безумовний екстремум функцією

, (4)

де невідомі функції називаються множниками Лагранжа, а

.

(Якщо умови мають вигляд: , тоді

, ). (5)

Якщо задача має розв’язок, то функцій визначаються із рівнянь, що складаються з рівнянь в’язів (2) або (3) і системи диференціальних рівнянь Ейлера-Лагранжа:

. (6)

Для прикладу приведемо знамениту задачу Дідо. У давнину фінікійська цариця Дідо, тікаючи від властителя сусідньої держави, добралась до Північної Африки і звернулась до місцевого племені з проханням приютити її, виділивши для цього стільки землі, скільки можна охопити шкурою вола. Коли плем’я погодилося, Дідо розрізала шкуру на тонкі шнурки і, зв’язавши їх в довгу нитку, охопила нею чималу по тим часам ділянку землі, на якій згодом розгорнула будівництво і заснувала знамените місто Карфаген. Задача полягає в тому: як Дідо мала розташувати свою нитку, щоб охопити найбільшу площу, тобто як вибрати із всіх ліній заданої довжини ту, що охоплює найбільшу площу . Виявилось, що розв’язком цієї задачі є коло (якщо лінія береться замкнутою), або дуга кола (якщо лінія береться незамкнутою), наприклад, якщо Дідо розташувала свою нитку кінцями біля моря.