Індивідуальні домашні завдання до теми 2

1-2. Визначити циркуляцію вектора , де - стала:

1. вздовж кривої ,

2. вздовж кривої .

3. Обчислити циркуляцію векторного поля вздовж криої .

4-6. Користуючись формулою Гауса-Остроградського, перетворити поверхневі інтеграли в інтеграли по об’єму:

4.

5.

6.

7-9. За допомогою формули Гауса-Остроградського визначити наступні інтеграли:

7. , де поверхня еліпсоїда ;

8. , де поверхня сфери ;

9. , де поверхня конуса .

10. Користуючись формулою Гауса-Остроградського, перетворити поверхневий інтеграл в інтеграл по об’єму.

11-17. Знайти дивергенцію поля:

11. ;

12. ;

13. ; 14. ;

15. ; 16. ;

17. .

18-22. Обчислити

18. ; 19. ; 20. ;

21. ; 22. ,

де сталий вектор.

Тема 3: Теорема Стокса. Ротор векторного поля

Задача 1. Визначити циркуляцію вектора вздовж кола в додатному напрямку.

Розв’язання.

Відповідно:

За формулою Стокса: .

Задача 2-4. Застосовуючи формулу Стокса, визначити інтеграли:

2. , де - крива , обхід здійснювати проти годинникової стрілки, якщо дивитись з позитивного напрямку вісі .

Розв’язання. Застосуємо формулу Стокса, взявши в якості поверхні - коло радіусом , яке лежить в площині , отримаємо:

де напрямні косинуси нормалі до поверхні - площини так як нормаль в цій площині утворює з додатнім напрямком осі гострий кут, то в кожній із формул для визначення перед знаком радикала візьмемо знак .

Зрозуміло, що тоді:

.

3. де замкнута крива , обхід здійснювати в напрямку зростання параметра

Розв’язання. При зміні від до точка проходить криву від точки до точки а при зміні від до точка проходить ту ж саму частину кривої в протилежному напрямку - від точки , до точки . Таким чином , точки замкнутої кривої взаємно накладаються і крива не обходить ніяку поверхню, тому

Задача 4. Знайти ротор векторного поля

Розв’язання.

тоді .

Задача 5. Знайти якщо .

Розв’язання. , тоді

.

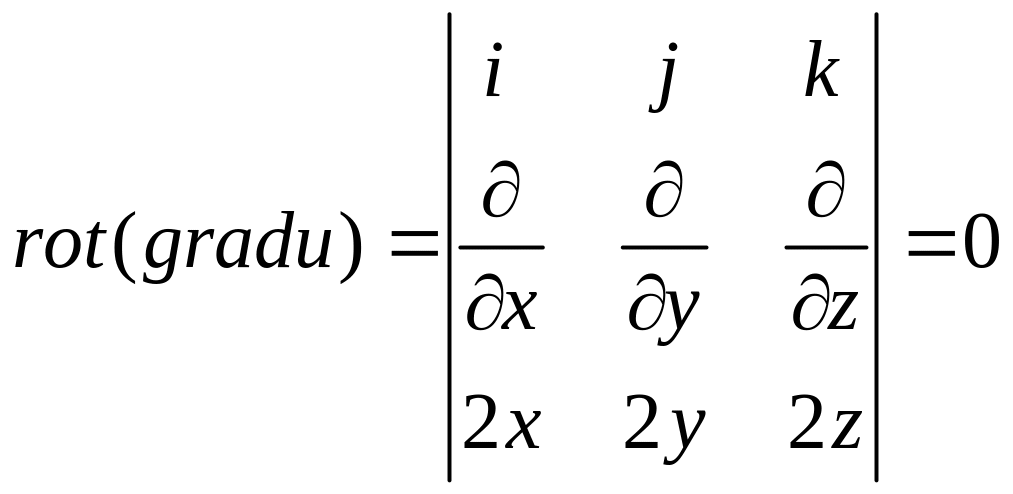Задача 6. Знайти ротор лінійної швидкості твердого тіла, яке обертається навколо нерухомої точки з кутовою швидкістю

Розв’язання. Як відомо, швидкість твердого тіла визначається за формулою:

.

Звідси знаходимо:

Таким чином, дорівнює подвійній швидкості обертання.

Задача 7. Довести, що вихровий характер поля досягає найбільшого значення в напрямку ротора.

Розв’язання. Завихреність поля в напрямку рівна проекції ротора на цей напрямок, тобто: Звідси видно, що поле має найбільшу завихреність у випадку, коли а це означає, що напрямок нормалі співпадає з напрямком при чому найбільша завихреність рівна .

Задача 8. Визначити ротор векторного поля:

Розв’язання.

.

Індивідуальні домашні завдання до теми 3

1. За допомогою формули Стокса перетворити інтеграл , взятий по деякому замкнутому контурі, в інтеграл по поверхні.

2. Використовуючи формулу Стокса визначити інтеграл , де контур коло , взявши в якості поверхні півсферу . Інтегрування по колу в площині здійснюється в додатньому напрямку.

3-5. Довести властивості ротора:

3. , де ;

4. , де сталі коефіцієнти.

5. , де скалярне поле.

6. Визначити ротор векторного поля в точці .

7 . Знайти функцію векторного поля вздовж замкнутої лінії , де дуга астроїди, яка визначається рівнянням: або

Вказівка. Слід застосувати формулу Стокса.

8. За допомогою формули Стокса знайти циркуляцію векторного поля: вздовж контура квадрата , який визначається рівняннями:

9-10. Визначити за допомогою формули Стокса циркуляцію векторного поля вздовж поверхонь:

9. (вектор додатної нормалі );

10. (вектор додатної нормалі ).

11. Довести, що

12. Знайти величину і напрямок в точці , якщо .

13-17. Знайти ротор векторних полів

13. ; 14. ; 15. ;

16. ; 17. ,

де сталі вектори.