§5. Дивергенція векторного поля
Векторне поле – це частина простору (або весь простір), кожній точці якого у відповідності з певним законом заданий деякий вектор.
З точки
зору математики задання векторного
поля еквівалентно заданню векторної
функції
,
яку будемо вважати однозначною,
неперервною, диференційованою.
П
риклади
векторних полів: напруженість
електростатичного поля; індукція
магнітного
поля; поле градієнта довільного скаляра.
Векторною
лінією поля
називають криву, в кожній точці якої
дотична має напрямок вектора поля.
Диференційне
рівняння векторних ліній випливає із
умови паралельності нескінченно малого
елемента векторної лінії
(з проекціями
)
і вектора поля
(з проекціями
):
,
звідки
(1)
Розглянемо
поле
з відповідними компонентами вздовж
вісей координат
,
,
.
Дивергенцією вектора
(запис
)
називають суму частинних похідних типу
.
(2)
Дивергенція однозначно визначається в кожній точці векторного поля і задає певне скалярне поле ( - скаляр). Дивергенцію вектора можна розглядати як формальний скалярний добуток «вектора» на вектор поля :
.
Отже,
(3)
Приклад:
знайдемо
:
;
.
Властивості дивергенції:
Лінійність:
(
)
.
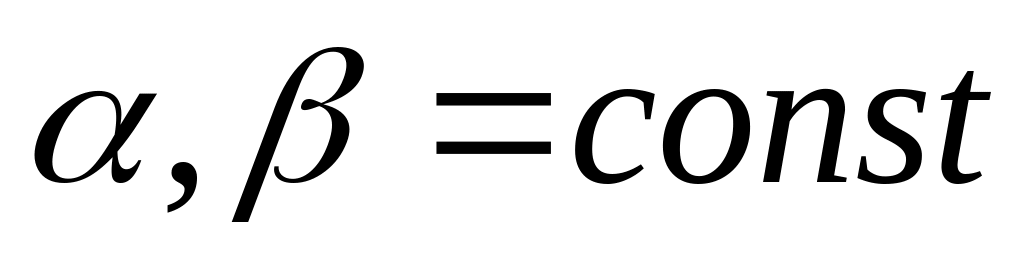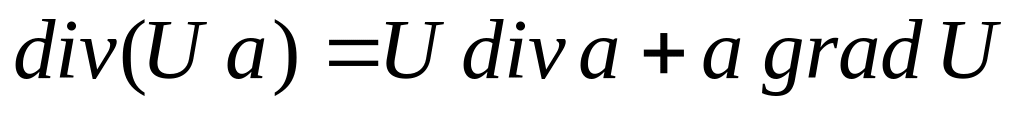Це можна перевірити, скориставшись
безпосереднім визначенням (2):
§6. Поверхневий інтеграл і потік векторного поля
В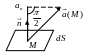
заданому векторному полі
візьмемо нескінчено малу площадку
з одиничним вектором нормалі
в точці
.
Розглянемо в точці
вектор поля
і позначимо через
його проекцію на нормаль (див. мал.).
Величину, яка дорівнює добутку
на
:
(1)
називають елементарним потоком векторного поля . Елементарний потік залежить від вибору площадки і напрямку нормалі (їх може бути 2).
Введемо
тепер поняття поверхневого інтеграла.
Нехай в точках деякої двохсторонньої
поверхні визначена функція
.
Розіб’ємо поверхню на велику кількість
малих ділянок
,
на кожній з яких візьмемо довільну очку
і
обчислимо суму для всієї поверхні:
.
Границя (межа) цієї суми (якщо вона існує)
при наближенні всіх
до нуля називається поверхневим
інтегралом від функції
по поверхні
і позначається символом
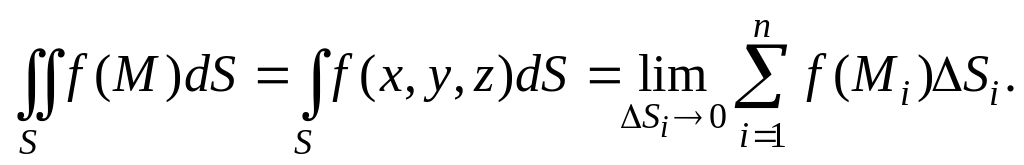
На основі поняття поверхневого інтегралу вводиться поняття потоку вектора через поверхню. Векторне поле визначає в точках поверхні деяку скалярну функцію ( - проекція вектора на напрямок нормалі в точках поверхні ). Поверхневий інтеграл
(2)
називають
потоком вектора
через поверхню
в заданому напрямку нормалі. Отже, потік
вектора означає поверхневий інтеграл
від нормальної складової вектора поля.
Приклад 1:
-
густина струму,
-
сила струму. Приклад 2: Всередині
нерівномірно нагрітого твердого тіла
виділимо деяку поверхню
.
Через ділянку
цієї поверхні за одиницю часу проходить
кількість тепла
,
де
- густина теплового потоку. Через всю
поверхню
за одиницю часу проходить енергія
.
Цей інтеграл є потоком вектора
через поверхню
.
§7. Теорема Остроградського – Гауса
В
становимо
зв'язок між дивергенцією і потоком.
Побудуємо в заданому векторному полі
невеликий паралелепіпед з центром в
довільній точці
,
грані якого нехай будуть паралельними
координатним площинам, а ребра дорівнюють
.
Позначимо
через
центри тих граней, які
до
вісі
;
координати цих точок такі:
і
.
Потік
вектора
через грань паралелепіпеда з центром
в напрямку зовнішньої до паралелепіпеда
нормалі дорівнює
,
(1)
а
через грань з центром
,
(2)
(Тут
враховано, що напрямок зовнішньої
нормалі в точці
протилежний до напрямку вісі
).
Сума потоків (1) і (2) через дві протилежні
грані паралелепіпеда дорівнює
. (3)
Але
(4)
[де
враховано, що при
].
Тоді
(3) приймає вигляд
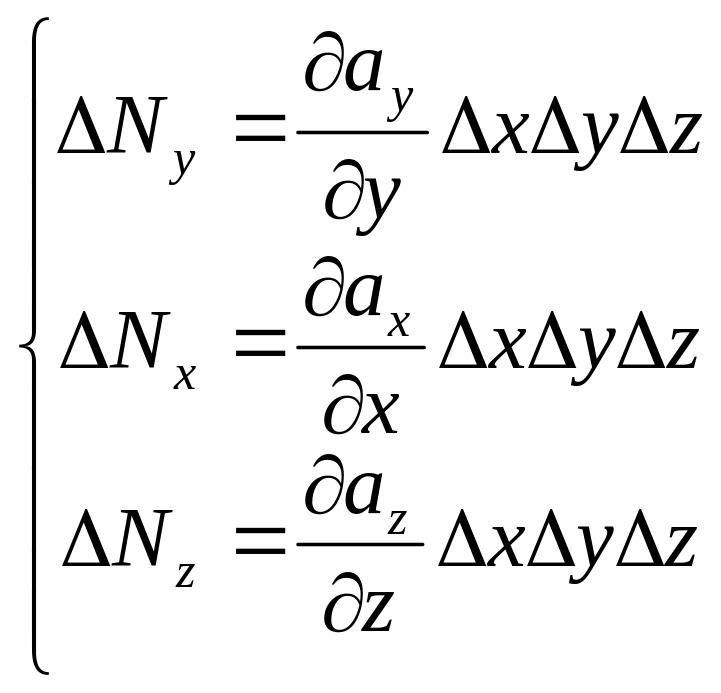
Повний потік вектора через поверхню паралелепіпеда
.
(5)
В
ізьмемо
довільний об’єм
,
обмежений замкнутою поверхнею
.
Розіб’ємо його на сукупність елементарних
паралелепіпедів трьома сімействами
площин, паралельних координатам, і
складемо рівності типу (5) для всіх
елементарних паралелепіпедів об’єму
.
При підсумовуванні врахуємо, що внутрішні
поверхні не будуть входити в поверхневий
інтеграл, тому що вони входять двічі,
але з протилежними знаками:
Тому
отримаємо:
,
тобто
(6)
Ця рівність виражає теорему Остроградського – Гауса: Потік вектора через замкнуту поверхню дорівнює об’ємному інтегралу від дивергенції векторного поля по об’єму, який обмежений даною поверхнею.