1.8. Метод Ньютона.

Пусть f(x) – дважды непрерывно дифференцируемая функция, причем f ''(x) > 0. Тогда, как уже указывалось в предыдущем разделе, решение задачи минимизации функции f (x) сводится к решению нелинейного уравнения f ^'(x) = 0.

Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений.

Пусть корень x^*  [a, b], так, что f '(a)f '(b) < 0. Положим x₀ = b. Проведем касательную к графику функции y = f '(x) в точке B₀ = (x₀, f '(x₀)) (рис. 1.5).

Рис. 1.5

Уравнение касательной будет иметь вид:

y – f '(x₀) = f"(x₀)(x – x₀). (1.16)

Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (1.16) y = 0, x = x₁:

x₁ = x₀ – . (1.17)

Аналогично поступим с точкой B₁(x₁, f '(x₁)), затем с точкой B₂(x₂, f '(x₂)), и т. д. в результате получим последовательность приближений x₁, x₂, …, x_n , …, причем

x_{n +1} = x_n – 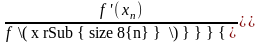. (1.18)

Формула (1.18) является расчетной формулой метода Ньютона.

При заданной точности  > 0 вычисления по формуле (1.18) нужно вести до тех пор, пока не будет выполнено неравенство| f '(x_n)|  , после чего полагают x^*  x_n.

Алгоритм 1.6 (Алгоритм метода Ньютона).

Шаг 1. Ввести исходные данные: a, b, . Положить n = 0, x₀ = b.

Шаг 2. Вычислить f ^'(x_n) и f ^"(x_n).

Шаг 3. Вычислить x_{n +1} = x_n – .

Шаг 4. Проверить критерий окончания вычислений. Если f ^'(x _{n +1})  , , перейти к шагу 6, иначе – к шагу 5.

Шаг 5. Положить n = n +1. Перейти к шагу 2.

Шаг 6. Положить x^*  x_{n +1} . Вычислить f^'(x^*).

Пример 1.7.

Методом Ньютона найдем точку минимума функции f(x) = xarctgx – ln(1 + x² ) на отрезке [0, 1],  = 10 ^–7.

Функция f(x) дважды дифференцируема, причем

f ^'(x) = arctgx, f ^"(x) = 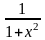> 0.

Расчетные формулы (1.18) примут вид:

x_{n +1} = x_n – arctgx(1 + x²).

Результаты вычислений приведены в табл. 1.8.

Таблица 1.8

n	xn	f '(xn)
0 1 2 3 4	1 -0.570 0.117 -0.06110-3 910-8	0.785 -0.519 0.116 -1.06110-3 910-8

Вычисления прекращаются, так как требуемая точность достигнута (910^-8 < 10 ^–7).

Таким образом, x^*  910^-8  0, f(x^*)  0.

Тема 2. Задачи многомерной безусловной минимизации

2.1. Необходимые сведения из курса линейной алгебры

Пусть f(x₁, x₂, … ,x_n) – действительная функция n переменных, определенная на множестве X  Rⁿ (Rⁿ – n-мерное пространство, в частности, R² – плоскость). Обозначим через x вектор-столбец

= (x₁, x₂, …, x_n)^T, (2.1)

где символ "T" – знак транспонирования. Тогда x –точка в пространстве Rⁿ и f(x) =f(x₁, x₂, … ,x_n).

Скалярное произведение векторов x = (x₁, x₂, …, x_n)^T и y = (y₁, y₂, …, y_n)^T определяется следующим образом:

(x, y) = 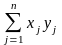. (2.2)

Нормой (длиной) вектора x называется число

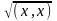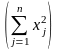
x = = . (2.3)

Определено расстояние между векторами x и y:

(x, y) = x – y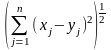 = . (2.4)

Матрица A =(a_ij), i = 1, … , m; j = 1, … , n, представляет собой прямоугольную таблицу размера mn, состоящую из m строк и n столбцов. В частности, вектор-столбец x является матрицей размера n 1.

Квадратная матрица A называется симметрической, если a_ij = a_ji, i, j = 1, … , n.

Произведением матрицы A размера mn на вектор-столбец x  Rⁿ является вектор-столбец b = (b₁, b₂, … , b_m)^T R^m, координаты которого вычисляются по формуле:

b_i = 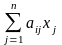= (aⁱ, x) , i = 1, 2, …, m, (2.5)

где aⁱ = (a_i1, … , a_in) – i-ая строка матрицы A, т. е. Ax = b.

Определителем квадратной матрицы A (обозначается detA или A) размера nn называется число, которое определяется по формуле:

detA = A = . (2.6)

Здесь A_ij – алгебраическое дополнение элемента a_ij, A_ij = (–1)^i+jM_ij , а M_ij – минор, который является определителем матрицы, полученной из A вычеркиванием i-ой строки и j-го столбца.

Если определитель матрицы A не равен нулю, то существует обратная матрица A^–1 = (_ij). Элементы обратной матрицы находят по формуле:

_ij = 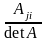, (2.7)

где A_ji – алгебраическое дополнение элемента a_ji матрицы A.

Квадратичной формой Q от n переменных x₁, x₂, …, x_n называется сумма, каждый член которой является либо квадратом одного из этих переменных, либо произведением двух разных переменных. Считая, что в квадратичной форме Q уже сделано приведение подобных членов, введем следующие обозначения: коэффициент при x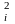 обозначим через a_ii, а коэффициент при произведении x_ix_j для i  j – через 2a_ij. Член 2a_ijx_ix_j можно записать в виде

2a_ijx_ix_j = a_ijx_ix_j + a_jix_jx_i.

Очевидно, что a_ij = a_ji. Всю квадратичную форму Q можно записать в виде суммы всевозможных членов a_ijx_ix_j, где i и j независимо друг от друга принимают значения от 1 до n:

Q = . (2.8)

В частности, при i = j получается член a_iix .

Из коэффициентов a_ij можно составить квадратную матрицу A = (a_ij) размера nn; она называется матрицей квадратичной формы Q.

Так как a_ij = a_ji, матрица A является симметрической.

Квадратичную форму Q можно записать в ином виде, используя введенное ранее умножение матрицы на вектор-столбец и скалярное произведение векторов. Равенство (2.8) равносильно равенству

Q(x) = = (Ax, x). (2.9)

Квадратичная форма Q(x) называется положительно определенной, если для всех x  0 имеет место неравенство Q(x) > 0.

Из курса линейной алгебры известен критерий Сильвестра положительной определенности квадратичной формы: для того, чтобы квадратичная форма Q(x) была положительно определенной, необходимо и достаточно, чтобы ее матрица A = (a_ij) была положительно определена, т. е. все ее угловые миноры были положительными:

a₁₁ . . . a₁₂

a₁₁ a₁₂ . . _.

₁ = a₁₁ > 0; ₂ = > 0; _n = . . > 0. (2.10)

a₂₁ a₂₂ . .

a₁₁ . . . a₁₂