Расчетное задание №1

Таблица 1.1. Список задач по вариантам для расчетного задания № 1.

Вар 1	Вар 2	Вар 3	Вар 4	Вар 5
1.1.1 1.2.1 1.3.1	1.1.2 1.2.2 1.3.2	1.1.3 1.2.3 1.3.3	1.1.4 1.2.4 1.3.4	1.1.5 1.2.5 1.3.5
Вар 6	Вар 7	Вар 8	Вар 9	Вар 10
1.1.6 1.2.6 1.3.6	1.1.7 1.2.7 1.3.7	1.1.8 1.2.8 1.3.8	1.1.9 1.2.9 1.3.9	1.1.10 1.2.10 1.3.10
Вар 11	Вар 12	Вар 13	Вар 14	Вар 15
1.1.11 1.2.11 1.3.11	1.1.12 1.2.12 1.3.12	1.1.13 1.2.13 1.3.13	1.1.14 1.2.14 1.3.14	1.1.15 1.2.15 1.3.15
Вар 16	Вар 17	Вар 18	Вар 19	Вар 20
1.1.16 1.2.16 1.3.16	1.1.17 1.2.17 1.3.17	1.1.18 1.2.18 1.3.18	1.1.19 1.2.19 1.3.19	1.1.20 1.2.20 1.3.20
Вар 21	Вар 22	Вар 23	Вар 24	Вар 25
1.1.21 1.2.21 1.3.21	1.1.22 1.2.22 1.3.22	1.1.23 1.2.23 1.3.23	1.1.24 1.2.24 1.3.24	1.1.25 1.2.25 1.3.25
Вар 26	Вар 27	Вар 28	Вар 29	Вар 30
1.1.26 1.2.26 1.3.26	1.1.27 1.2.27 1.3.27	1.1.28 1.2.28 1.3.28	1.1.29 1.2.29 1.3.29	1.1.30 1.2.30 1.3.30

Задача 1. Взаимодействие системы точечных зарядов.

1. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см³. Какой должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина

2. В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда так как указано на рисунке 1. Найдите напряженность электрического поля в центре шестиугольника, если каждый заряд q=1,5 нКл., сторона шестиугольника 3 см.

3. Р ешить предыдущую задачу для расположения зарядов указан­ного на рисунке 2

4. Решить задачу 1.2 при условии что все шесть зарядов, расположенных в вершинах шестиугольника положительны.

5. Два маленьких заряженных шарика, одинаковых по размеру, притягиваются друг к другу с некоторой силой. После того как шарики были приведены в соприкосновение и раздвинуты на расстояние в два раза большее, чем прежде, сила взаимодействия между ними уменьшилась в три раза. Какова была величина первого заряда Q₁ , если второй имел заряд Q₂=10 нКл?

6. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда мкКл они оттолкнулись друг от друга и разошлись на угол . Найдите массу m каждого шарика, если расстояние от центра шарика до точки подвеса l=20 см.

7. В вершинах правильного шестиугольника со стороной а=10 см расположены точечные заряды Q, 2Q, 3Q, 4Q, 5Q, 6Q (Q = 0,1 мкКл). Найдите силу F, действующую на точечный заряд Q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.

8. Два точечных заряда, находясь в воздухе на расстоянии r₁=10см друг от друга, взаимодействуют с некоторой силой. На каком расстоянии r₂ надо поместить эти заряды в масле, чтобы получить ту же силу взаимодействия?

9. Два точечных заряда нКл и нКл расположены на расстоянии r=5 см. Найдите напряженность E электрического поля точке, находящейся на расстояниях а=3 см. от положительного заряда и b=4 см. от отрицательного заряда.

10. Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 мм уравновешивается кулоновской силой отталкивания. Определите заряд капель. Плотность воды равна 1000

11. Расстояние d между точечными зарядами и равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность Е поля зарядов равна нулю.

12. Во сколько раз сила гравитационного притяжения между двумя протонами меньше силы их электростатического отталкивания?

13. В центр квадрата, в каждой вершине которого находится заряд нКл, помещен отрицательный заряд . Найдите этот заряд, если на каждый заряд действует результирующая сила F=0.

14. Найдите напряженность Е электрического поля в точке, лежащей посередине между точечными зарядами нКл и  нКл Расстояние между зарядами 10 см.

15. Два заряда 9Q и -Q закреплены на расстоянии l=50 см друг от друга. Третий заряд Q₁ может перемещаться только вдоль прямой, проходящей через заряды. Определите положение заряда Q₁, при котором он будет находиться в равновесии. При каком знаке заряда равновесие будет устойчивым?

16. В вершинах равностороннего треугольника находятся одинаковые положительные заряды Q=2 нКл. Какой отрицательный заряд Q₁ необходимо поместить в центр треугольника, чтобы сила притяжения с его стороны уравновесила силы отталкивания положительных зарядов?

17. Два одинаковых небольших шарика массой m=0,1 кг. Подвешены на нитях одинаковой длины L=20 см. После того как шарикам были сообщены одинаковые заряды, они разошлись на расстояние S=10 см. Определите заряды шариков.

18. Электрическое поле создано двумя точечными зарядами  нКл и  нКл, находящимися на расстоянии d=20 см друг от друга. Определите напряженность Е поля в точке, удаленной от первого заряда на расстояние 30 см и от второго на расстояние 50 см.

19. Найдите силу F притяжения между ядром атома водорода и электроном. Радиус атома водорода м. Заряд ядра равен по модулю и противоположен по знаку заряду электрона.

20. Расстояние d между зарядами  нКл. и  нКл. равно 10 см. Определите силу F, действующую на заряд нКл, расположенный на расстоянии 12 см от первого заряда и 10 см. от второго.

21. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так что их поверхности соприкасаются. Какой заряд Q надо сообщить шарикам, чтобы сила натяжения нитей стала равной Т=98 мН? Расстояние от центра шарика до точки подвеса l=10 см, масса шарика m=5 г.

22. В вершинах квадрата находятся одинаковые заряды Q=0,3 нКл. каждый. Какой отрицательный заряд Q₁ надо поместить в центр квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного?

23. Три точечных заряда нКл и нКл находятся в вершинах равностороннего треугольника со стороной а=10 см. Определите напряженность и потенциал электрического поля в центре треугольника.

24. Расстояние d между двумя точечными положительными зарядами равно 8 см. На каком расстоянии от первого заряда находится точка, в которой напряженность поля Е равна нулю?

25. В трех вершинах квадрата со стороной 40 см находятся одинаковые положительные заряды по Кл. Каждый. Найдите напряженность поля в четвертой вершине?

26. Расстояние l между свободными зарядами нКл и нКл равно 60 см. Определите точку на прямой проходящей через заряды, в которой нужно поместить третий заряд так, чтобы система зарядов находилась в равновесии. Определите величину и знак заряда. Будет ли равновесие устойчивым?

27. Даны два шарика массой m=1 г. Каждый. Какой заряд Q надо сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновешивала силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.

28. Два положительных точечных заряда Q и 4Q закреплены на расстоянии 60 см друг от друга. Определите, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд , чтобы он находился в равновесии. Указать какой знак должен иметь этот заряд чтобы равновесие было устойчивым. Перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.

29. Два одинаковых проводящих заряженных шара находятся на расстоянии r=30 см. Сила притяжения F₁ шаров равна 90 мкН. После того как шары были приведены в соприкосновение, а затем удалены друг от друга на прежнее расстояние, они стали отталкиваться с силой F₂ равной 160 мкН. Определите заряды Q₁ и Q₂, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.

30. Четыре маленьких шарика соединены тонкими непроводящими нитями так, что образуют ромб. Чему равен угол между нитями, если шарики, находящиеся в противоположных вершинах ромба имеют заряды и ?

Задача 2. Распределенные заряды

1. С какой силой электрической поле бесконечной плоскости действует на единицу длины заряженной нити, помещенной в это поле? Линейная плотность заряда на нити , поверхностная плотность заряда на плоскости

2. С какой силой на единицу длины отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда , находящиеся на расстоянии см друг от друга?

3. На рисунке 3 АС - заряженная бесконечная плоскость с поверхностной плотностью заряда и В – одноименно заряженный шарик массой m=1 г. И зарядом q=1 нКл. Какой угол с плоскостью АС образует нить на которой висит шарик?

4. В точке А, расположенной на расстоянии а=5 см от бесконечно длинной заряженной нити, напряженность электрического поля Е=150 кВ/м. При какой предельной длине l нити найденное значение напряженности будет верным с точностью до 2%, если точка А расположена на нормали к середине нити? Какова напряженность Е электрического поля в точке А, если длина нити l=20 см? Линейную плотность заряда на нити конечной длины считать равной линейной плотности заряда на бесконечно длинной нити. Найдите линейную плотность заряда на нити.

5. Найдите потенциал точки поля, находящейся на расстоянии r=10 см от центра заряженного шара радиусом R=1 см, поверхностная плотность заряда на шаре

6. Четверть тонкого кольца радиусом R=20 см. несет равномерно распределенный заряд Q=5 мкКл. Определите напряженность E и потенциал электрического поля, создаваемого этим зарядом в центре кривизны кольца.

7. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный электрический заряд с линейной плотностью мкКл/м. Найдите напряженность E электрического поля, созданного этим зарядом в точке, лежащей на оси стержня и удаленной на расстояние L=10 см от его начала.

8. Тонкий прямой стержень несет равномерно распределенный заряд Q= 100 нКл с линейной плотностью мкКл/м. Определите напряженность E и потенциал поля, создаваемого этим зарядом в точке, лежащей на оси стержня на расстоянии L=20 см от одного из его концов.

9. Кольцо радиусом r=5 см из тонкой проволоки равномерно заряжено с линейной плотностью  нКл/м. Определите напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние a=10 см от центра кольца.

10. По тонкому кольцу радиусом R=10 см равномерно рас­пределен заряд с линейной плотностью нКл/м. Определите потенциал в точке, лежащей на оси кольца на расстоянии а=5 см от центра.

11. На отрезке тонкого прямого проводника равномерно рас­пределен заряд с линейной плотностью нКл/м. Вычислите потенциал , создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.

12. Тонкая нить несет равномерно распределенный по длине заряд с линейной плотностью 2 мкКл/м. Вблизи средней части нити на расстоянии r=1 см, малом по сравнению с ее длиной, находится точечный заряд Q=0,1 мкКл. Определите силу F, действующую на заряд.

13. Очень длинная тонкая прямая проволока несет заряд, равномерно распределенный по всей ее длине. Вычислите линейную плотность  заряда, если напряженность E поля на расстоянии а=0,5 м от проволоки против ее середины равна 200 В/м.

14. Расстояние d между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью 150 мкКл/м. Какова напряженность Е поля в точке, удаленной на r=10 см как от первой, так и от второй проволоки?

15. Прямой металлический стержень диаметром d=5 см и длиной l=4 м несет равномерно распределенный по его поверхности заряд Q=500 нКл. Определите напряженность Е поля в точке, находящейся против середины стержня на расстоянии а=1 см от его поверхности.

16. Тонкий стержень длиной l=12 см заряжен с линейной плотностью =200 нКл/м. Найдите напряженность Е электрического поля в точке, находящейся на расстоянии r=5 см от стержня против его середины.

17. Т онкий стержень длиной l=10 см заряжен с линейной плотностью =400 нКл/м. Найдите напряженность Е электрического поля в точке, расположенной на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии r=8 см от этого конца.

18. Два прямых тонких стержня длиной l₁=12 см и l₂=16 см каждый заряжены с линейной плот­ностью =400 нКл/м. Стержни образуют прямой угол, как показано на рисунке 4. Найдите напряженность Е поля в точке А.

19. Электрическое поле создано зарядом тонкого равномерно заряженного стержня, изогнутого по трем сторонам квадрата (рисунок 5). Длина а стороны квадрата равна 20 см. Линейная плотность  зарядов равна 500 нКл/м. Вычислите напряженность Е поля в точке А.

20. Тонкий стержень длиной l=10 см равномерно заряжен. Линейная плотность  заряда равна 1 мкКл/м. На продолжении оси стержня на расстоянии а=20 см от ближайшего его конца находится точечный заряд Q=100 нКл. Определите силу F взаимодействия заряженного стержня и точечного заряда.

21. Тонкий длинный стержень равномерно заряжен с линейной плотностью  заряда, равной 10 мкКл/м. На продолжении оси стержня на расстоянии а=20 см от его конца находится точечный заряд Q=10 нКл. Определите силу F взаимодействия заряженного стержня и точечного заряда

22. Тонкий очень длинный стержень равномерно заряжен с линейной плотностью  заряда, равной 10 мкКл/м. На перпендикуляре к оси стержня, восставленном из конца его, находится точечный заряд Q=10 нКл. Расстояние а заряда от конца стержня равно 20 см. Найдите силу F взаимодействия заряженного стержня и точечного заряда

23. Т

    а/2

    онкая нить длиной l=20 см равномерно заряжена с линейной плотностью =10 нКл/м. На расстоянии а=10 см от нити, против ее середины, находится точечный заряд Q=1 нКл. Вычислите силу F, действующую на этот заряд со стороны заряженной нити

24. Тонкий длинный стержень равномерно заряжен с линейной плотностью =10 мкКл/м. Какова сила F, действующая на точечный заряд Q=10 нКл, находящийся на расстоянии а=20 см от стержня, вблизи его середины?

25. Тонкая бесконечная нить согнута под углом 90°. Нить несет заряд, равномерно распределенный с линейной плотностью =1 мкКл/м. Определите силу F, действующую на точечный заряд Q=0,1 мкКл, расположенный на .продолжении одной из сторон и удаленный от вершины угла на a=50 см

26. Тонкий стержень длиной l=30 см несет равномерно распределенный по длине заряд с линейной плотностью =1 мкКл/м. На расстоянии r₀=20 см от стержня находится заряд Q₁=10 нКл, равноудаленный от концов, стержня. Определите силу F взаимодействия точечного заряда с заряженным стержнем.

27. С какой силой на единицу площади отталкиваются две одноименно заряженные плоскости? Поверхностная плотность заряда на плоскостях мкКл/м

28. С какой силой F электрическое поле заряженной бесконечной плоскости действует на единицу длины заряженной бесконечно длинной нити, помещенной в это поле? Линейная плотность заряда нити мкКл/м, поверхностная плотность заряда плоскости

29. Две третьих тонкого кольца радиусом R=20 см несут равномерно распределенный отрицательный электрический заряд с линейной плотностью мкКл/м. Найдите напряженность Е и потенциал в центре кольца.

30. По тонкому кольцу радиусом R=10 см равномерно распределен электрический заряд с линейной плотностью мкКл/м. Определите напряженность Е и потенциал электрического поля, создаваемого этим зарядом, в точке лежащей на оси кольца на расстоянии вдвое большем его диаметра.

Задача 3. Электроемкость, конденсаторы

1. Расстояние d между пластинами плоского конденсатора равно 1,33 мм площадь S пластин равна 20 см². В пространстве меж­ду пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной d₁=0,7 мм и эбонита толщиной d₂=0,3 мм. Определите электроемкость с конденсатора

2. На пластинах плоского конденсатора равномерно распре­делен заряд с поверхностной плотностью σ=0,2 мкКл/м². Расстоя­ние d между пластинами равно 1 мм. На сколько изменится раз­ность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?

3. В плоский конденсатор вдвинули плитку парафина толщиной d=1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

4. Электроемкость с плоского конденсатора равна 1,5 мкФ. Расстояние d между пластинами равно 5 мм. Какова будет электроемкость С конденсатора, если на нижнюю пластину положить лист эбонита толщиной d₁=3 мм?

5. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка. Конденсатор заряжен до разности потенциалов U₁ = 100 В. Какова будет разность потен­циалов U ₂, если вытащить стеклянную пластинку из конденсатора?

6. К воздушному конденсатору, заряженному до разности потенциалов U=600 В и отключенному от источника напряжения, присоединили параллельно второй незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определите диэлектрическую проницаемость ε фарфора, если после присоединения второго конденсатора разность потенциалов уменьши­лась до U₁=100 В.

7. Конденсатор электроемкостью С₁=0,2 мкФ был заряжен, до разности потенциалов U₁=320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U₂=450 В, напряжение U на нем изменилось до 400 В. Вычислите емкость С₂ второго конденсатора.

8. Конденсатор электроемкостью С₁=0,6 мкФ был заряжен до разности потенциалов U₁=300 В и соединен со вторым конденсатором электроемко­стью С₂=0,4 мкФ, заряженным до разности потенциалов U₁=150 В. Найдите заряд ΔQ, перетекший с пластин первого конденсатора на второй.

9. Три одинаковых плоских конденсатора соединены после­довательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см². Диэлектрик - ­стекло. Какова толщина d стекла?

10. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r=10 см каждая. Расстояние d₁ между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U=1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d₂=3,5 см?

11. Плоский воздушный конденсатор электроемкостью С=1,11 нФ заряжен до разнести потенциалов U=300 В. После отключения от источника тока расстояние между пластинами конденсатора было увеличено в пять раз. Определите: 1) разность потен­циалов U на обкладках конденсатора после их раздвижения; 2) работу А' внешних сил по раздвижению пластин.

12. Конденсатор электроемкостью С₁=666 пФ зарядили до разности потенциалов U =1,5 кВ и отключили от источника тока. 3атем к конденсатору присоединили параллельно второй, незаря­женный конденсатор электроемкостью С₂=444 пФ. Определите энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

13. Конденсаторы электроемкостями С₁=1 мкФ, С₂=2 мкФ, С₃=3 мкФ включены в цепь с напряжением U =1,1 кВ. Определите энергию каждого конденсатора в случаях: 1) последовательного их включения; 2) параллельного включения.

14. Электроемкость С плоского конденсатора равна 111 пФ. Диэлектрик – фарфор ( ). Конденсатор зарядили до разности потен­циалов U=600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало.

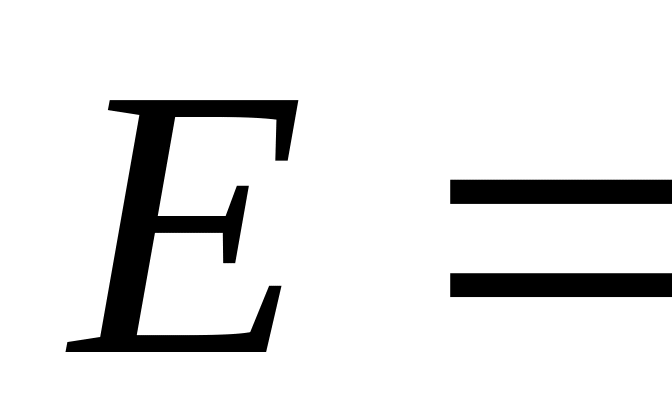15. К источнику с ЭДС 3 В подключили последовательно два плоских конденсатора, каждый емкости С=10 мкФ. Затем один из конденсаторов заполнили однородным диэлектриком с диэлектрической проницаемостью 5. Какой заряд пройдет через источник?

16. Конденсатор емкостью мкФ, предварительно заряженный до напряжения U=300 В, подключили параллельно к незаряженному конденсатору емкости мкФ. Найдите приращение внутренней энергии системы к моменту установления равновесия?

17. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S=100 . Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от 1 см до = 2 см, если при этом поддерживать неизменным заряд конденсатора Q=100 мкКл?

18. Имеется плоский воздушный конденсатор, площадь каждой обкладки которого равна S=100 . Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от см до =2 см, если при этом поддерживать неизменным напряжение на конденсаторе равным U=100В?

19. Плоский воздушный конденсатор, заряженный до разности потенциалов В, соединили с таким же по размерам конденсатором, но заполненным диэлектриком. Какова диэлектрическая проницаемость диэлектрика, если после соединения разность потенциалов между пластинами стала равна 100 В?

20. Плоский конденсатор с площадью каждой пластины S=200 и расстоянием между пластинами d=6 мм подключен к источнику постоянного напряжения U=100 В. Как изменится заряд на конденсаторе, если в него ввести пластинку толщиной с диэлектрической проницаемостью параллельно пластинам?

21. Конденсатор емкости мкФ, заряженный до разности потенциалов В, соединили параллельно с заряженным до разности потенциалов В конденсатором емкости мкФ (соединили одноименно заряженные обкладки конденсаторов). Какой заряд окажется на каждом из конденсаторов после соединения? Определите энергию, затраченную на образование искры в момент соединения конденсаторов?

22. Плоский воздушный конденсатор с расстоянием между обкладками d=2 см и площадью каждой из обкладок S=50 присоединен к источнику постоянного напряжения U=1 кВ. Параллельно пластинам конденсатора вносится металлическая пластинка толщиной d=1 см. Какую энергию расходует источник при внесении пластинки? Насколько изменится при этом энергия конденсатора?

23. Плоский воздушный конденсатор с площадью каждой из обкладок S=60 и расстоянием между обкладками d = 3 см заряжен до разности потенциалов 3000 В и отключен от источника напряжения. Параллельно обкладкам вносится металлическая пластинка толщиной вдвое меньше расстояния между ними. Какую работу совершат силы поля и каково будет изменение энергии конденсатора?

24. Конденсатор емкостью С=2 мкФ заполнен парафином и заряжен до разности потенциалов U=500 В и отключен от источника напряжения. Найдите работу A, которую надо совершить, чтобы достать диэлектрик из конденсатора?

25. Конденсатор емкостью мкФ зарядили до разности потенциалов В и отключили от источника тока. Определите разность потенциалов , установившуюся на этом конденсаторе после подключения к нему параллельно конденсатора емкостью мкФ. Определите энергию искры, проскочившей при соединении конденсаторов?

26. Внутри плоского конденсатора с площадью пластин S=200 и расстоянием между ними 0,1 см находится пластинка из стекла ( ), целиком заполняющая пространство между ними. Как изменится энергия конденсатора, если, не отключая конденсатор от батареи 300В, пластинку вынуть?

27. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом 10 см каждая. Расстояние между ними 1 см. Конденсатор зарядили до 1200В, и отключили от источника напряжения. Какую работу нужно совершить, чтобы увеличить расстояние между пластинами до 3,5 см?

28. Плоский воздушный конденсатор заряжен до разности потенциалов U=50 В и отключен от источника. После этого в конденсатор параллельно обкладкам вносится металлический лист толщиной =1мм. Найдите разность потенциалов между обкладками конденсатора, если расстояние между обкладками d=5мм? Площади обкладок и металлического листа равны

29. Плоский воздушный конденсатор заряжен до разности потенциалов U=60 В и отключен от источника электрического тока. После этого внутрь конденсатора параллельно обкладкам вводится пластинка из диэлектрика с диэлектрической проницаемостью 2. Толщина пластинки в два раза меньше величины зазора между обкладками конденсатора. Чему равна разность потенциалов между обкладками конденсатора после введения диэлектрика?

30. Два конденсатора с воздушным зазором, емкостью C=100 пФ каждый, соединены последовательно и подключены к источнику, ЭДС которого В. На сколько изменится заряд конденсаторов, если один из них погрузить в жидкий диэлектрик с диэлектрической проницаемостью 2?

ПОСТОЯННЫЙ ТОК

Основные формулы

• Сила постоянного тока

I=Q/t,

где Q - количество электричества, прошедшее сечение проводника за время t.

• Плотность электрического тока есть векторная величина, равная отношению силы тока к площади S поперечного сечения проводника:

где - единичный вектор, по направлению совпадающий с правлением движения положительных носителей заряда.

• Сопротивление однородного проводника

R=ρl/S,

где ρ - удельное сопротивление вещества проводника; l - его длина.

• Проводимость G проводника и удельная проводимость γ вещества

G=1/R, γ=l/ρ.

• Зависимость удельного сопротивления от температуры

ρ=ρ₀ (1+αt),

где ρ и ρ₀ - удельные сопротивления соответственно при t и 0 ˚С; t -температура (по шкале Цельсия); α - температурный коэффи­циент сопротивления.

• Сопротивление соединения проводников:

последовательного

параллельного

Здесь Ri - сопротивление i-го проводника; п - число провод­ников.

• Закон Ома:

для неоднородного участка цепи

для однородного участка цепи ;

для замкнутой цепи .

Здесь (φ₁-φ₂) - разность потенциалов на концах участка цепи; ε₁₂ - ЭДС источников тока, входящих в участок; U - напряжение на участке цепи; R - сопротивление цепи (участка цепи); ε - ­ЭДС всех источников тока цепи.

• Правила Кирхгофа. Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т. е.

где n - число токов, сходящихся в узле.

Второе правило: в замкнутом контуре алгебраическая сумма на­пряжений на всех участках контура равна алгебраической сумме электродвижущих сил, т.е.

где I_i - сила тока на i-м участке; R_i - активное сопротивление на i-м участке; ε_i - ЭДС источников тока на i-м участке; п - ­число участков, содержащих активное сопротивление; k- число участков, содержащих источники тока.

• Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t,

A=IUt;

• Мощность тока

P=IU.

• Закон Джоуля - Ленца

Q=I²Rt,

где Q - количество теплоты, выделяющееся в участке цепи за время t;

Закон Джоуля - Ленца справедлив при условии, что участок цепи неподвижен и в нем не совершаются химические превращения.

Примеры решения задач

Пример 1. Источники тока с электродвижущими силами ε₁ и ε₂ включены в цепь, как показано на рисунке (см. далее). Определите силы токов, текущих в сопротивлениях R₂ и R₃, если ε₁=10 В и ε₂=4 В, а R₁=R₄=20м и R₂=R₃=4 Ом? Сопротивлениями источников тока пренебречь.

Решение. Силы токов в разветвленной цепи определяют с помощью законов Кирхгофа. Чтобы найти четыре значения силы токов, следует составить четыре уравнения.

Указание. Перед составлением уравнений по закону Кирхгофа необхо­димо, во-первых, выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже, и, во-вторых, выбрать на­правление обхода контуров (последнее только для составления уравнений по второму закону Кирхгофа).

Выберем направления токов, как они показаны на рисунке, и условимся обходить контуры по часовой стрелке.

Рассматриваемая в задаче схема имеет два узла: А и В. Но состав­лять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.При составлении уравнений по первому закону Кирхгофа необ­ходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, - со знаком минус.

По первому закону Кирхгофа для узла В имеем

I₁+I₂+I₃-I₄=0.

Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составле­ны по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы Найдите необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовав­шая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необ­ходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлени­ем обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в противном случае произведение IR входит в уравнение со знаком минус,

б) если ЭДС повышает потенциал в направлении обхода контура, т.е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае - со знаком минус.

По второму закону Кирхгофа имеем соответственно для контуров AR₁BR₂A, AR₁BR₃A, AR₃BR₄A:

I₁R₁ - I₂R₂=ε₁ - ε₂ (1)

I₁R₁- I₃R₃= ε₁ (2)

I₃R₃ + I₄R₄=0. (3)

Подставив в равенства (1)-(3) значения сопротивлений и ЭДС, получим систему уравнений:

I₁+I₂+I₃-I₄=0,

2I₁-4I₂=6,

2I₁-4I₃=10,

4I₃+2I₄=0.

Поскольку нужно найти только два тока, то удобно воспользо­ваться методом определителей (детерминантов). С этой целью пере­пишем уравнения еще раз в следующем виде:

I₁+I₂+I₃-I₄=0,

2I₁-4I₂+0+0=6,

2I₁+0-4I₃+0=10,

0+0+4I₃+2I₄=0.

Искомые значения токов найдем из выражений

I₂=Δ_I2/Δ и I₃=Δ_I3/Δ,

где Δ - определитель системы уравнений; Δ_I2 и Δ_I3 - определители, полученные заменой соответствующих столбцов определителя А столбцами, составленными из свободных членов четырех вышеприведенных уравнений, находим

Отсюда получаем

I₂=0; I₃ = -1 А.

Знак минус у значения силы тока I₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, направление тока I₃ было указано противоположно истинному. На самом деле ток I₃ течет от узла В к узлу А.

Пример 2. Сила тока в про­воднике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному за. кону от I₀=0 до I_max=6 А (рис. 19.3). Определите количество теплоты Q₁, выделившееся в этом проводнике за первую секунду, и Q₂ - за вторую, а также найти отношение этих количеств теплоты Q₂/Q₁.

Решение. Закон Джоуля - Ленца Q= I²Rt применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

dQ= I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В на­шем случае

I=kt, (2)

где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:

k=ΔI/Δt.

С учетом равенства (2) формула (1) примет вид

dQ=k²Rt²dt. (3)

Для определения количества теплоты, выделившегося за конечный промежуток времени Δt, выражение (3) следует проинтегрировать в пределах от t₁ до t₂:

При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t₁ =О, t₂= 1 с и, следовательно,

Q₁=60 Дж,

а за вторую секунду - пределы интегрирования t₁= 1 с, t₂=2 с и тогда

Q₂=420 Дж.

Следовательно,

Q₂/Q₁=7,

т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду