3.4. Аналитические модели

Третьей типовой математической моделью ОД является анали­тическая модель. Объект, согласно этой модели, в общем виде будет описываться системой нелинейных дифференциальных уравнений

dx_i/dt= f_i (t, 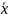, 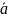)= 1N, (1)

где 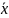— вектор переменных модели; — вектор параметров модели; f₁ — нелинейная функция времени, параметров и переменных. Ре­шение задач поиска дефектов по аналитическим моделям предпола­гает исследование процессов изменения коэффициентов и структу­ры выражения, связанных с конструктивными параметрами ОД по известным входным

X(t) и выходным Y(t) сигналам. Эта задача, в общем случае, решается в три этапа: по измеренным величинам Y(t) и известной структуре функций f₁ оцениваются параметры 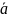; по другим параметрам формируются признаки элементов множества воз­можных дефектов; по эталонным и текущим признакам выводится суждение о наличии дефекта(ов). Задача первого этапа — это ти­пичная задача параметрической идентификации. Бурное развитие теории и практики идентификации позволили получить большое число

4

различных модификаций модели для широкого класса техни­ческих объектов

в виде операторных, векторных, матричных, диф­ференциальных и алгебраических уравнений. Все эти математиче­ские описания привлекают в качестве диагностических моделей для разработки и использования кибернетических методов решения за­дачи поиска дефектов.

Измерение исходных диагностических -показателей (парамет­ров, характеристик) осуществимо в статических и динамических ре­жимах работы ОД. В зависимости от режима измерений аналитиче­ские модели, описывающие ОД, в этих режимах, делят на статиче­ские и динамические.

Методы поиска дефектов с использованием статических анали­тических моделей (системы алгебраических уравнений) принципи­ально приводят к неполноте диагноза, так как объекты по своей природе являются динамическими, и, в общем случае, существует непустое подмножество множества возможных дефектов, элементы которого объективно проявляются только в динамических режимах функционирования ОД. Поэтому для определенных классов ОД (например САУ, промышленные роботы) статические модели не эффективны.

Этот факт, и, кроме того, чрезвычайно большая информатив­ность динамических режимов в сравнении со статическими, обу­словливает необходимость использования для динамических ОД (объектов, для которых динамические свойства являются определя­ющими свойствами) математического описания в виде аналитиче­ских динамических моделей.

3.5. Информационные модели

Очевидно, что система технического диагностирования может быть представлена как источник информации о техни­ческом состоянии объекта, на основе которой осуществляется управление состоянием. Естественно, что возможности информаци­онных описаний приводят к построению особого класса моделей диагностирования - информационных моделей. Используя теорию информации можно в требуемом объеме описать ОД, как датчик, измерительные приборы, так и преобразователи информа­ции средства отображения информации, а также и само диагности­рование, как процесс снятия неопределенности или энтропии при определении работоспособного состояния объекта поиска и нахож­дения места отказа.

Самым главным преимуществом информационных моделей диагностирования является единство математического аппарата, описывающего различные объекты и процессы, что позволяет про­явить их информационная сущность. Это позволяет, используя ин­формационную модель, связать в единое целое самые различные параметры СТД и рассматривать их взаимовлияние.

С информационной точки зрения ОД — датчик ДП, имеющего среднеквадратическое значение σ_х². Измерительный прибор СТД характеризуется среднеквадратической погрешностью и полосой пропускания W. Количество информации, полученное при

5

диагностировании

I = WT log₂(σ_х² + σ_П²)/ σ_П² . (2)

Учитывая неравенство неравенство

σ_x² 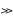σ_П² количество информации диагностирования

I=2WTlog₂σ_x /σ_П. (3)

Работа СТД ограничена во времени возможностью отказа. Среднее время безотказной работы системы в течение периода Т:

T₁ = T₀ (1 - p) (4)

где T₀ = 1/ λ — средняя наработка на отказ, λ — параметр потока отказов, а величина р=е^-λt — вероятность безотказной работы. Таким образом, сокращение времени работы СТД за счет возмож­ного отказа можно рассматривать как уменьшение информации о состоянии. Информационные потери можно определить из вы­ражения

ΔI = I – I₁ = 2W [ Т — Т₀(1— p)] Iog₂(σ_x /σ_П). (1-12)

Исходя из положений теории информации, потери необходимо рассматривать как увеличение среднеквадратической погрешности прибора до величины σ₃ /σ_π. Важно отметить, что количество

информации зависит от точности, безотказности, полосы пропуска­ния и является комплексным показателем качества СТД.

В общем случае информационные модели объекта диагностиро­вания можно рассматривать как частные случаи моделей планиро­вания эксперимента. Главная задача в конечном счете получать максимум информации о состоянии при наименьших затратах (по­терях) времени и средств.

6