Стоячие электромагнитные волны
При наложении двух бегущих волн с одинаковыми частотами и амплитудами, распространяющихся навстречу друг другу, образуется колебательное состояние – стоячая волна.
Для
электрической составляющей E
электромагнитной волны уравнение
стоячей волны определяется формулой:
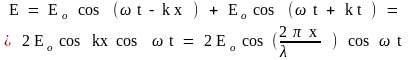, (29)
где
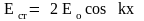– амплитуда стоячей волны, зависящая
от координаты точки наблюдения
;
–
волновое
число.
Волновое
число
определяет
число длин волн
,
которое укладывается на расстоянии
:
,
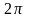где – длина волны;
–
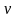скорость
волны;
– циклическая частота колебаний источника.
Амплитуда
колебаний напряженности электрического
поля достигает максимального значения;
равного
.
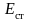в точках среды, где выполняется условие
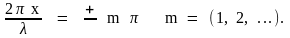(30)
Амплитуда
колебаний вектора напряженности
электрического поля
обращается в нуль в точках среды, где
выполняется условие
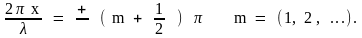(31)
Точки среды, в которых амплитуда максимальна (30), называются пучностями стоячей волны. Точки среды, в которых амплитуда колебаний равна нулю (31), называются узлами стоячей волны. Точки среды, находящиеся в узлах, неподвижны.
В
бегущей волне электрическая составляющая
и магнитная составляющая
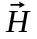имеют одинаковые фазы (рис. 1.)
Однако в стоячей волне между колебаниями составляющих и существует разность фаз. Пучности напряженности электрического поля не совпадают с пучностями напряженности магнитного поля, и наоборот.
Причина
возникновения разности фаз заключается
в том, что
при возникновении обратной волны фаза
колебаний должна измениться на
только одной составляющей: либо
напряженности электрического поля
,
либо напряженности магнитного поля
.
Взаимная ориентация векторов электрической и магнитной составляющих электромагнитной волны представлена на рис. 2.
Рис. 2. Взаимная ориентация электрической и магнитной составляющих электромагнитной волны: а) - для бегущей волны; б) - для волны, отраженной от открытой линии; в) - для волны, отраженной от замкнутой линии
Из
уравнения вектора Умова-Пойтинга (28)
следует, что вектора
,
и
бегущей волны составляют правую тройку
векторов (рис. 2а). При отражении направление
скорости волны
изменяется на обратное, поэтому, чтобы
сохранилась правая тройка векторов,
одна из составляющих
или
должна изменить свое направление на
противоположное (рис. 2б, в).
Распределение амплитуд электрического и магнитного полей показано на рис. 3. В стоячей электромагнитной волне узлы электрического поля (напряжения) совпадают с пучностями магнитного поля (тока) и наоборот. В этом случае пучности электрической и магнитной составляющих электромагнитной волны смещены друг относительно друга на четверть длины волны.
Рис. 3. Распределение амплитуд электрического и магнитного полей
в стоячей электромагнитной волне