
- •Техника безопастности
- •Основы теории максвелла для электромагнитного поля
- •Уравнения максвелла для электромагнитного поля
- •Электромагнитные волны
- •Стоячие электромагнитные волны
- •Стоячие электромагнитные волны в двухпроводной линии
- •Порядок выполнения работы Задание 1. Измерить длину стоячей волны в замкнутой двухпроводной линии
- •Задание 2. Измерить длину стоячей волны в открытой на одном конце двухпроводной линии
- •Контрольные вопросы
- •Библиографический список
Электромагнитные волны
Электромагнитные волны – это электромагнитное поле, изменяющееся в пространстве и времени.
Плоская монохроматическая электромагнитная волна (электромагнитная волна одной строго определенной частоты) описывается следующими уравнениями:
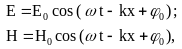 (21)
(21)
где
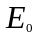 и
и
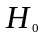 –
соответственно амплитуды напряженностей
электрического и магнитного полей
волны;
–
соответственно амплитуды напряженностей
электрического и магнитного полей
волны;
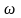 –
круговая
частота волны;
–
круговая
частота волны;
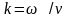 – волновое
число;
– волновое
число;
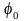 –
начальная
фаза колебаний.
–
начальная
фаза колебаний.
Начальная
фаза
характеризует
значения напряженности электрического
поля
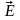 и
напряженности магнитного поля
в точке с координатой
и
напряженности магнитного поля
в точке с координатой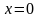 в момент времени
в момент времени
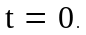
Электромагнитные
волны поперечны, т.е. векторы
и
взаимно
перпендикулярны и лежат в плоскости,
перпендикулярной вектору скорости
распространения волны
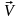 .
Векторы
,
и
образуют
правовинтовую систему (см. рис. 1).
.
Векторы
,
и
образуют
правовинтовую систему (см. рис. 1).

Рис. 1. Мгновенный снимок электромагнитной волны
Из уравнений Максвелла следует, что в бегущей электромагнитной волне векторы и колеблются в одинаковых фазах. Мгновенные значения векторов напряженности электрического поля и напряженности магнитного поля в любой точке связаны соотношением
 .
(22)
.
(22)
Распределения максимумов и минимумов амплитуд бегущей электромагнитной волне показана на рис. 1. Составляющие электромагнитной волны и одновременно достигают максимума и одновременно обращаются в нуль.
Фазовая скорость электромагнитных волн определяется выражением
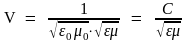 ,
(23)
,
(23)
где
 –
электрическая постоянная;
–
электрическая постоянная;
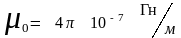 – магнитная
постоянная;
– магнитная
постоянная;
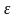 и
и
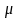 –
относительная диэлектрическая и
относительная магнитная проницаемость
среды, соответственно;
–
относительная диэлектрическая и
относительная магнитная проницаемость
среды, соответственно;
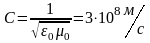 – скорость
света в вакууме.
– скорость
света в вакууме.
Расстояние между точками, колеблющимися в одинаковой фазе, определяет длину волны:
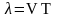 ,
(24) где
,
(24) где
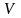 –
фазовая скорость волны;
–
фазовая скорость волны;
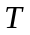 –
период
колебаний источника.
–
период
колебаний источника.
Основным свойством электромагнитных волн является перенос энергии, поэтому их можно обнаружить в точке наблюдения по изменению энергии.
Объемная
плотность
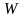 энергии электромагнитной волны
складывается из объемных плотностей
электрического
энергии электромагнитной волны
складывается из объемных плотностей
электрического
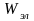 и магнитного
и магнитного
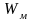 полей:
полей:
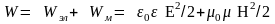 .
(25)
.
(25)
С
учетом того, что в каждый момент
времени
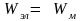 , уравнение (25)рпмет вид:
, уравнение (25)рпмет вид:
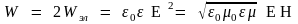 .
(26)
.
(26)
Потоком энергии называется величина, численно равная количеству энергии, переносимой волной за единицу времени через единицу площади, перпендикулярной к направлению распространения волны.
С учетом формулы (23) уравнение (26) преобразуется к виду:
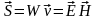 ,
(27)
,
(27)
где
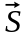 –
вектор плотности потока энергии.
–
вектор плотности потока энергии.
Учитывая направление векторов , и (рис. 1), формулу (27) можно записать в следующем виде:

(28)
Следовательно,
вектор плотности потока энергии
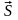 определяется
векторным произведением векторов
и
.
определяется
векторным произведением векторов
и
.
Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойтинга. Вектор направлен в сторону распространения электромагнитной волны, а модуль его равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению распространения волны.
Простейшим излучателем электромагнитных волн является электрический диполь, дипольный момент которого изменяется во времени по гармоническому закону. Задача об излучении диполя в теории излучающих систем имеет важное значение, т.к. всякую реальную излучающую систему (например: антенну) можно рассчитать, рассматривая ее как систему многих диполей определенной конфигурации.
