5. Виды движения точки в зависимости от ускорения

Рассмотрим возможные случаи движения точки и проанализи­руем выведенные выше формулы для касательного и нормального ускорений.

Равномерное прямолинейное движение характеризуется тем, что скорость движения точки М постоянна (v = const), а ра­диус кривизны траектории ее движения равен бесконечности (рис. а). В этом случае касательное ускорение равно нулю, так как модуль скорости не изменяется (v = const),

a_t= d_v/ d_t= 0.

Нормальное ускорение также равно нулю (r = ∞)

а_п = v²/r = 0.

Значит, и полное ускорение движения точки равно нулю а = 0.

Равномерное криволинейное движение характеризуется тем, что численное значение скорости постоянно (v = const), ско­рость меняется лишь по направлению. В этом случае касатель­ное ускорение равно нулю, так как v = const (рис. б),

a_t= d_v/ d_t= 0.

а нормальное ускорение не равно нулю (a_n= v²/r ≠ 0), так как r — конечная величина.

Полное ускорение при равномерном криволинейном движении равно нормальному ускорению, т. е. а = а_п.

Неравномерное прямолинейное движение характеризуется тем, что численное значение скорости движения точки (рис. 120, в) изменяется (v ≠ const), а радиус кривизны траектории движе­ния точки г равен бесконечности (r = ∞). Поэтому касательное ускорение здесь не равно нулю

a_t= d_v/ d_t ≠ 0.

а нормальное ускорение равно нулю

а_п = v ²/r = 0 (r = ∞).

Следовательно, полное ускорение точки при неравномерном пря­молинейном движении равно касательному ускорению, т. е.

а = a_t.

Неравномерное криволинейное движение (рис. 129, г) характери­зуется тем, что численное значение скорости движения точки М изменяется (v ≠ const), а радиус кривизны траектории ее движе­ния — конечная величина. В этом случае касательное ускорение не равно нулю

a_t= d_v/ d_t ≠ 0.

и нормальное ускорение также не равно нулю

а_п = v ²/r ≠ 0

Следовательно, полное ускорение при неравномерном криво­линейном движении складывается геометрически из касательного и нормального ускорений, т. е.

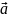= _t + _n

Когда значение касательного ускорения постоянно (a_t = const), движение точки называется равнопеременным. Равнопеременное движение может быть равномерно-ускоренным и равномерно-за­медленным, в зависимости от того, увеличивается или уменьшается численное значение скорости. Ускорения можно определить через значения скорости в начале и в конце произвольного проме­жутка времени

A_t = v – v₀ / t

откуда

v = v₀ + a_t t,

При равномерно-ускоренном движении ускорение a_t считается положительным, а при равномерно-замедленном — отрицатель­ным.

Перемещение точки при равнопеременном движении опреде­ляется по уравнению

Примером равномерно-ускоренного движения может служить свободное падение тела. Ускорение свободного падения обозна­чается буквой g. Опытом установлено, что это ускорение составляет вблизи поверхности Земли в среднем 9,81 м/с².