
- •1.Шеңберге жүргізілген жанама туралы есеп.
- •2. Эллипске жүргізілген жанама туралы есеп.
- •3. Потенциалдық энергияның минимумдық принципі.
- •4. Екі материалдық нүктенің ауырлық центрі.
- •5. Химиялық есептерді шешуде геометриялық әдісті пайдалану.
- •6. Кейбір геометриялық теоремалардың механикалық мағынасы.
- •Қолданылған әдеиеттер.
4. Екі материалдық нүктенің ауырлық центрі.
Массамен
қамтамасыз етілген нүкте материалдық
нүкте деп аталады. Көрнекті түрде
материалдық нүктені мөлшерін ескермеуге
болатын кішкене ауыр шарик түрінде
елестетуге болады. Егер
нүктесінде
 массасы орналасқан материалдық нүктені
массасы орналасқан материалдық нүктені
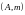 түрінде белгіленеді.
түрінде белгіленеді.
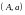 және
және
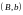 материалдық нүктелерінің ауырлық центрі
деп
материалдық нүктелерінің ауырлық центрі
деп
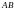 кесіндісінде жатып, «рычаг ережесін»
қанағаттандыратын
кесіндісінде жатып, «рычаг ережесін»
қанағаттандыратын
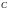 нүктесін айтады:
нүктесін айтады:
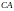 қашықтығын
нүктесінің массасы
қашықтығын
нүктесінің массасы
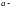 ға көбейтіндісі
ға көбейтіндісі
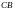 қашықтығының
қашықтығының
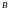 нүктесінің массасы
нүктесінің массасы
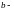 ға
көбейтіндісіне тең. Сонымен,
ға
көбейтіндісіне тең. Сонымен,
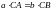
Бұл теңдікті былай да жазуға болады:
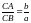 ,
,
яғни, екі нүктенің ауырлық центрінен осы нүктелерге дейінгі қашықтықтардың қатынасы олардың массаларының қатынасына кері пропорционал болады. және материалдық нүктелерінің ауырлық центрі нүктесі болады дегенді былай белгілейді:
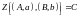 .
.
Ауырлық центрі массасы үлкен нүктеге жақын орналасады. Анықтамадан егер түзу екі нүктенің ауырлық центрі мен осы нүктелердің біреуі арқылы өтсе, онда ол екінші нүкте арқылы да өтеді.
Екі
нүктенің ауырлық центрінің механикалық
мағынасы өте қарапайым. Екі ұшына
 және
және
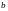 масса орналастырылған «салмақсыз»
стерженін
елестетейік.
және
материалдық нүктелерінің ауырлық центрі
деп, осы нүктеден тіреу қойғанда, ол
тепе тең қалыпта болатын
нүктесін айтады.
масса орналастырылған «салмақсыз»
стерженін
елестетейік.
және
материалдық нүктелерінің ауырлық центрі
деп, осы нүктеден тіреу қойғанда, ол
тепе тең қалыпта болатын
нүктесін айтады.

11-сурет
Екі материалдық нүктенің бірігуі немесе тең әсердесуі деген ұғымдарды қолданамыз. Бұл ұғымдар ретінде екі материалдық нүктенің ауырлық центріне олардың массаларының қосындысын орналастыруды айтады.
Мысалы,
ұзындығы 20 см. болатын
стерженінің ұштары
нүктесіне 6 бірлік,
нүктесіне
6 бірлік массалар орналастырылсын.
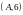 және
және
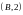 нүктелерінің ауырлық центрі
мына шартты қанағаттандырады:
нүктелерінің ауырлық центрі
мына шартты қанағаттандырады:
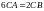 немесе
немесе
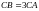 .
Сонымен қатар
.
Сонымен қатар
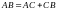 болғандықтан
болғандықтан
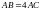 болады.
Бұдан
болады.
Бұдан
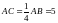 (бірлік).
(бірлік).
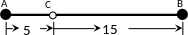
12-сурет
және
материалдық нүктелерінің бірігуі
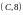 материалдық нүктесі болады.
материалдық нүктесі болады.
Үш материалдық нүктенің ауырлық центрі былайша тізбектей табылады: алдымен кез келген екі нүктенің ауырлық центрін тауып, осы нүкте мен үшінші нүктенің ауырлық центрін табады. Дәл осылайша төрт, бес т.с.с. нүктелердің ауырлық центрін табады.
Мысалы,
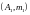 ,
,
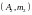 ,
,
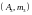 ,
,
 нүктелерінің ауырлық центрін табу
керек.
нүктелерінің ауырлық центрін табу
керек.
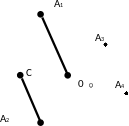
13-сурет
және
нүктелерінің ауырлық центрі
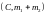 нүктесі болады. Енді
,
,
үш нүктенің ауырлық центрін жоғарыдағыдай
табамыз. Сонда
нүктесі болады. Енді
,
,
үш нүктенің ауырлық центрін жоғарыдағыдай
табамыз. Сонда
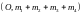 нүктесі шығады.
нүктесі шығады.
Енді осы айтылғандарды геометриялық есептерді шешуде қолданайық.
Мысал-1. Кез келген төртбұрыштың орта сызығы деп оның қарама-қарсы қабырғаларының ортасын қосатын кесіндіні айтады.
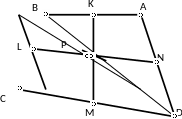
14-сурет
Мына теореманы дәлелдейік. Кез келген төртбұрыштың орта сызықтары мен диагональдарының ортасын қосатын кесінді бір нүкте арқылы өтеді және осы нүктеде қақ бөлінеді.
Дәлелдеуі.
 төртбұрышының әр төбесіне бір бірліктен
масса орналастырайық. Осы төрт материалдық
нүктенің ауырлық центрін
деп белгілейік.
және
нүктелеріндегі массаны олардың ауырлық
центрі
төртбұрышының әр төбесіне бір бірліктен
масса орналастырайық. Осы төрт материалдық
нүктенің ауырлық центрін
деп белгілейік.
және
нүктелеріндегі массаны олардың ауырлық
центрі
 нүктесіне, ал
және
нүктесіне, ал
және
 нүктелеріндегі массаны олардың ауырлық
центрі
нүктесіне орналастырсақ, одан жүйенің
ауырлық центрінің орны өзгермейді.
және
нүктелерінде
массалар тең болғандықтан,
нүктелеріндегі массаны олардың ауырлық
центрі
нүктесіне орналастырсақ, одан жүйенің
ауырлық центрінің орны өзгермейді.
және
нүктелерінде
массалар тең болғандықтан,
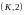 және
және
 нүктелерінің ауырлық центрі
нүктелерінің ауырлық центрі
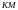 кесіндісінің
ортасы
нүктесі болады да оны қақ бөледі. Дәл
осылайша
нүктесі
кесіндісінің
ортасы
нүктесі болады да оны қақ бөледі. Дәл
осылайша
нүктесі
 және
және
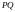 кесінділерінде жатып, оларды қақ
бөлетінін көрсетеміз. Сонымен,
,
,
кесінділері ортақ
нүктесі арқылы өтіп, осы нүктеде қақ
бөлінеді. Теорема дәлелденді.
кесінділерінде жатып, оларды қақ
бөлетінін көрсетеміз. Сонымен,
,
,
кесінділері ортақ
нүктесі арқылы өтіп, осы нүктеде қақ
бөлінеді. Теорема дәлелденді.
Мысал-2. Геометриядан белгілі мына теореманы дәлелдейік. Кез келген үшбұрыштың үш медианасы бір нүктеде қилысады және қилысу нүктесінде төбесінен есептегенде 2:1 қатысында бөлінеді.
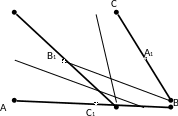
15-сурет
Дәлелдеуі.
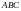 үшбұрышының әр төбесіне бір бірлік
массадан орналастырайық
(сурет15 ).
нүктесі берілген жүйенің ауырлық центрі
болсын.
үшбұрышының әр төбесіне бір бірлік
массадан орналастырайық
(сурет15 ).
нүктесі берілген жүйенің ауырлық центрі
болсын.
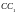 кесіндісі үшбұрыштың бір медианасы.
кесіндісі үшбұрыштың бір медианасы.
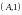 және
және
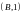 материалдық нүктелерінің массаларын
кесіндісінің ортасы болатын
материалдық нүктелерінің массаларын
кесіндісінің ортасы болатын
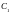 нүктесіне шоғырландырайық. Сонда барлық
жүйе
нүктесіне шоғырландырайық. Сонда барлық
жүйе
 және
және
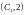 нүктелерінен тұрады. Жүйенің ауырлық
центрі
нүктесі
кесіндісінде жатады. Дәл осылайша
нүктесі
нүктелерінен тұрады. Жүйенің ауырлық
центрі
нүктесі
кесіндісінде жатады. Дәл осылайша
нүктесі
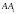 және
және
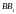 медианаларында жататынын көрсетуге
болады. Сонымен, үшбұрыштың барлық
медианасы бір нүкте арқылы өтеді. Рычаг
ережесі бойынша
медианаларында жататынын көрсетуге
болады. Сонымен, үшбұрыштың барлық
медианасы бір нүкте арқылы өтеді. Рычаг
ережесі бойынша
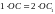 ,
яғни
,
яғни
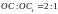 .
Теорема дәлелденді.
.
Теорема дәлелденді.
Мысал-3.
үшбұрышының
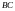 ,
,
қабырғаларынан сәйкес
,
,
қабырғаларынан сәйкес
 ,
,
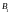 ,
нүктелері
,
нүктелері
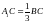 ,
,
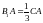 ,
,
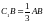 теңдіктері орындалатындай етіп алынған.
,
,
нүктелерін қарама-қарсы
,
,
нүктелерімен қосатын түзулер берілген
үшбұрышты жеті бөлікке бөледі. 16 –
суреттегі штрихталған үшбұрыштың ауданы
үшбұрышының ауданынан жеті есе кіші
екенін дәлелдеу керек.
теңдіктері орындалатындай етіп алынған.
,
,
нүктелерін қарама-қарсы
,
,
нүктелерімен қосатын түзулер берілген
үшбұрышты жеті бөлікке бөледі. 16 –
суреттегі штрихталған үшбұрыштың ауданы
үшбұрышының ауданынан жеті есе кіші
екенін дәлелдеу керек.
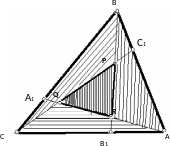
16-сурет
Дәлелдеуі.
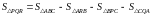 болатынын 16- суреттен көруге болады.
Егер екі үшбұрыштың биіктіктері бірдей
болса, онда олардың аудандарының қатынасы
сәйкес табандарының ұатынасына тең
болатыны белгілі, яғни
болатынын 16- суреттен көруге болады.
Егер екі үшбұрыштың биіктіктері бірдей
болса, онда олардың аудандарының қатынасы
сәйкес табандарының ұатынасына тең
болатыны белгілі, яғни
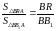 .
.
нүктесі
үш материалдық нүктенің ауырлық центрі
болатындай етіп,
үшбұрышының төбелеріне массалар
орналастырайық. Ол үшін
,
,
төбелеріне сәйкес 1, 2, 4 бірлік масса
орналастыру жеткілікті.
 және
және
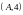 материалдық нүктелерін олардың бірігуі
болатын
материалдық нүктелерін олардың бірігуі
болатын
 нүктесімен алмастырамыз. Сонда
нүктесі
және
материалдық нүктелерінің ауырлық центрі
болады. Рычаг ережесі бойынша
нүктесімен алмастырамыз. Сонда
нүктесі
және
материалдық нүктелерінің ауырлық центрі
болады. Рычаг ережесі бойынша
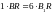 болады. Бұдан
болады. Бұдан
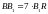 және
және
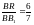 .
Сонымен,
.
Сонымен,
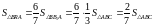 .
.
Дәл
осылайша
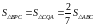 болатынын көрсете аламыз. Сондықтан
болатынын көрсете аламыз. Сондықтан
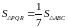 .
.
