Кіріспе

Қазақстан Республикасының президенті Н.Ә.Назарбаевтың Қазақстан халқына арналған жолдауында «...Біздің болашақтың жоғары технологиялық және ғылыми қамтылатын өндірістері үшін кадрлар қорын жасақтауымыз қажет...» деген сөзі бар. Болашақта сол кадрлар қатарына тұрудың негізгі шарттарының бірі - математиканы терең меңгеру деп білемін.

Мен үшін мектептегі оқылатын пәндердің ішіндегі ең негізгісі - математика. Математика нақты дәлелдеуді қажет ететін, қызықты да қиын пән. Өмір өзі есептеуден тұрады. Туғаннан дене салмағын, бойдың ұзындығын өлшеуден бастап, адам дамуының негізгі есептеулері басталады.

Математиканың негізгі бір саласы – геометрия. «Геометрия» атауының дәл аудармасы «жер өлшеу» болады. Бұл ғылымның негізі Ежелгі Мысыр елінен шыққан. Геометрияның заңдылықтарын жер өлшеу мәселесіне толық қолдануға болады. Бірақ геометрияның негізгі арнасы ол емес. Геометрия қолданылатын мәселелер сан алуан. Сондықтан геометрия ерте заманның өзінде жазықтықтағы және кеңістіктегі пішіндердің, денелердің арасындағы қатынастар мен ұқсастықтарды зерттеп, ғылым ретінде қалыптасты.

Зерттеу жұмысының өзектілігі. Геометрия тек жер өлшеу жұмыстарында емес, үй, көпір, әскери бекіністер, су арналарын қазу, ыдыстың сиымдылығын өлшеу, әр түрлі құрлыс жұмыстарына қажетті материалдардың шамасын алдын ала есептеу, т.б. жұмыстарда кең қолданылады.

Геометрия жаратылыстану ғылымдарында кең қолданыс тапты. Физикалық денелерді зерттеу барысында олардың температурасын, массасын, тығыздығын, т.с.с. қасиеттерін дерексіздендіріп қарастыру арқылы физикалық заңдылықтардың ашылуына үлкен үлес қосты. Астрономия саласындағы зерттеулер тікелей геометриялық заңдылықтардың негізінде зерттелуде.

Жаратылыстану ғылымының тағы бір саласы – химия. Бірнеше компоненттерден тұратын химиялық қоспаларды материалдық нүкте арқылы сипаттау тікелей геометриялық заңдылықтарға бағынады. Сонымен қатар химиялық қоспалардың компоненттерінің концентрацияларын анықтау және керісінше, берілген концентрациялары арқылы қоспаны сипаттайтын нүктені табу есебінің химиялық зерттеуде маңызы зор.

Зерттеу жұмысының мақсаты. Жаратылыстану ғылымдары пәндері – физика мен химияның есептерін геометриялық әдістерді пайдаланып шығару.

Зерттеу жұмысының міндеттері:

• Шеңберге жүргізілген жанама туралы есепті қарастыру;

• Эллипске жүргізілген жанама туралы есепті қарастыру;

• Потенциалдық энергияның минимумдық принципін баяндау;

• Екі және бірнеше материалдық нүктенің ауырлық центрі туралы есепті қарастыру.

Физиканың, химияның, механиканың есептерін шешуде геометрияны қолдану, есептің көрнекілігін айқындайды. Физикадағы «ауырлық центрі» қоғымының геометриялық мағынасын ашуға, оны қолдануға өмірде жиі кездесетін есептер қарастырылды.

Зерттеу жұмысының нәтижесі: Осы зерттеу жұмысымен шұғылдану барысында мен геометрия курсының кейбір теоремаларының химиялық, физикалық мағыналарын, оларды дәлелдеуде геометриялық әдістерді қолдануды меңгердім. Жүктің тепе теңдік қалпын, потенциалдық энергияның ең кіші мәнін, қоспаның концентрациясын математикалық есептерді шешуге қолданып, оған өмірден алынған мысалдарды қарастырдым.

Бірнеше компоненттерден тұратын химиялық қоспаларды геометриялық сипаттаудың маңызы ерекше және оны сипаттайтын нүктенің геометриялық фигуралардың ауырлық центрімен байланысын қарастырдым. Гиббстің үшбұрышты диаграмасын қолданып практикалық есептер шығарылды.

Геометриядағы «жанама туралы» есептердің механикалық мағынасына ерекше көңіл аудардым. Бұл есеп шеңбер және эллипс үшін қарастырылды.

Мекпепте оқытылатын геометрия курсының қолдану аясының өте кең екендігіне, жаратылыстану ғылымдарының есептерін геометрия тіліне аударып, геометриялық фигуралардың арасындағы қатынастары, олардың ұқсастықтарының геометриялық белгілерін қолданудың тиімді екеніне көз жеткіздім.

1.Шеңберге жүргізілген жанама туралы есеп.

Шеңбермен бір ғана ортақ нүктесі болатын түзу шеңберге жанама түзу деп аталатыны белгілі.Осы ортақ нүкте жанасу нүктесі деп аталады. Геометрия оқулығында «жанасу нүктесінде шеңбердің радиусы жанамаға перпендикуляр болады» деген теорема дәлелденген. Осы теореманың дәлелдеуін механикалық тұрғыдан келтірейік.

Осы мақсатта ойша мынандай эксперимент жүргізейік: жіптің 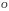ұшы бекітілген, ал екінші 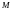ұшында жүк ілінген. Күнделікті тәжірибеден мына тұжырымның дұрыс екенін көреміз.

(А) Ілінген жүк жіпке қатысты өзінің барлық мүмкін жағдайларының ішінде ең төменгі қалпында болады.

(Е) Жүктің бір ғана тепе теңдік қалпы болады, яғни жүктің тыныштықтағы қалпы нүктесінің орнымен және жіптің ұзындығымен толық сипатталады.

Тепе теңдік қалпының жалғыздығынан мына тұжырым шығыды:

(С) Жүк ілу нүктесінен жүргізілген перпендикулярдың бойында болады.

Шынында да, егер жүк осы вертикаль түзудің бойында болмаса, онда оны жүкпен қоса айналдыра бұрып, жаңа тепе теңдіктің қалпын аламыз.

1-сурет.

Осылайша талқылау барысында тәжірибеден алынған тағы бір тұжырымға сүйенеміз.

(S) Тепе теңдік қалыптағы денені немесе денелер жүйесін вертикаль түзуден айналдыра бұрғандағы дененің жаңа қалпы да тепе теңдік қалып болады.

(А) және (С) тұжырымдарынан мынаны айтуға болады:

(В) Ілу нүктесі - дан ілінген жүкке дейінгі қашықтық 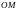жіптің ұзындығына тең болады (яғни қалыпты жағдайда жіп керіліп тұрады).

Осы тұжырымдарды пайдаланып, теореманы дәлелдейік. Центрі болатын шеңбер және онымен 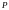нүктесінде жанасатын 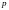түзуі берілсін

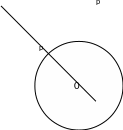
2-сурет

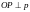болатынын дәлелдеу керек. Суретті вертикаль қабырғаға түзуі горизонталь, ал шеңбер одан жоғары орналасатындай етіп сызайық

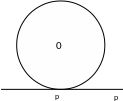
3-сурет

нүктесінің шеңбердің ең төменгі нүктесі екенін байқаймыз. Ұзындығы шеңбердің радиусына тең болатын жіп алып, бір ұшын нүктесіне бекітейік. Екінші ұшына жүк байлап, оны жіпке ілейік. ұшының нүктесімен беттесетінін көрсетеміз. Шынында да, біріншіден, (В) тұжырымы бойынша ұшы шеңбердің бойында болады, екіншіден, (А) тұжырымы бойынша жіптің бұл ұшы шеңбердің ең төменгі нүктесінде болады, яғни нүктесінде болады. Сонымен, жіп 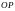радиусының бойында болады. (С) тұжырымы бойынша шеңбердің радиусы түзуіне перпендикуляр болады. Сонымен, теорема дәлелденді.

Осы талқыланған мысал өте қызықты және ол барлығымызға белгілі әрі қарапайым теореманы дәлелдеуге қолданылды. Бұл әдіс алдағы уақытта жаңа теоремаларды дәлелдеуде де қолданылады. Ол үшін математикалық теоремаларды дәлелдеуде механикалық әдістерді пайдалану дағдысын қалыптастыруымыз қажет. Жоғарыда келтірілген шеңберге жүргізілген жанама туралы теореманың дәлелдеуін эллипске жүргізілген жанама туралы теоремаға қолданамыз.

2. Эллипске жүргізілген жанама туралы есеп.

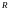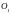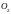Шеңбер деп берілген нүктесінен қашықтығы тұрақты санына тең болатын нүктелердің геометриялық орнын айтатынымыз белгілі. Осы анықтаманың жалпылауы эллипстің анықтамасы болады. Берілген және нүктелерінен қашықтықтарының қосындысы 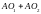тұрақты 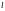санына тең болатын 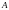нүктесінің геометриялық орнын эллипс деп атайды. және нүктелері эллипстің фокустары, ал саныны эллипстің үлкен осінің ұзындығы.

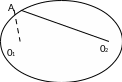
4-сурет

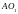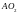Эллипстің кез келген нүктесін оның фокустарымен қосатын және кесінділері фокальдық радиустар деп аталады. Шеңбер және нүктелері беттесетін эллипстің дербес түрі болып табылады. Фокальдық радиустары да беттесіп, шеңбердің радиусына тең болады.

Әр бір оқушы эллипсті былайша сызуына болады: жіпті алып, оның ұштарын 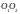қашықтығы жіптің ұзындығынан кем болатындай және нүктелеріне бекітеміз. Сонан соң жіпті кере отырып, қарындаштың ұшымен сызық сызамыз

5-сурет

Шеңбер сияқты, эллипспен ортақ тек бір ғана нүктесі болатын түзуді эллипске жанама деп атайды. Эллипске жанама туралы теореманы қарастырайық.

Теорема. Жанасу нүктесіне жүргізілген фокальдық радиустар жанамамен тең бұрыш жасайды.

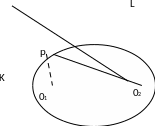
6-сурет

6 -суретт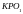е және 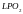бұрыштары тең.

Бұл теореманың дербес жағдайы шеңберге жүргізілген жанама туралы теорема болады. Шындығында да, шеңбер жағдайында екі фокальдық осьтер беттеседі, сондықтан шеңбер үшін эллипске жанама туралы теорема былайша тұжырымдалады: жанасу нүктесіне жүргізілген радиус жанамамен екі тең сыбайлас бұрыш жасайды. Ал бұл радиустың жанамаға перпендикуляр екенін көрсетеді.

Эллипске жанама туралы теореманы жоғарыдағы әдісті қолданып, яғни механикалық тәжірибе арқылы дәлелдейік. Вертикаль жазықтықта бірдей биіктікте және нүктелерін аламыз. Ұзындығы қашықтығынан артық болатын жіп алып, оның ұштарын және нүктелеріне бекітеміз. Жіптің бойымен еркін сырғанайтындай етіп, кішкене жүк тағамыз

7-сурет

Егер жүкті жіптің бойында еркін қозғалтсақ, онда ол өзінің тыныштық қалпы болып табылатын нүктесінде болады. Мынандай екі тұжырымның орындалатыны белгілі.

(С1) 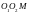жазықтығы вертикаль болады.

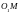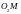(С2) нүктесі арқылы жазықтығындағы горизонталь түзумен және кесінділері бірдей бұрыш жасайды.

(С1) және (С2) тұжырымдарын жүктің қалыпты жағдайының жалғыздығынан да қортып шығаруға болады. Осы мақсатта кесіндісінің ортасы арқылы вертикаль түзу жүргізіп, жіпті ілінген жүкпен бірге 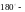қа бұрайық. Жіптің ұшы нүктесімен, ал ұшы нүктесімен беттеседі. (S) тұжырымына сәйкес жүктің қалыпты жағдайын аламыз, жіптің қалыпты жағдайының жалғыздығына байланысты жіп өзінің алғашқы жағдайында болады. үшбұрышы қа бұрғанда өзімен өзі беттесетіндіктен айналу өсі үшбұрыштың жазықтығында жатады. Яғни жазықтығы вертикаль ось арқылы өтеді. жазықтығының нүктесі арқылы өтетін вертикаль түзуді кез келген бұрышқа бұрғанда, ол өзі өзімен беттеседі, ал оның кесіндісімен жасайтын бұрышы кесіндісімен жасайтын бұрышпен беттеседі, яғни бұл бұрыштар тең.

Енді ілу нүктелері бірдей биіктікте болсын деген ұйғарымды алып тастайық. және кез келген нүктелер болсын. Оған бойымен емін еркін жүк қозғалатын жіп ілейік.

8-сурет

Тыныштық күйінде жүк нүктесінде болсын. Егер жүк нүктесінде болса және біз жіпті кез келген нүктесінен бекітсек, онда жүктің қалыпты жағдайы өзгермейді. Бұл жағдай бізге ілу нүктелері бірдей биіктікте болғанда жасалған тұжырымдарды жалпылауға мүмкіндік береді. Шындығында да, жіпті нүктесінің биіктігінде болатын 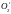нүктесінде бекітсек, нүктесінің қалпы өзгермейді. Сонда ілу нүктелері мен бірдей биіктікте болатын жағдайға келдік. Сондықтан, ілу нүктелері әртүрлі биіктікте болғанда да (С1) және (С2) тұжырымдарының дұрыс екенін көреміз. Сонымен қатар, (А) және (В) тұжырымдары да дұрыс болады.

Енді жанама туралы теореманы дәлелдейік. Фокустары және нүктелерінде, үлкен осінің ұзындығы болатын эллипс және 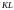түзуі оны нүктесінде жанасын (сурет 6). 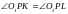болатынын дәлелдеу керек. Дәлелдеу үшін суреттің жазықтығы вертикаль, түзуі горизонталь, эллипс осы түзуінің жоғарғы жағында болатындай етіп суретті бұрамыз. Сонда эллипстің ең төменгі нүктесі болады. Ұзындығы болатын жіп алып, оған кішкене жүк іліп, жіптің ұштарын және нүктелеріне бекітейік. Сонан соң жүкті жібереміз. Ол қандайда бір нүктесінде болады. (С1) тұжырымына сәйкес нүктесі суреттің жазықтығында жатады. (В) тұжырымы бойынша ол эллипстің бойында болады. (А) тұжырым бойынша ол нүктесімен беттеседі. 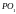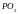Сонымен, жіп және кесінділерінің бойымен өтеді. (С2) тұжырымы бойынша осы кесінділердің түзуімен жасайтын бұрыштары бірдей.

Эллипске жүргізілген жанаманың фокальдық радиустармен бірдей бұрыш жасайтын қасиеті эллипске берілген нүкте арқылы жанаманы сызғыш пен циркульдің көмегімен салуға мүмкіндік береді. Ол үшін жанасу нүктесі , фокустары және арқылы түзулер жүргіземіз.

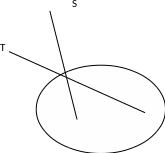
9-сурет

Сонан соң 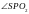немесе 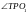бұрыштарының биссектрисасын жүргізу керек. Осы биссектриса эллипске жанама болады.