Методические указания к решению задачи № 5

Выполнение п.5-7 проводится с помощью программы МЕТПЕРЕМСЕРВИС.xls для электронной таблицы EXCEL по алгоритму, приведенному в [7, п.4.1.5]:

1. Система канонических уравнений метода перемещений

.

2. Матрица единичных реакций

.

3. Элементы вектора грузовых реакций определяются статическим способом (вырезанием узлов или частей основной системы).

4. Определение неизвестных перемещений

.

5. Вычисление вектора окончательной эпюры моментов

.

Все промежуточные матрицы показаны на экране в ячейках электронной таблицы.

Задача № 6

Расчет рамы на устойчивость методом перемещений

Для рамы, представленной на рис. 7, требуется:

1. Показать возможные формы потери устойчивости рассматриваемой рамы.

2. Определить критические значение силы для случаев, когда .

Рис.7

Исходные данные взять из табл. 8.

Таблица 8

Номер строки	Номер схемы	l, м		, кНм2
1	1	4	1	2000
2	2	6	2	3000
3	3	8	3	4000
4	4	4	4	5000
5	5	6	1	6000
6	6	8	2	2000
7	7	4	3	3000
8	8	6	4	4000
9	9	8	1	5000
0	0	4	2	6000
	е	а	б	в

Задача решается ручным способом и ПЭВМ.

Методические указания к выполнению задачи № 6

1. При расчете рамы методом перемещений для сжатых стоек нужно учитывать влияние продольных сил на величину реакций в связях основной системы метода перемещений с помощью трансцендентных функций , где (см. Приложение 1).

2. Программа расчета с помощью электронной таблицы EXCEL находится в УСТ.xls.

Задача № 7

Определение частот и форм собственных колебаний стержневой системы с конечным числом степеней свободы

Для рамы из двутавра с двумя сосредоточенными массами (рис. 8) требуется:

Рис.8

1. Определить сосредоточенные массы из условия, что каждая сосредоточенная масса в 10 раз больше массы участка рамы, где находится эта линия.

2. Определить число степеней свободы пронумеровать перемещения, определяющие положения масс при колебаниях (сформировать вектор перемещений ).

3. Записать систему дифференциальных уравнений свободных колебаний системы для вектора .

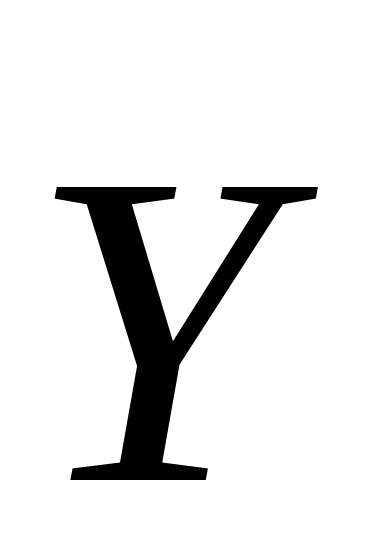4. Составить вековое уравнение для определения параметра собственных частот и форм колебаний.

5. С помощью программы СОБСТВЕК.xls для электронной таблицы EXCEL вычислить собственные частоты колебаний и показать изогнутый вид рамы, соответствующий каждой собственной форме. Проверить ортогональность полученных форм колебаний.

Исходные данные взять из табл. 9.

Таблица 9

Номер		l, м	Номер двутавра
строки	схемы
1	1	8	40
2	0	6	45
3	2	10	50
4	9	8	55
5	3	6	60
6	8	9	45
7	4	7	40
8	7	7	55
9	5	9	50
0	6	10	60
	а	б	в