1.4.2. Оптимизация сетевого графика по стоимости. Постановка задачи оптимизации. Методы оптимизации.

В данной курсовой работе будет рассмотрена задача минимизации стоимости проекта при фиксирован­ной его продолжительности. При оптимизации предполагают, что уменьшение продолжительности работы пропорционально ее стоимости. Под стоимостью выполнения работы подразумеваются лишь прямые затраты. При проведении оптимизации используются резервы времени некритических работ.

Задача моет иметь следующие варианты формулировки:

Задача 1

Пусть для каждой работы имеются следующие данные: d - минимальная продолжительность (срочный режим выполнения, экстренная продолжительность), которой соответствуют наиболь­шие затраты – C_max, и нормальная (наибольшая) продолжитель­ность — D, которой соответствуют наименьшие затраты - с_min . Предположим, что затраты на выполнение отдельных работ находятся в обратной зависимости от продолжительности их выполнения. Коэффициент h показывает, насколько увели­чится стоимость работы (i,j), при уменьшении ее продолжи­тельности на единицу времени:

(1.1)

Его называют коэффициентом дополнительных затрат (КДЗ). КДЗ для каждой работы равен тангенсу наклона угла аппроксимирующей прямой (рис 1.4 ).

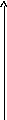
с

C_ijmax

c_ij

c_ijvin

d_ij t_ij D_ij t

Рис 1.4 Зависимость стоимости работы (i,j) от ее продолжительности

Необходимо свести к минимуму стоимость выполнения всего проекта, равную

,

так, чтобы время выполнения проекта не превысило заданного директивного срока Тд.

Задача 2

Для каждой работы известны: d — жесткое ограничение на продолжительность и нормальная продолжитель­ность D, а также зависимость стоимости работы от времени ее выполнения c(t). Необходимо свести к минимуму стоимость выполнения всего проекта, равную

,

так, чтобы время выполнения проекта не превысило заданного директивного срока Тд.

Задача 1 решается методами линейного программирования. Для решения задачи 2 возможно использовать различные методы в зависимости от вида целевой функции. Математическая модель задачи 2 имеет вид:

при ограничениях

T_j—T_i—t_ij≥0,

0≤d_ij≤t_ij≤D_ij, (1.2)

T₀=0,

Tкр=Тд.

Методы решения задачи 2 в зависимости от вида целевой функции показаны на рис 1.5.

вычислительные

методы теории графов

методы линейного программирования (симплекс-метод)

методы нелинейного программирования

методы динамического программирования

эвристические методы

Рис 1.5 Методы решения задачи 2

Рассмотрим частный случай задачи 2, когда целевая функция линейна, и предложим один из способов ее решения.

Постановка задачи

Пусть

c_ij— прямые затраты на выполнение работ, причем

c_ij= —a_ijt_ij+b_ij (a_ij≥0, b_ij>0),

где a_ij и b_ij— некоторые коэффициенты.

Продолжительность каждой работы задается в пределах

0≤d_ij≤t_ij≤D_ij, где

d_ij — жесткое ограничение;

D_ij — нормальное ограничение продолжительности работы.

Продолжительность критического пути, рассчитанная при d_ij=t_ij, будет наименьшим временем, за которое можно выполнить данный проект. Обозначим ее m.

Продолжительность критического пути, рассчитанная при t_ij=D_ij, будет наибольшим временем выполнения проекта. Обозначим ее M. Таким образом,

m≤Tкр≤M

Кроме того, задан директивный срок выполнения проекта Тд.

Задача: найти, насколько можно увеличить время выполнения отдельных работ, чтобы выполнить проект в заданный директивный срок с минимальными затратами, т.е. необходимо минимизировать целевую функцию вида

(1.3)

при ограничениях

T_j—T_i—t_ij≥0,

0≤d_ij≤t_ij≤D_ij,

T₀=0, (1.4)

Tкр==Тд, где  — параметр.

Очевидно, что для решения этой задачи можно применить симплекс-метод. В зависимости от частных особенностей графика возможно использование эвристических методов. Однако наиболее быстрым и экономичным решением будет решение на основе алгоритмов из теории графов. В разделе 1.5 рассмотрены именно такие алгоритмы.