3.4. Пример одноэтапной вероятностной модели управления запасом

Дневной спрос на продукцию в течение одного периода удовлетворяется мгновенно в начале периода. Спрос является случайной величиной, равномерно распределенной от 0 до 10 единиц. Стоимость хранения единицы продукции на протяжении периода равна 0,50 доллара, а штраф за дефицит единицы продукции – 4,50 доллара. Стоимость единицы продукции равна 0,50 доллара, стоимость размещения заказа – 25 долларов. Необходимо определить оптимальную стратегию заказа продукции.

РЕШЕНИЕ

По условию известны следующие параметры:

с=0,5 (доллара за единицу продукции)

p=4.5 (доллара за единицу продукции)

h=0.5 (доллара за единицу продукции за период)

K=25 (долларов)

Спрос является случайной величиной, равномерно распределенной от 0 до10 единиц.

Таким образом, рассчитаем критическое отношение:

Так как по условию известно, что спрос распределен равномерно, то можно рассчитать плотность вероятности:

Тогда получаем:

Найдем отсюда оптимальное значение объема запаса:

=0,8 , следовательно, y*=8.

Ожидаемое значение функции затрат определяется следующим образом:

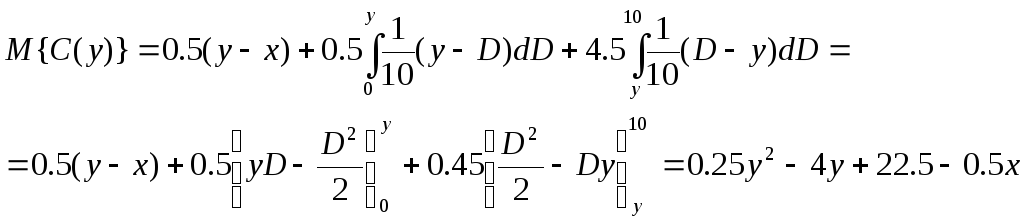
Наличный запас (х) нам известен, так как в условии об этом не сказано, то запас принимается равным нулю.

Величина sопределяется из уравнения:

Отсюда получаем:

Здесь вместо Sв правой части уравнения подставляется значение найденногоy*. Т.е. приS=8 это уравнение сводится к виду:

Решением данного уравнения является s=-2 илиs=18. Значениеs=18 (превышающее найденное ранееS) следует отбросить. Так как оставшееся значение является отрицательным, тоsне имеет допустимого значения. Следовательно, оптимальной стратегией является отказ от размещения заказа.

Вывод: заказывать не следует.

4. Реализация метода в среде delphi

4.1. Назначение программы

Разработанная программа предназначена для расчета одноэтапной вероятностной модели управления запасами при наличии затрат на оформление заказа. По умолчанию стоят данные, взятые из примера, рассматриваемого в разделе 3.4. Кроме того, оговорено, что спрос является случайной величиной, равномерно распределенной на интервале [a;b].

4.2. Расчет программы

Вводятся данные задачи. Необходимо определить оптимальный объем заказа. Это значение получаем исходя из формулы (2). Т.е. в данной программе:

Так как было оговорено, что распределение спроса является величиной равномерной, то плотность вероятности спроса за рассматриваемый период высчитывается по следующей формуле:

,

где aиb- нижняя и верхняя границы отрезка распределения.

Необходимо определить оптимальный объем заказа.

Таким образом, получаем:

Отсюда получаем выражение для нахождения оптимального объема заказа:

Ожидаемое значение функции затрат определяется из формулы (1)

Приведем данное выражение к квадратичному виду:

Обозначим в полученном выражении коэффициенты :

Таким образом, ожидаемое значение функции затрат будет выглядеть следующим образом:

Воспользуемся формулой (11) для нахождения величины s:

где y* - величина, найденная выше, как оптимальный объем заказа

Таким образом, преобразуем полученное уравнение для представления его в более удобной для расчета форме:

Для удобства расчета, обозначим полученные коэффициенты через:

, ,

Вычисляя полученное квадратное уравнение, получим корни s1 иs2, исходя из их численного значения, будем делать выводы (см. раздел 4.3).