1.5 Алгоритм решения задачи определения оптимальной величины партии в условиях скидки на размер заказа Двухуровневая система скидок.

Пусть величина заказываемой партии q может быть либо q<Q , либо q≥Q. При q<Q стоимость единицы продукции а1 , при q≥Q – а2 , причем а1>а2.

При q<Q имеем:

(1.3)

При q≥Q имеем:

(1.4)

Решая уравнения:

=0 и =0 (1.5)

находим:

(1.6)

(1.7)

Возможны случаи относительного размещения Q , ,и .Если <Q и ≥Q , то, учитывая , что а1>а2, выясним: , т.е. оптимальная партия≥Q .Если <Q и <Q , то для определения оптимальной партии необходимо сравнить и. Если<, то .Если ≥, то =Q .

Если же ≥Q и >Q , то .

Отсюда получаем следующий алгоритм:

1) Вычисляем . Если≥Q, то оптимальная партия заказа .

2) Если <Q ,то вычисляем и Δ=. Если Δ<0, то≤.Если Δ≥0, то =Q.

Трехуровневая система скидок.

Имеется три уровня цен: при q<Q1 цена а1; при Q1≤q<Q2 цена а2; при q≥Q2 цена а3. По условию а1>а2>а3; Q1, Q2 – размеры заказа, при достижении которых предоставляется скидка. Удельные издержки работы системы:

, i=1, 2, 3. (1.8)

Отсюда

(1.9)

Очевидно, что

(1.10)

Учитывая физическую реализуемость каждого локального экстремума, имеем следующий алгоритм:

1)Вычисляем . Если≥Q2 , то оптимальная партия заказа .

2)Если ≤Q2 , то вычисляем . Пусть Q2>≥ Q1 .Находим Δ=. Если Δ<0, то . Если Δ≥0, то .

3)Пусть ≤Q2 и < Q1 . Вычисляем . Легко показать, что< Q1 .Для определения оптимального размера заказа сравниваем с и .

1.6 Пример определения оптимальной величины партии в условиях двухуровневой системы скидок

Автомобильный завод заказывает отливки отливки металлургическому комбинату. Спрос на них 5000 штук в год. Комбинат выпускает различные типы отливок партиями. Стоимость переналадок – 500 рублей. Если заказ не превышает 2000 отливок, то стоимость каждой 40 рублей, если же заказ не меньше 2000, то – 32 рубля. Издержки содержания составляют 2% от стоимости единицы продукции. Определить оптимальную партию заказа.

Решение.

Имеем v=5000 штук в год; К=500 рублей; Q=2000 штук; а1=40 рублей за штуку; а2=32 рубля за штуку; р=2%.

Находим:

Так как >Q, то =2795 штук;

Общие издержки составят:

рублей в год.

1.7 Пример определения оптимальной величины партии в условиях двухуровневой системы скидок

Цех выпускает насосы. Издержки переналадки составляют 30 рублей. Потребность на насосы каждого вида постоянна и равна 600 штук в год. Себестоимость насоса зависит от величины заказа (табл.1.1).Издержки содержания – 2% от стоимости продукции. Установить оптимальную партию заказа.

Таблица 1.1

Величина заказа (штук)	Цена за штуку (рубли)
1 - 149	80
105 - 399	60
400 и более	40

Решение:

Имеем К=30 рублей; v=600 штук в год; Q1=150 штук; Q2=400 штук; а1=80, а2=60, а3=40 рублей за штуку; р=2%.

Находим

штук.

Так как =212<Q2=400, то вычисляем

штуки.

Имеем: 150<<400. Находим

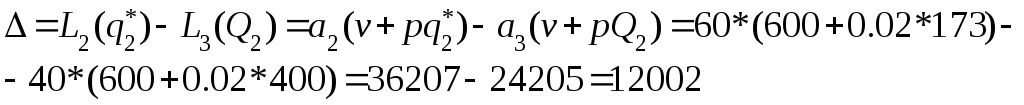
Так как Δ>0, следовательно, исходя из алгоритма, оптимальная партия заказа штукам.