3.7. Движение воды в реках

3.7.1. Распределение скоростей течения в речном потоке

В реках наблюдается турбулентный режим движения воды. Скорость течения потока подвержена тур­булентным пульсациям по величине и направлению, тем большим, чем больше скорость течения. Гидрометрические приборы для измерения скоростей течения измеряют только продольную составляющую скоро­сти, осредненную за некоторый интервал времени, примерно 100 секунд. Эти осредненные во времени скорости течения распре­делены в потоке неравномерно. Наибольшие скорости на­блюдаются на поверхности потока вдоль линии, соединяющей точки с наибольшей глубиной русла, наименьшие – у дна и берегов. Линия наибольших скоростей течения на поверхности потока называется динамической осью потока, или стрежнем.

Таким образом, типичная эпюра (графмк) распределении скоростей течения по глубине речного потока имеет максимум (u_max) на поверхности, минимум (u_min) не равный нулю,– у дна. Cскорость течения, близ­кая к средней на вертикали, располагается на глубине 0,6 h от поверхности (h – полная глубина потока на вертикали) (рис. 3.24, а). Среднюю скорость течения в поперечном сечении (v) рассчиты­вают по известным расходу воды (Q) и площади поперечного сечения (ω) по формуле Герона: .

Рис. 3.24. Вертикальное распределение скоростей течения в речном потоке [19]: а –типичное; б–под ледяным покровом; в–под слоем внутриводного льда (шуги); г–при попутном и встречном ветре; д– при влиянии растительности; е– при влиянии неровностей дна; 1 – ледяной покров; 2 – слой шуги; W – направление ветра; u_max – максимальная скорость течения; -и – обратное течение.

Однако, под влиянием ледяного покрова, ветра, растительности, неровностей рельефа дна и берегов это распределение скоростей нарушается (рис. 3.24 б – е).

3.7.2. Связь скорости течения в реках и каналах с характеристиками русла

Выделим в потоке столб воды высотой Н, равной глубине потока, и сечением 1 м². От угла наклона дна реки (канала) зависит величина составляющей силы тяжести, направленной параллельно водной поверхности. Пусть  – угол наклона дна по отношению к горизонтальной плоскости, а G – сила тяжести столба воды высотой Н и сечением 1 м² (рис.3.25).

Тогда искомая составляющая силы тяжести G_x («движущая» сила) равна G_x= Gsin, где sin= i – уклон дна. Из рис. 3.25 следует, что sin= G_x/G. Следовательно, движущая сила пропорциональна уклону G_x= Gi . Объем рассматриваемого столба воды равен произведению высоты (Н) на площадь сечения (1 м²), тогда его вес равен G=gН (g – ускорение силы тяжести, – плотность жидкости). Таким образом, G_x= Gi =gНi, т.е. движущая сила пропорциональна глубине потока и уклону. На рис. 3.25 сила G_x уравновешивается силой сопротивления Т. В курсах гидравлики показано, что сила сопротивления при турбулентном движении жидкости пропорциональна квадрату скорости течения, откуда следует широко известная в инженерной практике формула Шези для расчета скорости течения v:

(3.34)

где С – скоростной коэффициент, который определяется по формуле Маннинга

С =(Н^1/6)/n, (3.35)

n – коэффициент шероховатости, определяемый по таблицам в зависимости от состояния дна и стенок потока (ручей, река, канал, труба и др.).

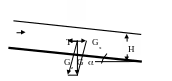
Рис. 3.25. Силы, действующие при движении столба воды высотой Н (обозначения в тексте).

Коэффициент шероховатости речного русла n находят по спе­циальным таблицам. Например, для ровных незаросших русел с песчаным дном n = 0,020 – 0,023; для извилистых русел с неров­ным дном n = 0,023-0,033; для пойм, заросших кустарником, n = 0,043-0,55 и т.д.

Согласно формуле Шези, скорость течения в речном потоке тем больше, чем больше глубина русла и уклон водной поверхности и меньше шероховатость русла. При заданном расходе воды, увеличение шероховатости русла в результате образования ледяного покрова или зарастания дна и берегов водной рас­тительностью, приводит к увеличению глубины (и повыше­нию уровня воды). Следовательно, зимой на реках, покрытых льдом, уро­вень воды обычно выше, чем летом при тех же расходах воды. В условиях теплого климата в период бурного развития растительности в руслах рек уровень воды также повышается.