1.2. Третья функция сложного процента
Эта
функция, являясь обратной ко второй,
определяет размер вносимой вначале
каждого промежутка времени суммы
с целью получения в конце периода
итоговой суммы размера
при определенном проценте
Исходной здесь является вторая функция сложного процента (1.6). Из нее можно найти
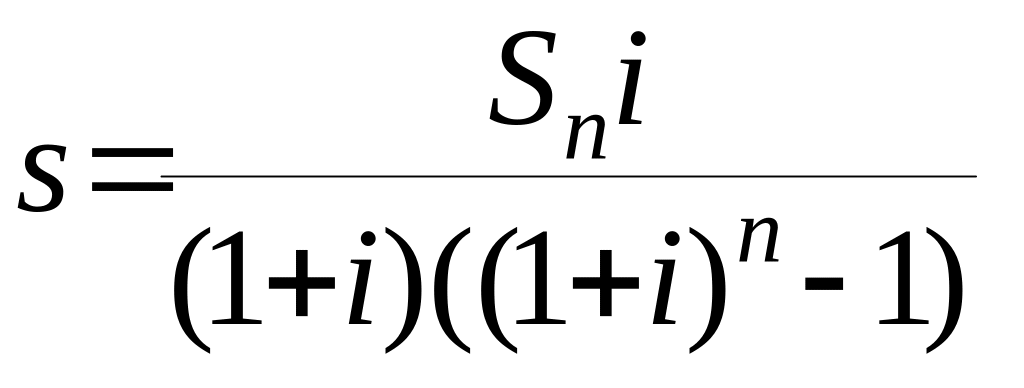(1.10)
Сумма называется авансовой суммой фонда возмещения, а величина
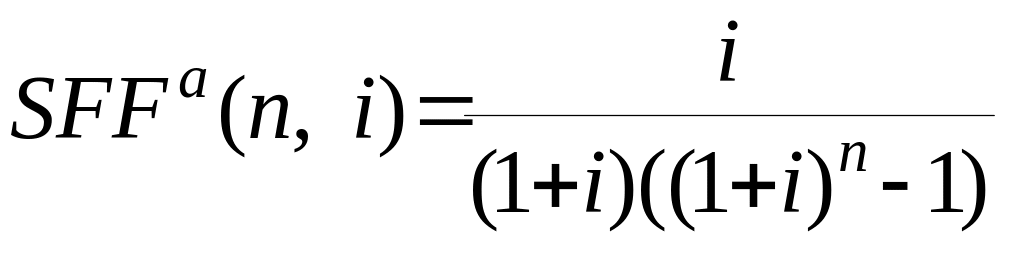(1.11)
авансовым фактором фонда возмещения.
Пример
1.2. Необходимо
в течение 10 лет накопить сумму в размере
150000 у.е. для приобретения земельного
участка с гостиницей. Какую сумму
необходимо депонировать в начале каждого
года при годовом проценте
Решение: На основании (1.10)
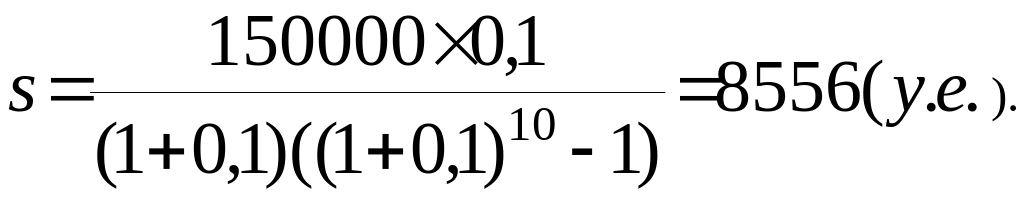
Если в качестве исходной функции брать (1.8), то на ее основе третья функция будет определена так
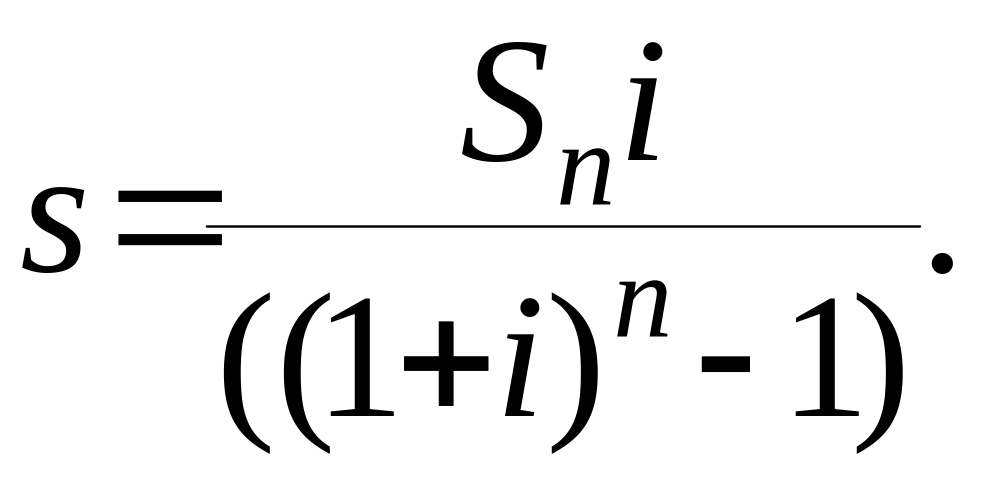(1.12)
Ее называют обычной суммой фонда возмещения, а величину
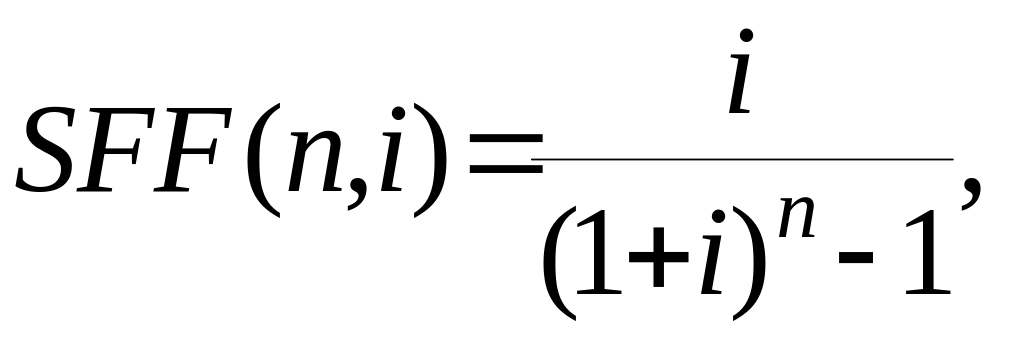(1.13)
обычным фактором фонда возмещения.
1.3. Четвертая и пятая функции сложного процента
Четвертая
функция сложного процента определяет
текущую стоимость будущей единицы. Эта
функция является обратной к первой и
ее еще называют функцией дисконтирования
(от английского discount
– скидка, сбавка). Суть ее заключается
в следующем. Если через
промежутков времени при ставке процента,
равной
стоимость объекта составит
то его текущая стоимость, исходя из
(1.1) будет
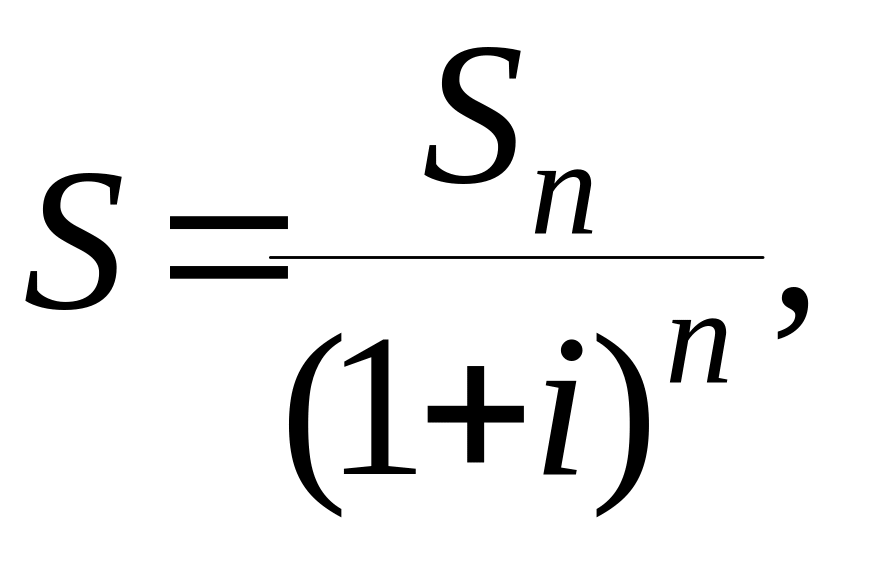(1.14)
т.е.
произойдет скидка стоимости
в
раз.
Сумму
(1.14) называют текущей
стоимостью накопленной в будущем суммы
а функцию
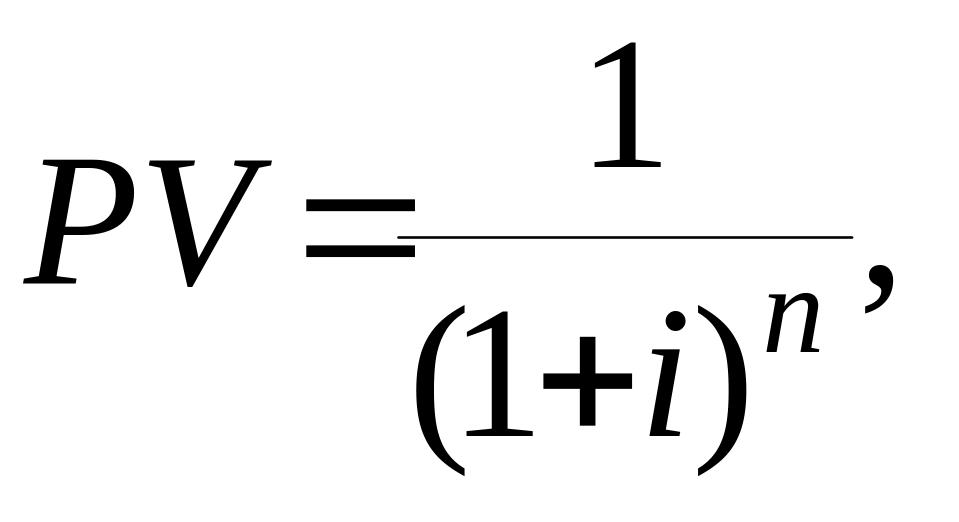(1.15)
фактором текущей стоимости будущей единицы.
Пример 1.3 [4]. Земельный спекулянт полагает, что может через 4 года продать застройщику земельный массив площадью 100 га по цене 10000 у.е. за 1 га. Какая цена, оплаченная сегодня, позволит спекулянту получить накапливаемый ежегодный доход 12%.
Решение:
В данном случае
для 1 га
Тогда на основании (1.14) S
= 6355,18 у.е. для 1 га, а для 100 га S
= 635518 у.е., т.е. спекулянту остается лишь
обмануть продавца и заплатить ему только
635518 у.е., твердо зная, что через 4 года он
продаст данный земельный участок за 1
млн. у.е.
Пятая функция сложного процента определяет текущую стоимость накопленной единицы. Ее еще называют текущей стоимостью аннуитета.
Такая функция является комбинацией второй и четвертой. В соответствии со второй функцией определяется будущая стоимость аннуитета, а в соответствии с третьей – его текущая стоимость.
Суть
этой функции в следующем. Согласно
авансовому аннуитету на счет в начале
каждого из
промежутков поступает сумма
с выплатой процента
в конце каждого из них. Таким временных
промежутков
Накопленная сумма составит величину
(1.6). А в соответствии с (1.14) находится
текущая
стоимость авансового аннуитета.
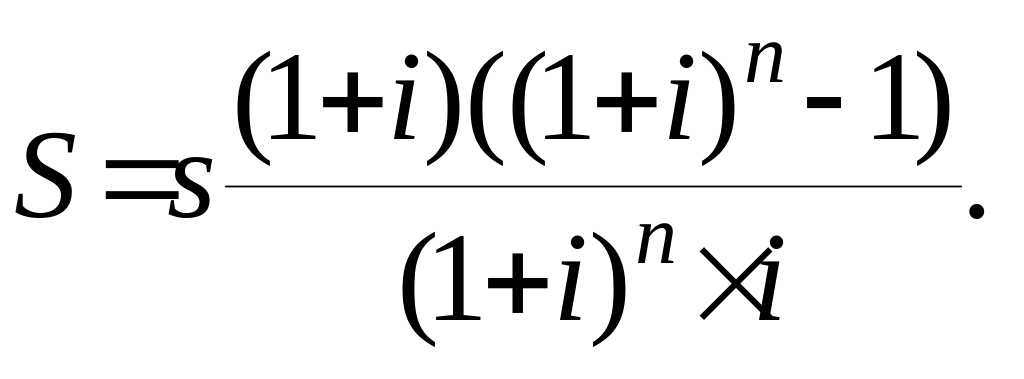(1.16)
Если рассматривать обычное накопление, то подстановка (1.8) в (1.14) приводит к функции
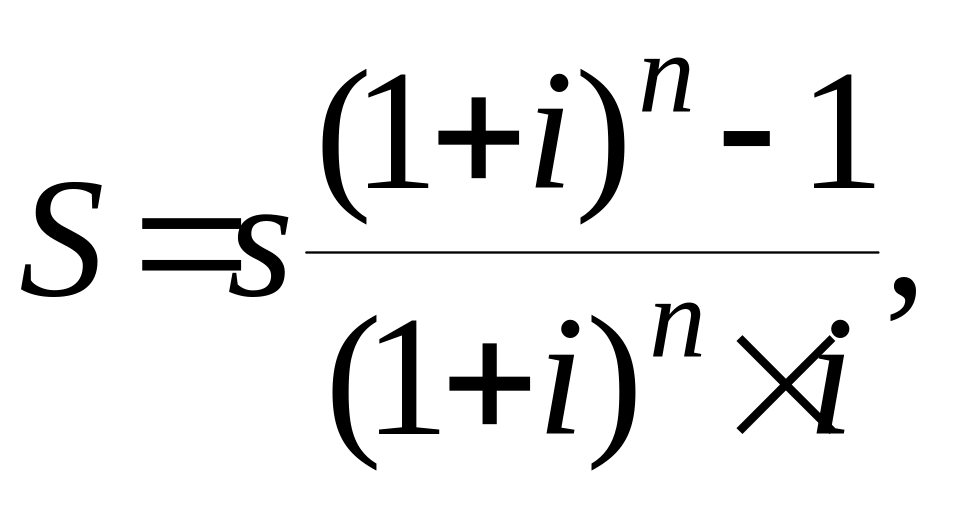(1.17)
называемой текущей стоимостью обычного аннуитета.
Соответственно функции
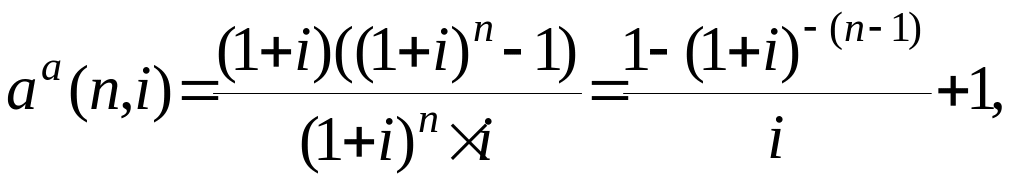(1.18)
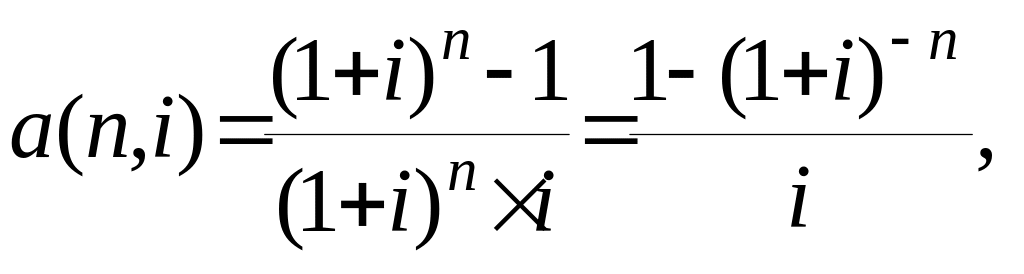(1.19)
называются факторами текущей стоимости авансового (1.18) и обычного (1.19) аннуитетов.
Пример
1.4. Земельный
участок сдается в аренду за 200 у.е. в
месяц, поступаемых авансом. Ежемесячно
начисляется процент в размере
Срок
аренды 2 года, т.е. 24 месяца. Оценить
текущую стоимость такой аренды.
Решение:
В данном примере
Тогда в соответствии с (1.16) будет
Рассмотрим некоторые варианты решения данного примера:
а)
Если платеж при тех же условиях
осуществляется в конце месяца, то в
соответствии с (1.17) стоимость аренды
будет
б)
Если платеж поступает в начале каждого
года, а процент начисляется лишь в конце
года, то тогда
и в соответствии с (1.16) стоимость аренды
составит
в)
При платеже
в конце каждого года при
в соответствии с (1.17) стоимость аренды
составит
г)
При внесении всей платы
в
конце срока аренды ее текущая стоимость
при годовой процентной ставке
будет
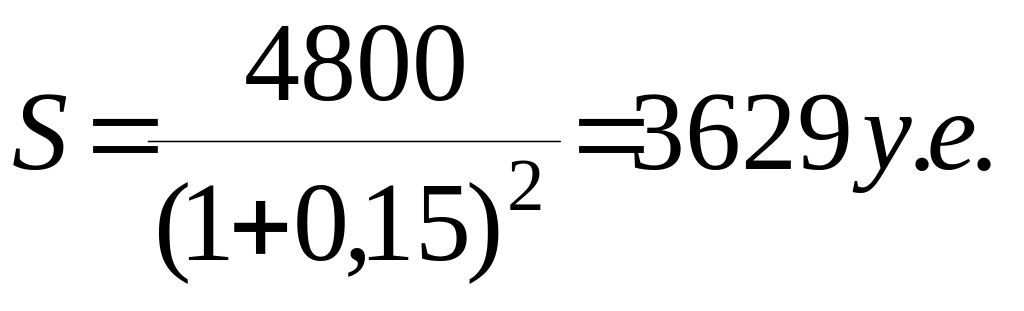
Исходя из примера 1.4 можно заключить, что пятая функция сложного процента позволяет выработать различные варианты аренды по ее текущей стоимости.