Шпоры и задачи 2012 (Саломатин) [7171 вопросов] / scr / doc / 11

11. Циклический и диадный сдвиги, циклическая и диадная свертки: определение, методы представления и вычислений

Циклическая свертка периодических последовательностей длины N определяется выражением

При этом справедливы следующие соотношения: x[-n]=x[N-n] и h[-n]=h[N-n].

В матричном виде циклическая свертка записывается следующим образом:

Например для ,

Согласно теореме о свертке, циклическая свертка может быть вычислена через дискретные преобразования Фурье:

где , - Фурье-образы соответственно последовательностей и .

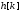Рассмотрим функцию S(x) дискретной переменной x , принимающей значение в интервале 0,1,2…N-1. Функция S(x⊕τ) называется диадным сдвигом функции S(x). Сущность диадного сдвига заключается в перестановке отсчетов исходной функции. В частности, на место x становится отсчет форм x⊕τ.

Пример: S(x) = [0 0 1 1 1 1 0 0 ]. Осуществим диадный сдвиг , т.е. S(x⊕τ) при τ =4, τ − величина диадного сдвига. Пронумеруем все выборки исходного сигнала двоичными числами 0,1,2…N-1: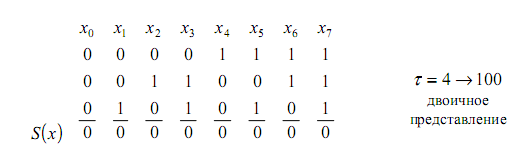

Произведем диадный сдвиг выборок сигнала

x0⊕τ= 000⊕100=100→x4

x1⊕τ= 001⊕100=101→x5

x2⊕τ= 010⊕100=110→x6

x3⊕τ= 011⊕100=111→x7

x4⊕τ= 100⊕100=000→x0

x5⊕τ= 101⊕100=001→x1

x6⊕τ= 110⊕100=010→x2

x7⊕τ= 111⊕100=011→x3

Это эквивалентно следующей перестановке отсчетов сигнала:

Понятие диадного сдвига позволяет обобщить понятие свертки и корреляционной функции. Так как суммирование и вычитание по модулю два совпадают, то диадная свертка совпадает с диадной корреляцией и определяется следующим выражением:

Можно доказать, что

1.Спектр функции S(x) инвариантен относительно диадного сдвига аргумента.

2. Свертка временных последовательностей равна преобразованию Уолша-Адамара от произведения спектров сворачиваемых последовательностей (теорема о свертке). Отсюда следует, что корреляционная функция может быть вычислена при помощи двойного преобразования Уолша-Адамара: