
- •25.Циклическая свертка: определение, методы представления и вычислений
- •Дискретное преобразование Лапласа и z-преобразование: свойства z-преобразования
- •Методы спектрального анализа нестационарных дискретных сигналов
- •Периодограммная оценка спм.
- •Коррелограммный метод оценки спм.
- •28. Дискретные экспоненциальные функции
- •29. Модели анализатора спектра.
- •30. Дискретное преобразование Фурье
- •Свойства дпф
28. Дискретные экспоненциальные функции
В дискретных преобразованиях Фурье используется система дискретных экспоненциальных функций (ДЭФ), определяемых как

Переменные k и n принимают целочисленные значения (0,1,…,N-1). Переменную k отождествляют с номером функции, а переменную n – с номером отсчета.
Если
обозначить
 ,
тогда
,
тогда .
Функция
.
Функция носит названиеповорачивающий
множитель.
носит названиеповорачивающий
множитель.
Образуем матрицу
 ,
,
строки
которой нумеруются переменной k,
столбцы переменной n,
а на пересечении k-й
строки и n-го
столбца записана величина
 .
.
Прямое и обратное ДПФ имеет следующую матричную форму записи:
 ;
;
 ,
,
где
 -
вектор отсчетов сигнала,
-
вектор отсчетов сигнала, -
вектор коэффициентов спектра ДПФ;T
– оператор транспонирования .
-
вектор коэффициентов спектра ДПФ;T
– оператор транспонирования .
Заметим, что для поворачивающего множителя справедливы следующие соотношения:
 и,
следовательно,
и,
следовательно,
 ,
т.е. поворачивающий множитель первой
степени является корнемN-й
степени из единицы;
,
т.е. поворачивающий множитель первой
степени является корнемN-й
степени из единицы; ;
;
 .
.
Для любого N матрица FN обладает следующими свойствами:
Матрица FN ортогональна и унитарна:
 ;IN-
единичная диагональная матрица.
;IN-
единичная диагональная матрица.Матрица FN- симметрична:
 .
.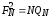 ,
где QN-
симметричная
матрица перестановок
,
где QN-
симметричная
матрица перестановок

 .
.Сопряженная матрица имеет вид
 .
.Обратная матрица имеет вид
 .
.
Для
формирования обратной матрицы необходимо
прочесть в обратном порядке элементы
 с
отличными от нуля степенями (kn
0)
строк матрицы FN
.
с
отличными от нуля степенями (kn
0)
строк матрицы FN
.
Мультипликативность
 ;
; .
.
При умножении любых двух строк (столбцов) матрицы ДЭФ получается строка (столбец) той же матрицы. Номер строки (столбца) равен сумме номеров сомножителей.
Факторизуемость. Для любого N, разложимого в произведение отличных от 1 чисел N1 и N2, матрица функций ДЭФ порядка N представима в виде

или в виде
 ,
,
где
 и
и -
матрицы перестановок, отвечающие
транспонированию прямоугольных матриц
соответственно размеров (N1N2)
и (N2N1);
-
матрицы перестановок, отвечающие
транспонированию прямоугольных матриц
соответственно размеров (N1N2)
и (N2N1);
 -
диагональная матрица, образованная
последовательностью поворачивающих
множителей
-
диагональная матрица, образованная
последовательностью поворачивающих
множителей

29. Модели анализатора спектра.
Обработка сигналов, связанная с анализом их спектров, называется спектральным анализатором. Спектральный анализ используется во многих алгоритмах ЦОС, в частности, при распознавании, обнаружении и сжатии сигналов. Матем. основой спектр.анализа явл-ся ДПФ.
Структурная схема для спектра-анализатора: N-точечное ДПФ

Анализатор спектра в виде гребёнки фильтров:

Гребёнка фильтров:
выдаёт N спектральных отсчётов в каждый момент времени;
требует N операций умножения- накопления на 1 отсчёт сигнала.
30. Дискретное преобразование Фурье
Дискретное преобразование Фурье устанавливает связь между временным и частотным представлениями сигнала при разложении его по гармоническим дискретно-экспоненциальным функциям.
Дискретные прямое и обратное преобразования Фурье
 ,
k=0,…,N-1
(33)
,
k=0,…,N-1
(33)
и
 ,
n=0,…,N-1
(34)
,
n=0,…,N-1
(34)
где {x[n]}- последовательность отсчетов сигнала
{X(k)} – последовательность спектральных коэффициентов
Свойства дпф
Цикличность. Последовательность коэффициентов ДПФ является периодической последовательностью
 .
.
Последовательность отсчетов сигнала, полученная обратным ДПФ (ОДПФ) из ее коэффициентов также периодична
 .
.
Это
свойство следует из периодичности ядра
преобразования
 .
.
Симметрия.
 ;
;
 ;
;
 .
.
Теорема сдвига (инвариантность относительно сдвига во времени и частоте).
Пусть
 - последовательность, образованная из
последовательности
- последовательность, образованная из
последовательности циклическим сдвигом на
циклическим сдвигом на отсчетов.
Тогда справедливо соотношение
отсчетов.
Тогда справедливо соотношение
 .
.
Свойство показывает, что при сдвиге по времени амплитудный спектр не меняется. Изменяются только фазы гармонических составляющих.
Аналогичное свойство для частотной области
 .
.
Интерполяция. Спектр последовательности, полученный раздвиганием и дополнением нулями элементов некоторой исходной последовательности, образуется с помощью интерполяции отсчетов ДПФ исходной последовательности.
Четные компоненты спектра удлиненной последовательности совпадают с аналогичными значениями спектра исходной последовательности. Нечетные компоненты спектра удлиненной последовательности можно рассматривать как результат интерполяции.
Теорема отсчетов. Периодическое M кратное повторение исходной последовательности приводит к увеличению в M раз значений спектральных компонент её ДПФ, размещению их с шагом M и дополнением остальных позиций спектра нулями:
 ,
,
где
 -
символ Кронекера.
-
символ Кронекера.
Децимация. Пусть {XNM(k)} - множество коэффициентов спектра ДПФ последовательности {x[n]; n=0,1,…,NM-1}:
 ,
,
m = 0,1,…,M-1; n = 0,1,…,N-1
Отсюда можно получить выражение для спектра децимированной последовательности
 .
(46)
.
(46)
Теорема о перестановках. Если P не имеет общих делителей с N, то
 ,
(47)
,
(47)
где
 .
Эта теорема является аналогом теоремы
о масштабах интегрального преобразования
Фурье. Но если изменение масштаба
сигнала, например, растяжение сигнала
по координате вP
раз, приводит к сжатию его спектра Фурье
в P
раз, то для дискретных последовательностей
и их ДПФ это соответствует перестановкам
элементов последовательностей.
.
Эта теорема является аналогом теоремы
о масштабах интегрального преобразования
Фурье. Но если изменение масштаба
сигнала, например, растяжение сигнала
по координате вP
раз, приводит к сжатию его спектра Фурье
в P
раз, то для дискретных последовательностей
и их ДПФ это соответствует перестановкам
элементов последовательностей.
Линейность. Пусть даны две последовательности
 и
и ,
для которых ДПФ равны соответственно
,
для которых ДПФ равны соответственно и
и .
Спектр взвешенной суммы последовательностейa
.
Спектр взвешенной суммы последовательностейa + b
+ b =
= равен аналогичной взвешенной сумме
спектров:
равен аналогичной взвешенной сумме
спектров:
 =
a
=
a + b
+ b .
(48)
.
(48)
Теорема о свертке. Спектр свертки двух последовательностей
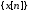 и
и равен
произведению спектров
равен
произведению спектров и
и сворачиваемых последовательностей:
сворачиваемых последовательностей:
 .
(49)
.
(49)
Теорема позволяет вычислить циклическую свертку y[l] при помощи ДПФ по формуле
{y[l]} = ДПФ-1(ДПФ{x[n]} ДПФ{h[n]}).
ДПФ вещественной последовательности. Пусть {x[n]} – вещественная последовательность. ДПФ такой последовательности имеет следующие особенности:
Спектральные коэффициенты комплексно сопряжены относительно N/2
 ,
,
где
оператор означает
комплексное сопряжение.
означает
комплексное сопряжение.
Если x[n] – четная последовательность, т.е. x[n]=x[-n], то спектр ДПФ {X(k)} также представляет собой вещественную последовательность.
Если x[n] – нечетная последовательность, т.е. x[n]=-x[-n], то {X(k)} представляет собой чисто мнимую последовательность.
Данное свойство позволяет при помощи одного преобразования вычислить ДПФ двух действительных последовательностей, либо использовать N/2 –точечное преобразование для вычисления спектра N точечной последовательности.
