
- •25.Циклическая свертка: определение, методы представления и вычислений
- •Дискретное преобразование Лапласа и z-преобразование: свойства z-преобразования
- •Методы спектрального анализа нестационарных дискретных сигналов
- •Периодограммная оценка спм.
- •Коррелограммный метод оценки спм.
- •28. Дискретные экспоненциальные функции
- •29. Модели анализатора спектра.
- •30. Дискретное преобразование Фурье
- •Свойства дпф
25.Циклическая свертка: определение, методы представления и вычислений
Свёртка - базовая операция в ЦОС. В процессе кодирования- декодирования сигналов с использованием конечных полей приходится неоднократно вычислять произведение двух векторов(полиномов), которое принято называть свёрткой.
Понятие круговой свёртки используется только для периодических последовательностей.
Циклическая свертка периодических последовательностей длины N
определяется выражением (1):

При этом справедливы следующие соотношения: x[-n]=x[N-n] и h[-n]=h[N-n].
В матричном виде циклическая свертка записывается следующим образом:
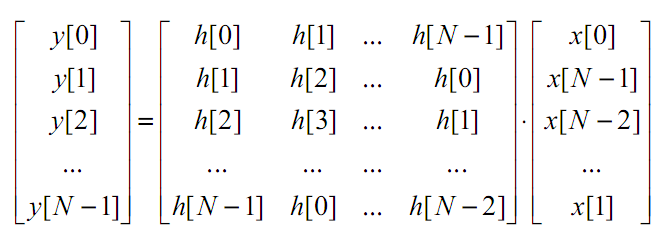
Найдём ДПФ круговой свёртки Y(k), если ДПФ посл-тей x1(nT) и x2(nT) соответственно равны X1(k) и X2(k):

Заметим,что периодическая посл-ть x3(nT), равная произведению периодических посл-тей x1(nT) и x2(nT) имеет ДПФ:

Циклическую свертку можно вычислить
с использованием ДПФ по след.алгоритму:
Вычислить ДПФ X1(k) и X2(k) для посл-тей x1(nT) и x2(nT)
Вычислить ДПФ Y(k) для свёртки y(nT)
Вычислить у(nT) путём вычисления ОДПФ по найденному Y(k)
с использованием преобразования Уолша-Адамара
с использованием ТЧП
Дискретное преобразование Лапласа и z-преобразование: свойства z-преобразования
Дискретным преобразованием Лапласа называется след.ряд:

где
 -
символическое обозначение дискретного
преобр-я Лапласа;
-
символическое обозначение дискретного
преобр-я Лапласа;
 -
оригинал- вещественная или комплексная
посл-ть, для которой выполняется условие
-
оригинал- вещественная или комплексная
посл-ть, для которой выполняется условие
 ;
;
 -
D-изображение
посл-ти
-
D-изображение
посл-ти
 ,результат
дискретного преобр-я Лапласа.
,результат
дискретного преобр-я Лапласа.
Дискретное
преобр-е Лапласа однозначно связывает
посл-ть
 с
её D-изображением
с
её D-изображением
 и справедливо только в области абсолютной
сходимости ряда
и справедливо только в области абсолютной
сходимости ряда

определяемой
абсциссой сходимости
 .
На
комплексной p-
плоскости это область, где
.
На
комплексной p-
плоскости это область, где
 .
.
При исследовании дискретных сигналов и линейных систем, как правило, вместо преобр-я Лапласа используют Z- преобразование, которое получается из дискретного преобр-я Лапласа в результате замены переменных
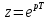 ,
,
где
p-
оператор Лапласа: p=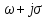
Комплексная переменная z может быть представлена в двух формах:
в алгебраической z=c+jd
в показательной z=r·ejφ,
где радиус r является модулем, а угол φ- аргументом переменной z
Z-
преобр-ем посл-ти
 называется
след.ряд:
называется
след.ряд:

где
 -
символическое обозначениеZ-преобр-я;
-
символическое обозначениеZ-преобр-я;
 -
оригинал- вещественная или комплексная
посл-ть, для которой выполняется условие
-
оригинал- вещественная или комплексная
посл-ть, для которой выполняется условие
 ;
;
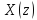 -
D-изображение
посл-ти
-
D-изображение
посл-ти
 ,результатZ-
преобр-я.
,результатZ-
преобр-я.
Z-
преобр-е однозначно связывает посл-ть
 с
её z-
изображением
с
её z-
изображением
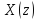 и
справедливо только в области абсолютной
сходимости ряда
и
справедливо только в области абсолютной
сходимости ряда

Основные свойства z-преобразования
Одним из важнейших св-в Z- преобразования является св-во его единственности, в соответствии с которым посл-ть x(nT) однозначно определяется z-изображением X(z) в области его сходимости и наоборот, z- изображение X(z) однозначно определяет посл-ть x(nT).
Линейность
Если
посл-ть
 равна линейной комбинации посл-тей
равна линейной комбинации посл-тей
 ,
,
то её z- изображение равно линейной комбинации z- изображений данных посл-тей:

Z-преобразование задержанной посл-ти (теорема о задержке).
Z- преобр-е посл-ти x[(n-m)T], задержанной на m (m>0) отсчётов, равно z- изображению незадержанной посл-ти x(nT), умноженному на z-m:
 ;
;
Z
Z- преобразование свёртки посл-тей (теорема о свёртке).
Свёрткой
посл-тей
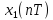 и
и называется посл-ть
называется посл-ть ,
определяемая соотношением
,
определяемая соотношением

Z- изображение свёртки равно произведению z- изображений свёртываемых посл-тей

