1.5. Определение необходимого количества наблюдений для достижения требуемой точности

Минимальная абсолютная погрешность определяется по формуле

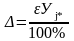, (1.8)

где ε – относительная погрешность, ε = 10 %;

* - среднее значение выходного параметра в j*-ом опыте, для которого дисперсия Sj* максимальна, см. таблицу 1.2.

;

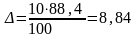Необходимое число наблюдений определяется из условия

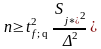, (1.9)

где n – первоначальное количество наблюдений, n = 9;

t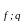 - критерий Стьюдента для уровня значимости q = 0,05 и числа степеней свободы f = n – 1 , f = 9 – 1.

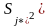- дисперсия в j-ом опыте;

∆ - минимальная абсолютная погрешность.

9 ≥ 2,31² · 55,44 / 8,84² =3,78

Условие выполняется, поэтому число наблюдений является достаточным

1.6. Оценка однородности дисперсии

Оценить однородность дисперсии можно оценить при помощи следующей формулы

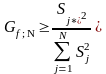, (1.10)

где S²j* - дисперсия в j*-ом опыте, т.е. максимальная дисперсия;

S²j - дисперсия в j-ом опыте;

Критерий Кохрена G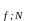 для уровня значимости q = 0,05, число степеней свободы f = 8, определяется из таблицы 4 приложения [1]

0,52 ≥ 88,4/ (55,44+ 14,1 + 119,7 + 56,2) = 0,36

Так как условие выполняется, то значит, дисперсии однородны

1.7. Определение обобщённой дисперсии

S² = (1/N)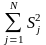 , (1.11)

где N – число опытов;

S²j – дисперсия j-го опыта.

S² = (1/4) *(55,44+ 14,1 + 119,7 + 56,2) = 61,36

1.8. Определение коэффициентов регрессионного уравнения

Используя матрицу плана ПФЭ и значения результатов опытов j можно построить уравнение регрессии для двухфакторного ПФЭ вида

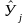= bo + b1x1 + b2x2 , (1.12)

где bо, b1, b2 - коэффициенты регрессии;

x1, x2 - рассматриваемые факторы.

Для этого необходимо рассчитать значения коэффициентов по формуле

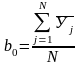, (1.13)

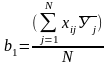, (1.14)

где N – число опытов;

j – номер опыта;

i – номер фактора;

xij – значение i-го фактора в j-ом опыте в кодированном виде;

- значение результата опыта.

bo = (88,4+62,68+84,64+63,12) / 4 = 74,7

b1 = (88,4-62,68+84,64-63,12) / 4 = 11,8

b2 = (88,4+62,68-84,64-63,12) / 4 = 0,83

1.9. Оценка значимости членов регрессионного управления

Значимость членов регрессионного уравнения оценивается по условию

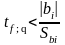, (1.15)

где t - критерий Стьюдента, табл. 1 приложения [1] t = 2,036;

bi - i-ый коэффициент регрессионного уравнения;

S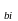 - дисперсия коэффициентов.

Обобщённая дисперсия коэффициентов определяется по формуле

S = 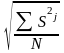, (1.16)

где S² - обобщённая дисперсия;

N – число опытов;

n – число наблюдений в опыте.

S = 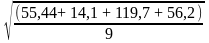= 7,83

Для коэффициента b0 = 74,7

2,036 < 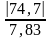= 9,54

Для коэффициента b1 = 11,8

2,036<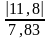 = 1,5

Для коэффициента b2 = 0,83

2,036 <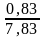 = 0,1

Для коэффициента b0 условие (1.15) выполняется, это означает что b0, входит в уравнение регрессии, а для коэффициентов b1, b2 условие (1.15) не выполняется. Следовательно, уравнение регрессии примет вид:

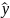= 74,7 +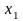 + 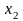(1.17) 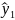=74,7+(115-110/5)+(35-30/5)=76,7

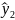=74,7+(105-110/5)+(35-30/5)=74,7

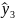=74,7+(115-110/5)+(25-30/5)=74,7

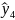=74,7+(105-110/5)+(25-30/5)=72,7