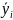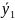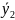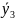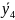Министерство образования и науки Российской Федерации

Санкт-Петербургская государственная лесотехническая академия

им. С.М.Кирова

Кафедра технологии деревообрабатывающих производств

КУРСОВАЯ РАБОТА

на тему: «Исследование формирования лакокрасочного покрытия

древесины на лаконаливной машине»

по дисциплине: «Основы научных исследований»

Выполнила студентка

специальность 250403

3 курс МТД з/о 1 группа

№ зачётной книжки 08129

Колосова И.И.

Руководитель курсовой работы Кузнецова Е.Г.

Санкт – Петербург

2011

Содержание

Введение 3

Задание 4

1 МЕТОДИКА ПРОВЕДЕНИЯ РАБОТЫ И СООТВЕТСТВУЮЩИЕ

РАСЧЁТЫ 5

1.1 Определение основных уровней факторов и интервалов варьирования 5

1.2. Перевод нижних и верхних значений уровней каждого фактора в кодированный вид 6

1.3. Построение плана ПФЭ и проведение имитационного эксперимента 7

1.4. Обработка результатов наблюдений для каждого опыта 9

1.5. Определение необходимого количества наблюдений для достижения требуемой точности 10

1.6. Оценка однородности дисперсии 11

1.7. Определение обобщённой дисперсии 11

1.8. Нахождение коэффициентов регрессионного уравнения 11

1.9. Оценка значимости членов регрессионного управления 12

1.10. Проверка адекватности регрессионного уравнения 13

1.11. Перевод регрессионного уравнения из кодированного вида в натуральный 15

Вывод 15

Литература16

Введение

При проведении научных исследований в области деревообработки широко используются методы однофакторного и многофакторного экспериментов. По методу однофакторного эксперимента последовательно изучается влияние на процесс каждого из принятых переменными факторов. Методика многофакторного эксперимента позволяет изучать процесс при изменении в каждом последующем опыте одновременно нескольких переменных факторов. Достоинством метода многофакторного эксперимента в сравнении с однофакторным являются: значительное сокращение числа опытов для решения задач исследования, возможность построения по результатам исследования уравнения регрессии – математико-статической модели изучаемого процесса, позволяющей исследовать, оптимизировать процесс и управлять им. При этом процесс исследуется и управляется в условиях воздействия на него факторов в их взаимосвязи.

Одним из таких методов является метод полного факторного эксперимента (ПФЭ), который применяется на первом этапе исследования процессов. С его помощью удается при небольших затратах времени и средств получить информацию об изучаемом процессе, хотя и не всегда полную.

Целью выполнения курсовой работы на тему: «Исследование процесса деревообработки методом полного факторного эксперимента» является овладение методикой планирования ПФЭ, обработки и анализа его результатов.

Сущность метода полного факторного эксперимента.

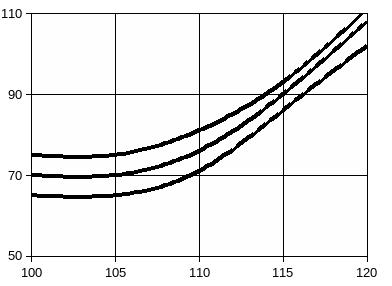
Метод полного факторного эксперимента (ПФЭ) применяется для решения описательных задач научного исследования, которые формулируются так: установить влияние на выходной параметр исследуемого процесса ряда переменных факторов. При этом предполагается, что исследуемый процесс можно описать линейным уравнением регрессии, связывающим выходной параметр процесса ŷ и влияющие на процесс переменные факторы х_i . Такое уравнение – полином первой степени – в общем имеет следующий вид:

ŷ = b₀+b₁x₁+b₂x₂+…+b_ix_i

где b₀ – свободный член;b_1,b_2,…,b_i –линейные коэффициенты регрессии;i- номер фактора, i=1,2,…,к.

Для построения уравнения регрессии по результатам ПФЭ достаточно провести опыты при варьировании факторов только на двух уровнях – на НУ и ВУ. При этом опыты должны быть поставлены при всех возможных сочетаниях уровней факторов.

Выходной параметр, в котором характеризуется результат каждого опыта ŷ, получают путем проведения определенного количества наблюдений опытов. Так как наблюдения делаются с ошибкой, то результат каждого опыта характеризуется большим или меньшим рассеянием. По этому, прежде чем приступать к построению уравнения регрессии – модели процесса, убеждаются в однородности рассеяния результатов, характеризуемой дисперсией опытов. Если дисперсия неоднородна, необходимо увеличить количество наблюдений в опыте, а в ряде случаев изменить интервал варьирования фактора или нескольких из них или изменить методику проведения эксперимента. Построив уравнение регрессии

Задание

Исследуется процесс формирования лакокрасочного покрытия древесины на лаконаливной машине. Задача эксперимента: установить зависимость толщины покрытия от удельного расхода лака, г/м², (Х₁) и условной вязкости лака, с, (Х₂)

Нижний уровень: для Х_1min= 105 г/м², для Х_2min= 25 с.

Верхний уровень: для Х_1max= 115 г/м², для Х_2max= 5 с.

Толщина покрытия, мкм

Удельный расход, г/м²

Рис.1. График исходной зависимости

1. Методика проведения работы и соответствующие расчёты

1.1. Определение основных уровней факторов и интервалов варьирования

Таблица 1.1 - Исходные данные

Переменный фактор	Нижний уровень	Верхний уровень
X1	105 г/м2	115 г/м2
X2	25 с	30 с

Составим уравнение вида:

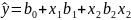
Количество опытов (N) при проведении ПФЭ зависит только от числа факторов (k) и определяется по формуле

N =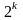 , (1.1)

где k – число переменных факторов.

В нашем случае число переменных факторов k = 2, следовательно, N = 4.

Диапазон варьирования каждого фактора

Х₁: X1 min ≤ Х₁ ≤ X1 max ; 105 ≤ Х₁ ≤ 115

X2 : X2 min ≤ Х₂ ≤ X2 max ; 25 ≤ Х₂ ≤ 35

Основной уровень фактора, за который принята середина интервала его варьирования, находится по формуле

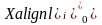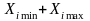= ( )/2, (1.2)

где Xi min, Xi max – значения i-го фактора на нижнем и верхнем уровнях в

натуральном виде.

Подставив значения X1 и X2 в формулу (1.2) получим

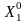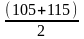= = 110 г/м² ; = =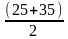 30 с

Интервал варьирования фактора определяется по формуле

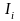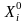= - = – ; (1.3)

где Xi min, Xi max – значения i-го фактора на нижнем и верхнем уровнях в

натуральном виде;

– основной уровень фактора.

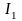max = 115 – 105 = 5 г/м²

min = 115 – 105 = 5 г/м²

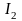max = 35 – 25 = 5 с

min = 35 – 25 = 5 с

1.2. Перевод нижних и верхних значений уровней каждого фактора в кодированный вид

№ опыта	Значение фактора
	Х1	Х2
1	Х1 max (115)	Х2 max (35)
2	Х1min (105)	Х2 max (35)
3	Х1 max (115)	Х1 min (25)
4	Х1min (105)	Х1min (25)

Перевод нижних и верхних значений уровней каждого фактора в кодированный вид производится по формуле

(1.4)

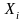где – значение i-го фактора

– основной уровень фактора;

– интервал варьирования фактора.

Х_{1 max} = (115 - 110) / 5 = 1,

Х_1min = (105 - 110) / 5 = -1.

Х_{2 max}= (35 - 30)/5= 1

Х_{2 max}= (25 - 30)/5= -1

План ПФЭ для двух факторов в кодированном виде Таблица 1,3

№ опыта	Х1	Х2
1	1	1
2	-1	1
3	1	-1
4	-1	-1