Шпоры и задачи 2012 (Саломатин) [7171 вопросов] / shpory

1. Дискретизация и квантование сигналов.

Аналоговый сигнал – сигнал, принимающий бесконечное число значений и заданный в непрерывном времени (определен для любого момента времени).Дискретный сигнал – сигнал, принимающий бесконечное число значений и заданный в дискретном времени (определен только в моменты времени, кратные периоду дискретизации Т).Цифровой сигнал – сигнал, принимающий конечное число значений, заданный в дискретном времени и представленный в виде цифровых кодов. Цифровой сигнал может быть получен из аналогового путем его дискретизации по времени (выполняется на основании теоремы отсчетов), квантования по уровню (выполняется с учетом динамического диапазона исходного аналогового сигнала) и кодирования. Под дискретизацией понимают переход от непрерывного сигнала к близкому (в определенном смысле) дискретному сигналу, описываемому разрывной функцией времени. Пример дискретного сигнала – последовательность коротких импульсов с изменяющейся амплитудой (последняя выступает в данном случае в качестве информативного параметра). Обработка и передача дискретной информации имеет ряд преимуществ по сравнению с информацией, заданной в непрерывном виде. Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи и хранения, они легко преобразуются в двоичный цифровой код и обрабатываются с помощью цифровых вычислительных устройств. Процесс дискретизации состоит обычно из двух этапов: дискретизации по времени и дискретизации (квантования) по уровню. Дискретизация аналогового сигнала по времени – процесс формирования выборки аналогового сигнала в моменты времени, кратные периоду дискретизирующей последовательности Дt. Дискретизирующая последовательность – периодическая последовательность отсчетов времени, задающая сетку дискретного времени.Период дискретизации Дt – интервал времени между двумя последовательными отсчетами аналогового сигнала (шаг дискретизации по времени).При выборе частоты дискретизации по времени можно воспользоваться теоремой В.А. Котельников. Теорема отсчетов (теорема Котельникова) – теорема, определяющая выбор периода дискретизации Дt аналогового сигнала в соответствии с его спектральной характеристикой. Согласно теореме, всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени Дt = 1/2Fmax) , где Fmax – максимальная частота в спектре сигнала. Иначе, дискретизация по времени не связана с потерей информации, если частота дискретизации fдискр = 1/Дt в два раза выше указанной верхней частоты сигнала Fmax. Согласно теореме Котельникова, нет необходимости передавать бесконечное множество всех значений непрерывного сигнала x(t), достаточно передавать лишь те его значения, которые отстоят друг от друга на расстоянии Дt = 1/(2Fmax). Для восстановления сигнала x(t) на вход идеального фильтра низких частот, имеющего полосу пропускания частот от 0 до Fmax, необходимо подать последовательность узких импульсов с амплитудой, соответствующей дискретным отсчетам сигнала x(ti) в моменты времени ti=iДt. Поскольку теорема отсчетов (теорема Котельникова) сформулирована для сигнала с ограниченным спектром, а реальные сигналы имеют неограниченную спектральную плотность, то при расчетах Дt=1/(2Fmax) используют приближенное значение Fmax (например, активную ширину спектра, определенную по амплитудному критерию, по критерию 90%- ного содержания энергии или средней мощности сигнала). Кроме того, и идеальный фильтр низких частот, необходимый для восстановления сигнала в соответствии с теоремой, является физически нереализуемым, так как предъявляемые к нему требования (идеально прямоугольная форма амплитудно-частотной характеристики, отсутствие фазового сдвига в рассматриваемой полосе частот от 0 до Fmax) оказываются противоречивыми и могут выполняться лишь с определенной погрешностью. Учитывая сказанное, частоту дискретизации по времени обычно принимают в 1,5–2,5 раза больше значения, рассчитанного по теореме Котельникова, т.е. fдискр = (3 – 5)Fmax.

Квантование (дискретизация) сигнала по уровню – процесс отображения бесконечного множества значений аналогового сигнала на некоторое конечное множество (определяемое числом уровней квантования). Отличительной особенностью дискретизации по уровню является замена непрерывной шкалы уровней сигнала x(t) дискретной шкалой xд.i(I = 1, 2,...,m), в которой различные значения сигнала отличаются между собой не менее чем на некоторое фиксированное (или выбираемое в процессе квантования) значение Дx, называемое шагом квантования. Шаг квантования – величина, равная интервалу между двумя соседними уровнями квантования (определена только для случая равномерного квантования). Необходимость квантования вызвана тем, что цифровые вычислительные устройства могут оперировать только с числами, имеющими конечное число разрядов. Таким образом, квантование представляет собой округление передаваемых значений с заданной точностью. При равномерном квантовании (Дx=const) число

разрешенных дискретных уровней xi составляет: m = ( xmax и xmin )/∆x где xmax и xmin – соответственно верхняя и нижняя границы диапазона изменения сигнала. Ошибка квантования – величина, определяемая как ж(х) = x – xд.i, где x – кодируемая дискретная величина, xд.i – дискретизированный сигнал. Шум квантования – случайная функция времени, определяемая как зависимость ошибки квантования от времени. Чем меньше значение dx, тем меньше получаемая ошибка. Если в результате квантования любое из значений сигнала х(t), попавшее в интервал (хд.i – Дх/2; хд.i + Дх/2), округляется до хд, то возникающая при этом ошибка ж(х) не превышает половины шага квантования, т.е. max|ж(х)|=0,5Дx. На практике шаг квантования dx выбирают исходя из уровня помех, в той или иной форме присутствующих при измерении, передаче и обработке реальных сигналов. Если функция x(t) заранее неизвестна, а шаг квантования Дх достаточно мал по сравнению с диапазоном изменения сигнала (xmax–xmin), то принято считать ошибку квантования ж(х) случайной величиной, подчиняющейся равномерному закону распределения. Тогда плотность вероятности f1(ж) для случайной величины ж, принимает значение 1/(Дх) внутри интервала (–Дх/2; +Дх/2) и равна нулю вне этого интервала. При Дх=const относительная погрешность квантования дx=ж(х)/x существенно зависит от текущего значения сигнала x(t). В связи с этим при необходимости обработки и передачи сигналов, изменяющихся в широком диапазоне, нередко используется неравномерное (нелинейное) квантование, когда шаг Дх принимается малым для сигналов низкого уровня и увеличивается с ростом соответствующих значений сигнала (например, Дх выбирают пропорционально логарифму значения |x(t)|). Выбор шага Дхi=xд.i–xд.i-1 осуществляется еще и с учетом плотности распределения случайного сигнала (для более вероятных значений сигнала шаг квантования выбирают меньшим, для менее вероятных – большим). Таким образом удается обеспечить высокую точность преобразования при ограниченном (не слишком большом) числе разрешенных дискретных уровней сигнала x(t).

• Гипотез : ре льные сигн лы имеют спектр s(w) сосредоточенный н конечном интерв ле.

•инитный спектр = 0 вне полосы •(- a, +a)

Соответствие ПФ

Если f(t) и s(w)– п р П , то и

Ряд Котельникова

•если подст вим Dk в s(w) и перейдем от s(w) к f(t), то

• Сигн л с финитным спектром предст вл етс без иск жени своими зн чени ми f(πk/a) – отсчет ми в дискретные моменты времени.

Шеннон • Использов л р д дл предст влени СПМ случ йного процесс

Агеев, Слепян • Теорем . ункци с финитным спектром [– ɛ,+ ɛ] может с любой точностью

Аппроксимиров ть н з д нном отрезке [– T, T] непрерывную функцию спектр которой н ходитс

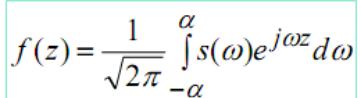
3.Cвойства функций с финитным спектром

•Теория целых функций t  z-Комплексная переменная z заменяет переменную t

.

•Функция f(t) становится аналитической в любой ограниченной области

комплексной переменной

Пэли и Винер

•При |z| ∞ , f(z) возрастает не быстрее exp { az }, т.е. является целой функцией экспоненциального роста.

•Всякая целая функция экспоненциального роста имеет финитный спектр.

4. задача интерполяции-восстановления. Методы получения интерполяционных рядов

•Задача интерполяции-восстановления заданной функции на бесконечной последовательности Еѐ элементов (например, производных)

•Уиттекер – в качестве элементов использовал значения функции в равноотстоящих точках.

•Если расстояние <= ( π/ a) то решение однозначное и задается рядом (*) при t  z.

Линейная интерполяция

Задача восстановления аналогового сигнала по его дискретным отсчѐтам, с точки зрения математики, это не что иное, как хорошо известная задача интерполяции непрерывной функции F(x) по конечному числу N еѐ точек X0, X1,… Xi,… XN. Эти точки, в которых значение функции задано, называются узлами интерполяции. Поскольку в общем случае характер интерполируемой функции заранее неизвестен, то обычно задача интерполяции сводится к задаче кусочной аппроксимации: необходимо подобрать простые аналитические функции, которые будут считаться приближениями к исходной функции между узлами. В самих узлах значения аппроксимирующих функций должны совпадать с заданными значениями исходной функции. Самым простым решением будет аппроксимация линейными функциями вида fi(x)=a+b(x-Xi). Геометрически такая интерполяция представляет из себя ломаную линию, состоящую из соединѐнных в узлах прямолинейных отрезков:

Интерполяция полиномами, проблема звона

Угловатый вид линейной интерполяции сразу наводит на мысли, что это не самое точное представление исходного сигнала. Действительно, мы знаем, что полоса пропускания измерительного тракта ограничена. Спектр же изображѐнной на рисунке выше остроугольной осциллограммы бесконечен. Следовательно, более верным представлением будет аппроксимация более гладкой функцией.

Такое решение даѐт, например, метод интерполяции кусочно-кубическими функциями. Идея метода состоит в том, что исходная функция на каждом отрезке [Xi, Xi+1] аппроксимируется многочленом третьей степени (т.е. функцией вида fi(x)=a+b(x-Xi)+c(x-Xi)2+d(x-Xi)3), при этом в узлах совпадают не только значения соседних многочленов, но и их первые производные (т.е. fi(Xi+1)=fi+1(Xi+1) и f’i(Xi+1)=f’i+1(Xi+1)). Значения производных интерполирующих многочленов выбираются произвольно, исходя из дополнительной информации о характере исходной функции. Если никакой дополнительной информации нет, то обычно в качестве значений производных используются разделѐнные разности: f’(Xi)=(F(Xi+1)-F(Xi))/(Xi+1-Xi).

Выполнение условия непрерывности производной гарантирует гладкость итоговой осциллограммы, но вызывает неприятный побочный эффект, называемый эффектом звона.

Сумма представляет собой Суперпозицию наложения подобных слагаемых.

7.Дискретизация узкополосных сигналов с несущей частотой

Дискретизация с использованием аналитического сигнала

Базисы дискретизации и Восстановления

Отсчеты сигнала

k

Ua ( fH fB )

Дискретизация на гармониках

8.Модель и показатели АЦП

Назначение элементов дискретной системы

Входной ФНЧ или ПФ: Предотвращение наложения спектров Аналого цифровой преобразователь (АЦП): 1.Дискретизация сигнала во времени 2.Квантование сигнала по уровню 3.Цифровое кодирование отсчетов сигнала

Цифро аналоговый преобразователь (ЦАП):1.Преобразование цифровых кодов в сигнал 2.Выходной ФНЧ или ПФ,3.Восстановление (сглаживание) сигнала Аналоговый сигнал – непрерывен во времени и по амплитуде

Дискретный сигнал непрерывен по амплитуде, но определяется только в дискретных то чках времени Цифровой сигнал – дискретный во времени сигнал с дискретной амплитудой

Показатели АЦП

Основные характеристики АЦП:

Гармонические искажения,Наихудшие гармоники,Отношение сигнал шум (SNR),Отношен ие сигнал шум + искажения (SINAD),Эффективное число разрядов (ENOB),Аналоговая по лоса пропускания,Динамический диапазон, свободный от гармоник (SFDR),Двух и многот ональные интермодуляционные искажения