§8. Задачи.

Задача 1. Старая система координат преобразуется к новой системе , заданной следующими углами: , , , . Написать матрицу преобразования и проверить ее ортогональные свойства.

Решение. Имеем:

, ,

, ,

,

, ,

.

Матрица преобразования будет иметь вид: (52)

Ортогональность ее строк и столбцов проверяется непосредственно.

Задача 2. Пусть новая система координат получена из старой в результате вращения вокруг оси на угол против часовой стрелки. Написать матрицу преобразования.

Решение.

, ,

,

, ,

,

, ,

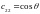Тогда матрица преобразования имеет

вид: (53)

Задача 3. Исследовать влияние преобразования координат

на компоненты вектора.

Решение. Это преобразование координат называется инверсией (отражением) относительно плоскости . Первоначальная правая система координат преобразуется в левую . Матрица преобразования имеет вид: (54)

Вектор преобразуется по формуле (40):

(55)

или

Таким образом, указанная инверсия изменяет только компоненту , две другие компоненты при этом не меняются.

Задача 4. Найти преобразование компонент вектора при вращении, описанном в задаче 2.

Решение. Используя матрицу преобразования (53) и формулу (55), получим:

(56)

Задача 5.. Доказать равенство (57)

Решение. Имеем:

Задача 6. Компоненты единичного вектора являются непрерывно дифференцируемыми функциями параметра . Показать, что вектор перпендикулярен вектору .

Решение. Необходимо доказать, что скалярное произведение . Имеем:

Задача 7. Доказать, что каждый элемент ортогональной матрицы преобразования равен своему алгебраическому дополнению, взятому со знаком плюс или минус.

Решение. Матрица перехода от старой системы координат к новой имеет вид (15). Ее определитель, как было показано в параграфе 3, равен , где знак плюс берется в том случае, если старая и новая системы координат имеют одинаковую ориентацию (например, обе правые) и знак минус – в противном случае. По определению обратной матрицы имеем:

где – алгебраическое дополнение элементов матрицы . С другой стороны, как было показано в параграфе 3, обратная матрица получается транспонированием прямой матрицы, т.е. и имеет вид (17). Отсюда и получаем, что .

Подчеркнем еще раз, что знак плюс берется тогда, когда обе системы координат, старая и новая, имеют одинаковую ориентацию и знак минус – в противном случае.

§9. Тензор второго ранга.

Вспомним задачу, приведшую нас в параграфе 1 к понятию тензора напряжений, и формулу (12). Сравним ее с формулой (51). Формула (51) любому направлению в пространстве сопоставляет скаляр , который мы назвали проекцией вектора на направление . Формула (12) идентична по структуре формуле (51), но с ее помощью любому направлению в пространстве сопоставляется не скаляр, а вектор тоже посредством линейного и однородного относительно направляющих косинусов соотношения. Из этого и будем исходить. Итак, пусть любому направлению в пространстве сопоставляется вектор с помощью линейного и однородного относительно направляющих косинусов соотношения:

(58)

Геометрический объект с таким свойством называется тензором второго ранга и обозначается . Вектор называется проекцией тензора на направление или значением тензора в этом направлении. Выясним, какой смысл имеют векторы , , в формуле (58). Для этого совместим направление с направлением оси . Тогда , , . Получаем, что проекция тензора на ось равна вектору . Аналогично, совмещая направление с направлением осей и , получим, что векторы и суть проекции тензора на оси и . Таким образом, в любой прямоугольной системе координат тензор задается тремя векторами , , – своими проекциями на базисные направления. Компоненты векторов , , в системе координат обозначим , , .

Девять величин называются компонентами тензора в системе координат . Расположим их в виде матрицы:

, (59)

которая называется матрицей тензора. Столбцы матрицы определяют три проекции тензора на координатные оси.

В другой системе координат тензор также определяется тремя проекциями , , на новые координатные оси. Проекции тензора в новой и старой системах координат связаны друг с другом. Установим эту связь. Совместим в (58) направление с направлением оси . Получим проекцию тензора на ось :

(60)

Совместив с направлением оси , получим

, (61)

и наконец:

(62)

Стоящие в этих формулах косинусы – это элементы матрицы преобразования . Поэтому можно переписать:

(63)

.

Сокращенно это записывается так:

, , (64)

или еще короче: (65)

Видим, что закон преобразования проекций тензора такой же, как закон преобразования проекций вектора. Матрица тензора в новой системе координат состоит из компонент проекций тензора на эти новые оси. Первая проекция – вектор в новой системе имеет компоненты: . Аналогично и . Составленная из них матрица:

(66)

называется матрицей тензора в новой системе координат. Таким образом, матрица тензора в старой системе состоит из компонент проекций тензора на старые оси, а в новой системе – из компонент проекций тензора на новые оси.

Установим связь между компонентами тензора в старой и новой системах координат. Обозначим компоненты векторов в новом базисе через , т.е. . Компоненты векторов в новом базисе выразим через старые по формулам преобразования вектора:

(67)

Тогда первое равенство (64) в новых координатах запишется так:

(68)

Аналогично, две другие формулы (64) в новых координатах будут выглядеть так:

(69)

Или объединяя все три формулы:

(70)

По формуле (70) преобразуются компоненты тензора при переходе от старой системы координат к новой. Выведем обратную формулу. Умножим обе части (70) на , воспользуемся ортогональностью матрицы перехода и свойством символа Кронекера:

(71)

Умножим теперь обе части на :

или (72)

Формулы (70) и (72) определяют закон преобразования тензора второго ранга. Они положены в основу второго определения тензора. В любой прямоугольной системе координат тензор 2-го ранга определяется девятью компонентами, которые при преобразовании системы координат преобразуются по формулам (70) и (72).