§ 2. Транспортная задача линейного программирования

Основные понятия

Открытая и закрытая транспортные задачи линейного программирования. Задающая таблица (таблица для записи условий) транспортной задачи линейного программирования. Условия разрешимости. Примеры практических задач, приводящих к транспортной задаче линейного программирования. Построение начального плана методом северо-западного угла и методом наименьшего тарифа. Признак оптимальности. Распределительный метод. Метод потенциалов. Экономическая интерпретация потенциалов.

ЛИТЕРАТУРА: (1).

Вопросы для самопроверки

1. Является ли открытой следующая транспортная задача линейного программирования.

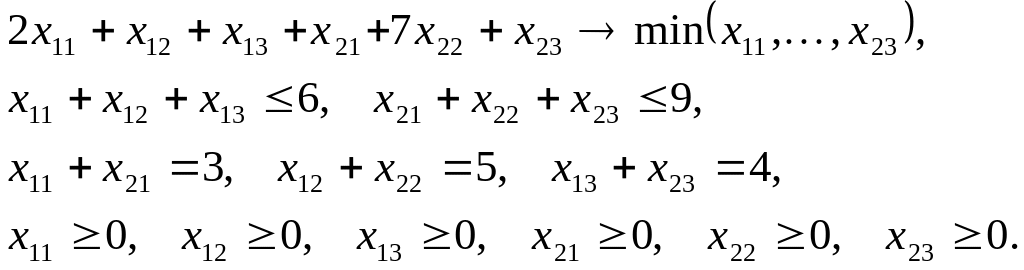(1)

2. Для задачи (1) составьте заданную таблицу.

4. Каковы необходимые и достаточые условия разрешимости транспортной задачи линейного программирования?

5. Имеет ли решение задача (1)?

6. Как установить оптимальность плана?

7. Для любого ли допустимого плана транспортной задачи линейного программирования существует система потенциалов?

8. Приведите задачу (1) к закрытой транспортной задаче.

Вычислительная схема метода потенциалов.

Метод потенциалов - один из методов решения задачи

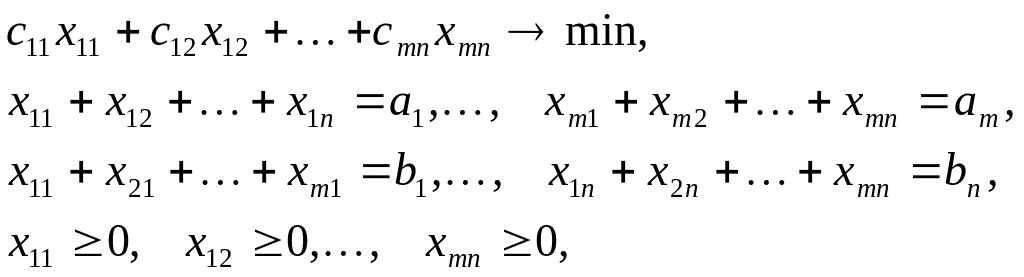(2)

где x₁₁, x₁₂,…, x_mn - переменные; c₁₁, c₁₂,..., c_mn – произвольные фиксированные числа, которые будем называть тарифами; a₁,... ,a_m, b₁,..., b_n - положительные фиксированные числа, удовлетворяющие условию .

Рассмотрим вычислительную схему метода потенциалов, в которой для решения задачи (2) строится последовательность таблиц Т₁,..., Т_k до тех пор, пока не получится таблица Т_k, удовлетворяющая определенному условию. Все таблицы имеют m cтрок и n столбцов; во всех клетках этих таблиц в правом верхнем углу записаны соответствующие тарифы (в клетке(i, j) - тариф c_ij). В каждой из этих таблиц имеется ровно m+n-1 клеток, в которых кроме тарифов записано еще по одному неотрицательному числу (эти числа будем называть перевозками). Клетки, в которых записаны перевозки, будем называть заполненными; остальные клетки будем называть свободными. В последней таблице Т_k содержится информация о решении задачи (2), которое получается так: х_ij=d_ij, если клетка (i,j) таблицы Т_k заполнена перевозкой d_ij; в противном случае х_ij=0 (i=1,...,m; j=1,...,n). Помимо записи тарифов в углы клеток при составлении любой из таблиц Т₁,...,Т_k, кроме последней, производим следующие шесть действий.

1. Заполняем таблицу перевозками. Первую таблицу Т₁ заполняем специальным образом (как именно, сказано ниже). Каждую последующую таблицу заполняем так: перевозки из непомеченных клеток предыдущей таблицы переписываем в соответствующие клетки заполняемой таблицы без изменения, а перевозки из помеченных плюсом (минусом) клеток переписываем в соответствующие клетки увеличенными (уменьшенными) на величину главной перевозки; исключение из сказанного составляет лишь главная перевозка – она переписывается без изменения в ту клетку заполняемой таблицы, которая соответствует плохой клетке предыдущей таблицы.

2. Вычисляем потенциалы строк и столбцов, т.е. такие числа u₁,..., u_m, v₁,..., v_n, что u₁=0 и u_i+v_j=c_ij для каждой заполненной клетки (i, j). Потенциалы u₁,..., u_m записываем справа от соответствующих строк таблицы, а потенциалы v₁,..., v_n - под соответствующими столбцами. Вычисляем потенциалы последовательно (постепенно). Сначала вычисляем потенциал u₁=0. Затем отыскиваем какую-нибудь такую заполненную клетку (i, j), для которой уже вычислен только один из потенциалов u_i или v_j, и вычисляем другой из них по формуле v_j=c_ij–u_i или u_i=c_ij–v_j. Затем опять отыскиваем какую-нибудь обладающую указанным свойством клетку и вычисляем соответствующий потенциал и т.д. до тех пор, пока не будут найдены все потенциалы.

3. Определяем и помечаем знаком плюс плохую клетку, т.е. какую-нибудь одну такую свободную клетку (i, j), для которой c_ij–ui–v_j<0.

4. Находим цикл пересчета, т.е. такой замкнутый путь, который проходит по строкам и столбцам и имеет повороты на 90° только в заполненных и плохой клетках (не обязательно, чтобы этот путь имел повороты во всех заполненных клетках, но обязательно он должен иметь поворот в плохой клетке).

5. Означиваем цикл пересчета, т.е. снабжаем его повороты знаком плюс или минус так, чтобы поворот в плохой клетке был помечен знаком плюс (этот плюс уже был поставлен при определении плохой клетки) и никакие два соседних поворота не оказались помеченными одноименными знаками.

6. Определяем и заключаем в круглые скобки главную перевозку, т.е. наименьшую из перевозок, расположенных в помеченных минусом клетках (если таких наименьших перевозок несколько, то в качестве главной можно выбрать любую из них).

Как уже говорилось,все шесть перечисленных действий выполняются при составлении любой таблицы, кроме последней. Последняя таблица Т_k характеризуется тем, что в ней нет ни одной свободной клетки (i,j), для которой разность между её тарифом c_ij и потенциалами u_i, v_j отрицательна. Поэтому для последней таблицы указанные действия заканчиваются на попытке определить плохую клетку.

Перевозки, которые нужно записать в таблицу T₁, вычисляем так. Заготавливаем вспомогательную пустую таблицу из m строк и n столбцов и для каждого i=1,..., m справа от i-й строки этой таблицы записываем число a_i, а для каждого j=1,..., n под j-м столбцом записываем число b_j. После этого делаем m+n-1 шагов заполнения вспомогательной таблицы. Каждый такой шаг состоит из следующей последовательности действий: 1) определяется наименьший номер i-й строки, справа от которой имеется незачеркнутое число (обозначим это число через а); 2) определяется наименьший номер j столбца, под которым имеется незачеркнутое число (обозначим это число через b); 3)если , то число b записывается в клетку (i, j), затем незачеркнутое число справа от i-той строки и незачеркнутое число под j-м столбцом зачеркиваются и справа от i-той строки (после зачеркнутого числа) записывается число a-b, а если a<b, то число а записывается в клетку (i, j), затем незачеркнутое число справа от i-й строки и незачеркнутое число под j-м столбцом зачеркиваются и под j-м столбцом (под зачеркнутым числом) записывается число b-a. В итоге во вспомогательной таблице появляются m+n-1 чисел, которые нужно переписать в соответствующие клетки таблицы Т₁.

Пример 1. Решить задачу линейного програмирования

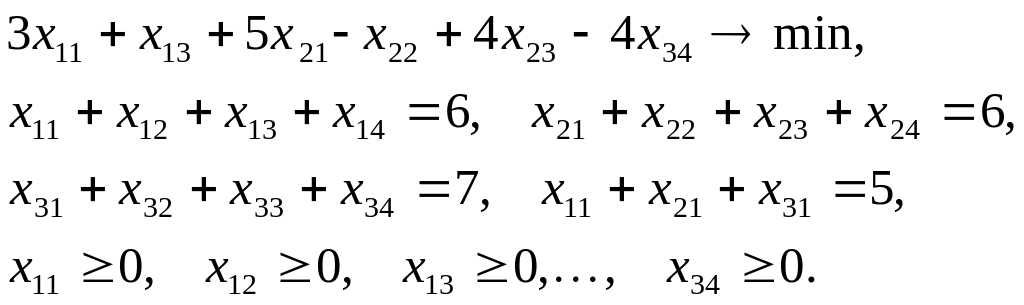
Сравнивая эту задачу с задачей (2), заключаем, что в данном случае m=3, n=4, c₁₁=3, c₁₂=0, c₁₃=1, c₁₄=0, c₂₁=5, c₂₂=-1, c₂₃=4, c₂₄=c₃₁=c₃₂=с₃₃=0, c₃₄=–4, a₁=a₂=6, a₃=7, b₁=5, b₂=1, b₃=4, b₄=9.

Решение начинаем с составления вспомогательной таблицы, справа от соответствующих строк которой записываем числа 6, 6, 7, a под соответствующими столбцами - числа 5, 1, 4, 9. Делаем первый шаг заполнения этой таблицы. Справа от первой строки имеется незачёркнутое число 6, поэтому i=1, a=6; под первым столбцом имеется незачёркнутое число 5, поэтому j=1, b=5. Так как , то в клетку (1,1) записываем число 5, число 6 справа от первой строки и число 5 под первым столбцом зачёркиваем и справа от 1-й строки после зачёркнутого числа записываем число 1, равное разности a–b. Делаем второй шаг. Теперь справа от первой строки имеется незачёркнутое число 1, поэтому i=1, a=1;под первым столбцом нет незачёркнутых чисел, а под 2-м столбцом имеется незачеpкнутое число 1, поэтому j=2, b=1. Так как , то в клетку (1,2) записываем число 1, число 1 справа от 1-й строки и число 1 под 2-м столбцом зачеркиваем и справа от 1-й строки после зачеркнутого числа 1 записываем число 0, равное разности a–b. Затем делаем еще четыре шага, в результате чего получаем таблицу, которая вместе с выписанными около нее числами выглядит так (из-за типографских затруднений вместо зачеркивания употреблено заключение в круглые скобки):

5	1	0		(6)	(1)	(0)
		4	2	(6)	(2)
			7	(7)	0
(5)	(1)	(4)	(9)
		(4)	(7)

Числа из этой таблицы переписываем в соответствующие клетки таблицы Т₁ и приступаем к вычислению потенциалов. Справа от первой строки таблицы Т₁ записываем потенциал u₁=0. Затем находим заполненую клетку (1,3), для которой уже вычислен потенциал u₁ и не вычислен потенциал v₃, и вычисляем v₃ по формуле . Затем находим заполненную клетку (2,3), для которой вычислен потенциал u₂, и вычисляем u₂ по формуле . Аналогично вычисляем остальные потенциалы.

_{таблица Т1}

		3		0				1		0	u1=0
5―			1			0+
	5			―1				4		0	u2=3
						(4)―			2+
	0				0		0			―4	u3=―1
									7―
v1=3			v2=0			v3=1			v4=―3

Определяем и помечаем знаком плюс плохую клетку. В качестве плохой можно выбрать, например, свободную клетку (3.1), так как . После этого находим цикл пересчёта, имеющий повороты в клетках (3, 1), (3, 4), (2, 4), (2, 3), (1, 3), (1, 1). Затем означиваем этот цикл: начиная с плохой клетки (3, 1), движемся по циклу и поочерёдно помечаем его повороты знаками плюс и минус (поворот в плохой клетке уже был помечен плюсом при нахождении этой клетки). Составление таблицы Т₁ заканчиваем нахождением и заключением в круглые скобки главной перевозки 4, расположенной в клетке (2, 3).

Заполняем вторую таблицу. Перевозку 1 из непомеченной клетки (1, 2) таблицы Т₁ переписываем без изменения в клетку (1,2) таблицы Т₂ Перевозки 0,2 из помеченных плюсом клеток (1,3), (2,4) таблицы Т₁ увеличиваем на 4 и записываем в клетки (1,3), (2,4) таблицы Т₂. Перевозки 5,7 из помеченных минусом клеток (1,1), (3,4) таблицы Т₁ уменьшаем на 4 и записываем в клетки (1,1), (3,4) таблицы Т₂. Главную перевозку 4 из клетки (2,3) таблицы Т₁ записываем в клетку (3,1) таблицы Т₂. После этого для таблицы Т₂ вычисляем потенциалы, определяем и помечаем знаком плюс плохую клетку (2,2), находим и означиваем цикл пересчета, определяем и заключаем в круглые скобки главную перевозку 1 в клетке (1,2).

Таблица Т₂

		3		0				1		0	u1=0
1+			(1)―			4
	5			―1				4		0	u2=1
									6―
	0				0		0			―4	u3=―3
4―									3+
v1=3			v2=0			v3=1			v4=―1

Заполняем таблицу Т₃ и вычисляем для неё потенциалы .

_{Таблица Т3}

		3		0				1		0	u1=0
2						4
	5			―1				4		0	u2=1
			1						5
	0				0		0			―4	u3=―3
3									4
v1=3			v2=―2			v3=1			v4=―1

Далее, пытаясь определить в таблице Т₃ плохую клетку, устанавливаем, что сделать это не удаётся, так как для любой свободной клетки разность между её тарифом и потенциалами не является отрицательной. Такая ситуация говорит о том, что построение таблиц закончено. Из последней таблицы получаем решение задачи:

,

,

.

Замечание 1. Уже отмечалось, что потенциалы u₁,..., u_m записываются справа от соответствующих строк таблицы, а потенциалы v₁,..., v_n - под соответствующими столбцами. При этом не обязательно указывать численные значения потенциалов с помощью равенств, как это было сделано в рассмотренном выше примере; достаточно ограничиться записью только самих численных значений, как это сделано ниже при решении задачи из примера 2.

Пример 2. Решить задачу вида (2), положив m=4, n=6, c₁₁=1, c₁₂=0, c₁₃=c₁₄=c₁₅=c₁₆=c₂₁=c₂₂=2, c₂₃=0, c₂₄=-4, c₂₅=3, c₂₆=-4, c₃₁=-2, c₃₂=c₃₃=1, c₃₄=0, c₃₅=-3, c₃₆=c₄₁=c₄₂=4, c₄₃=0, c₄₄=-3, с₄₅=0, c₄₆=-3, a₁=a₂=9, a₃=a₄=3, b₁=b₂=4, b₃=5, b₄=8, b₅=2, b₆=1.

Решаем методом потенциалов (как и в пpимеpе 1, вместо зачеpкивания чисел около вспомогательной таблицы употpеблено заключение их в кpуглые скобки).

4	4	1				(9)	(5)	(1)
		4	5			(9)	(5)
			3	0		(3)	(0)
				2	1	(3)	(1)	0
(4)	(4)	(5)	(8)	(2)	(1)
		(4)	(3)	(2)

Таблица Т₁

		1		0				2		2		2		2	0
4―			4			1+
	2			2				0		―4		3		―4	―2
						4―			5+
	―2				1		1			0		―3		4	2
+									(3)―		0
	4				4		0			―3		0		3	5
											2		1
1			0			2			―2		―5		―8

_{Таблица Т2}

		1		0				2		2		2		2	0
1+			4			4―
	2			2				0		―4		3		―4	―2
						1			8
	―2				1		1			0		―3		4	―3
3―											0+
	4				4		0			―3		0		3	0
						+					(2)		1
1			0			2			―2		0		―3

_{Таблица Т3}

		1		0				2		2		2		2	0
3			4			2
	2			2				0		―4		3		―4	―2
						(1)―			8				+
	2				1		1			0		―3		4	―3
1											2
	4				4		0			―3		0		3	―2
						2+							1―
1			0			2			―2		0		―1

_{Таблица Т4}

		1		0				2		2		2		2	0
3			4			2
	2			2				0		―4		3		―4	―3
									8				1
	―2				1		1			0		―3		4	―3
1											2
	4				4		0			―3		0		―3	―2
						3
1			0			2			―1		0		―1

,

,

,

.

Замечание 2. Иногда нахождение цикла пересчета в таблице Тv представляется затруднительным. Преодолеть это затруднение можно так. Заготавливаем на черновике пустую таблицу размером m*n и отмечаем в ней точками центры тех клеток, которые соответствуют заполненным и плохой клетками таблицы Т_v. После этого просматриваем все отмеченные незачеркнутые точками клетки и зачеркиваем крестиком те точки, которые в момент зачеркивания либо в своей строке не имеют других незачеркнутых точек. Затем опять просматриваем все отмеченные незачеркнутыми точками клетки и зачеркиваем нужные точки и т.д.. Эта процедура продолжается до тех пор, пока при очередном просмотре всех клеток с незачеркнутыми точками не будет зачеркнуто ни одной точки. В результате незачеркнутыми оказываются точки только в тех клетках, в которых цикл пересчета делает повороты, причем в каждой строке и каждом столбце имеется либо ровно две незачеркнутые точки, либо ни одной, так что нахождение цикла не составляет труда. Например, если проделать все сказанное для таблицы Т₂ из примера 2, то получится такой pезультат (пунктиром показан цикл пересчета):

Замечание 3. Вообще говоря, в таблицах имеется по нескольку клеток, каждую из которых можно выбрать в качестве плохой. Если задача имеет не единственное решение, то допустимый произвол в выборе плохих клеток может привести к разным оптимальным планам. Сказанное справедливо и в отношении возможного произвола в выборе главных перевозок.