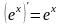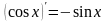Дифференциальное исчисление

Производной функции 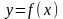в точке называется предел отношения приращения функции к приращению аргумента , при условии, что приращение аргумента стремится к нулю:

.

Правила дифференцирования

Пусть заданы дифференцируемые функции и , тогда:

1) 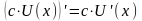, где c=const

2)

3)

4)

Таблица производных элементарных функций

Производная сложной функции

Если , где , то функция называется сложной.

Например, , где , то получим сложную функцию .

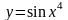Производная сложной функции находиться по формуле: .

Производные высших порядков

Пусть дана функция . Производная также является функцией от аргумента х и называется производной первого порядка.

Если функция дифференцируема, то ее производная называется производной второго порядка и обозначается или .

Производная от производной второго порядка называется производной третьего порядка и обозначается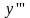 или .

Производной n-го порядка (или n-ой производной) называется производная от производной (n-1) порядка.

Производные порядка выше первого называются производными высших порядков.

Вычисление производных функций

Пример 1. Найти производную функции

Решение:

Это простейший пример его можно найти в таблице производных элементарных функций. Посмотрим на решение и проанализируйте его, что же произошло? А произошла следующая вещь: была функция  , которая в результате решения превратилась в функцию  .

То есть, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. В таблице производных функции превращаются в другие функции. Единственным исключением является экспоненциальная функция  , которая превращается сама в себя. Операция нахождения производной называетсядифференцированием.

ВНИМАНИЕ, ВАЖНО! Забыть поставить штрих (там, где надо), либо нарисовать лишний штрих (там, где не надо) – ГРУБАЯ ОШИБКА! Функция и её производная – это две разные функции!

Из таблицы производных желательно запомнить наизусть правила дифференцирования и производные некоторых элементарных функций, особенно:

производную константы: ;

производную степенной функции: ,

в частности: , , .

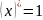Зачем запоминать? Данные знания являются элементарными знаниями о производных. И это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда сталкиваешься с производными.

Обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.

Рассмотрим правил дифференцирования:

1. Постоянное число можно (и нужно) вынести за знак производной

Пример 2. Найти производную функции

Решение:

Посмотреть в таблицу производных. Производная косинуса там есть, но у нас .

Используем правило, выносим постоянный множитель за знак производной:

А теперь превращаем косинус по таблице:

Результат необходимо немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:

.