Вопрос 10. Теоретико-множественный смысл разности двух целых неотрицательных чисел. Условие существования разности на множестве целых неотрицательных чисел (с доказательством). Правила вычитания числа из суммы и суммы из числа, их теоретико-множественная интерпретация (с доказательством).

Определение. Разностью двух целых неотрицательных чисел а и в называется количество элементов в дополнении множества В до множества А, при условии, что а=п(А), в=п(В), ВА.

а-в=n(А/В), где а=n(А), в=n(В) и В А

1) Объясним теоретико-множественный смысл разности 5 и 3

Пусть А= {а, в, с, d, е}, n(А)=5,

В= {а, в, с}, n(В)=3, ВА

Найдём А/В= {d, е}, где n(А/В) = 5-3=2 (по определению разности на множестве целых неотрицательных чисел).

2) Объясним теоретико-множественный смысл разности 3 и 0.

Пусть А= {а, в, с}, n(А)=3,

В - «множество натуральных корней уравнения 4х+7=0», n(В)=0, ВА

Найдём А/В= {а, в, с}, где

n(А/В) = 3-0=3 (по определению разности на множестве целых неотрицательных чисел).

3) Объясним теоретико-множественный смысл разности 3 и 3.

Пусть А= {а, в, с}, n(А)=3,

В = {а, в, с}, n(В)=3, ВА

Найдём А/В= {}, где

n(А/В) = 3-3=0 (по определению разности на множестве целых неотрицательных чисел).

Теорема. Результат вычитания не зависит от выбора множеств.

Пример.

1. Во дворе гуляли 5 детей. 3 ребёнка ушли домой. Сколько детей осталось гулять во дворе? Решение: 5-3=2(д.).

2. За два дня туристы должны были пройти 5км. В первый день туристы прошли 3км. Сколько километров осталось пройти туристам? Решение: 2+3=5(км).

3. В гараже было 5 автомобилей. Утром из гаража выехало 3 автомобиля. Сколько автомобилей осталось в гараже? Решение: 5-3=2(авт.).

Теорема (условие существования разности). Для того, чтобы разность а и в существовала, необходимо и достаточно, чтобы в было не больше а.

Необходимое условие.

Дано: а-в – существует.

Доказать: ва.

Доказательство: а-в=n(А/В) (по определению разности), где а=n(А), в=n(В) и

В А ва. (по определению данного отношения)

Достаточное условие.

Дано: ва.

Доказать: а-в – существует.

Доказательство: ва  (по определению данного отношения) а=n(А), в=n(В) и

В А если множество В содержится в множестве А, то существует множество, которое дополняет В до А, то есть А/В (по определению операции дополнения) а если существует множество А/В, значит существует и кол-во элементов в нём n(А/В) а если есть кол-во элементов в дополнении, значит есть и разность, соответствующая ему n(А/В)=а-в, где а=n(А), в=n(В).

Теорема. Если разность существует, то она единственная.

Дано: а-в – существует.

Доказать: а-в – единственная.

Доказательство. Предположим, что разность а и в не единственная. Пусть и , где 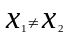. Тогда и (зависимость между компонентами и результатом действия вычитания) Левые части равенств равны, значит, равны и правые части равенства (теорема о равенстве) =  Суммы равны, одно из слагаемых равно  . Мы пришли к противоречию с выдвинутым предположением ( ), следовательно, наше предположение неверно. Если разность существует, то она единственная.

Правило вычитания из суммы числа

(а+в)-с=(а-с)+в=а+(в-с)

Дано:

Доказать: (а+в)-с=(а-с)+в

Доказательство:

1. а+в=п(АВ), где АВ= (по определению суммы на ).

2. (а+в)-с= п(АВ)- п(С)= п((АВ)/C), где С(АВ) (по определению разности на ).

3. а-с= n(А/С), где СА(по определению разности на ).

4. (а-с)+в= n(А/С)+ п(В)= п((А/C)В), где (А/C)В=, (по определению суммы на )

5. Сравним множества (АВ)/C и (А/C)В

Множества конечные и они равны, следовательно, равны и кол-ва элементов в них п((АВ)/C)= п((А/C)В), а если правые части равенств равны, то равны и левые части равенств (а+в)-с=(а-с)+в.

Правило вычитания из числа суммы

а-(в+с)=(а-в)-с=(а-с)-в

Дано:

Доказать: а-(в+с)=(а-в)-с

Доказательство:

1) в+с=п(ВС), где ВС= (по определению суммы на ).

2) а-(в+с)= п(А)-п(ВС)= п(А/(ВC)), где (ВС)А (по определению разности на ).

3) а-в= n(А/В), где ВА(по определению разности на ).

4) (а-в)-с= n(А/В)- п(С)= п((А/В)/С), где С(А/В), (по определению разности на )

Сравним множества А/(ВC), и (А/В)/С

Множества конечные и они равны, следовательно, равны и кол-ва элементов в них п(А/(ВC))= п((А/В)/С), а если правые части равенств равны, то равны и левые части равенств а-(в+с)=(а-в)-с.

Определение разности через сумму.

А=В(А/В), где В(А/В)=

п(А)=п(В(А/В)), по определению суммы на ,

п(А)=п(В)+п(А/В), обозначим п(А)=а, п(В)=в, п(А/В)=с,

тогда получим определение разности.

Разностью двух целых неотрицательных чисел а и в называется такое целое неотрицательное число с, которое, будучи сложенным с в даст а.

а-в=сс+в=а, где ва, а,в,с

Пример. 5-3=22+3=5, где 35, 3,5,2

5-5=00+5=5, где 55, 5,0

5-0=55+0=5, где 05, 5,0