Дополнение. Глубина вложенности подформулы в формулу
Определение. Пусть
-
формулы, а
- какая-то ее подформула. Глубина
вложенности подформулы
в формулу
,
обозначаемая
,
определяется следующим образом:
если
,
то
;
по определению также принимается, что
если формула
вообще не входит в
,
то и в этом случае
;если
,
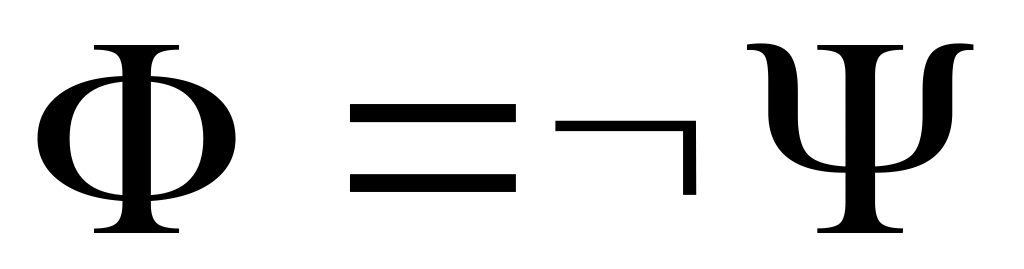и
,
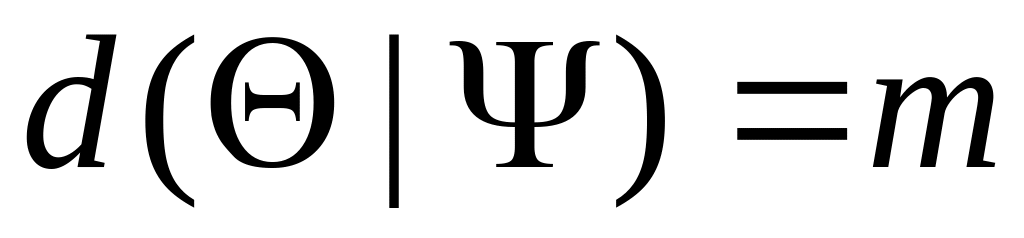то
,если
,
то
.
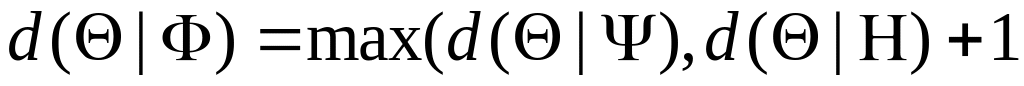Из этого определения понятно, что число равно максимальной длине пути в дереве, представляющем формулу от корня до узла, являющегося корнем поддерева, представляющего формулу (таких поддеревьев может быть несколько).
Пусть в условиях предыдущего определения
запись
обозначает формулу, полученную из
заменой некоторых (всех, в частности)
вхождений подформулы
эквивалентной ей формулой
.
При этом, если
не входит в
,
то формула
считается совпадающей с формулой
.
Утверждение. Для произвольного
набора
значений переменных
.
Доказательство. Индукция по глубине .
Базис.
,
т.е. либо
,
т.е.,
,
и значения этих формул – как эквивалентных
- совпадают на любом наборе
;
либо
,
и тогда доказывать нечего.
Предположение. Пусть утверждение
верно при любой глубине
.
Переход. Полагаем
.
Тогда, если
,
то
,
и по предположению индукции для любого
имеем
.
Переходя к отрицанию, получим тот же
результат и для формулы
.
Если же
,
то, поскольку
,
то по предположению индукции
,
что и требовалось.
1 Таким образом, если ├ T , то каждая формула соответствующего вывода есть либо аксиома, либо элемент множества , либо получена применением некоторого правила вывода к ранее полученным формулам. Иначе говоря, при ├ T можно считать множество определенным с точностью до любого (добавляемого) подмножества аксиом.
2 При изложении исчисления высказываний предполагается знакомство читателя с теорией булевых функций в объеме гл. 6 учебника «Дискретная математика» (вып. XIX в серии «Математика в техническом университете»).
3 Ниже в записи формул опущены внешние скобки.
4 См. следствие 1 и пример доказательства формулы A A.
5 Далее для краткости мы пишем знак равенства между формулами, читая запись = как «формула есть формула » (совпадает с ней).
6 Как и в случае 2.2, можно поступить так: (), после чего получаем .
7 Строго говоря, это надо доказывать индукцией по «глубине вложенности» подформулы в формулу (см. Дополнение ниже).