4. Нахождение нулей и полюсов системы

Рассмотрим передаточную функцию для замкнутой системы:

Так как числитель данной функции является числом, это значит, что нулей у данной функции нет. Найдем полюса в данной системе, для этого найдем корни характеристического уравнения, т.е. знаменателя передаточной функции:

(3)

Положение корней на комплексной плоскости определяет устойчивость системы, корни (3). В численном виде:

Корни данного уравнения:

Отобразим вычисленные полюса на комплексной плоскости, изображенной на рисунке 7.

Рисунок 7 – Корни характеристического уравнения на комплексной плоскости

Если корни характеристического уравнения все вещественные отрицательные, то система устойчива.

5. Определение устойчивости системы по критериям Найквиста, Гурвица, Михайлова.

Устойчивость – свойство системы автоматического управления (САУ) возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения. Устойчивая САУ – система, в которой переходные процессы являются затухающими [1].

Приведем проверку устойчивости по трем критериям: Найквиста, Михайлова и Гурвица.

5.1 Устойчивость по критерию Найквиста

Для устойчивости замкнутой системы необходимо и достаточно чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами {-1, j0}.

Годограф Найквиста представлен на рисунке 8.

Рисунок 8 – Годограф Найквиста для разомкнутой САУ

Условия границы устойчивости по критерию Найквиста: при K=K_max вектор W(j ) = -1+j0:

Выразим отсюда K_max:

Подставляя, получим:

Заданный коэффициент передачи меньше максимального (K<K_max), значит, данная система устойчива.

2. Устойчивость по критерию Гурвица

Для того чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица [2].

Необходимые условия границы устойчивости для системы третьего порядка:

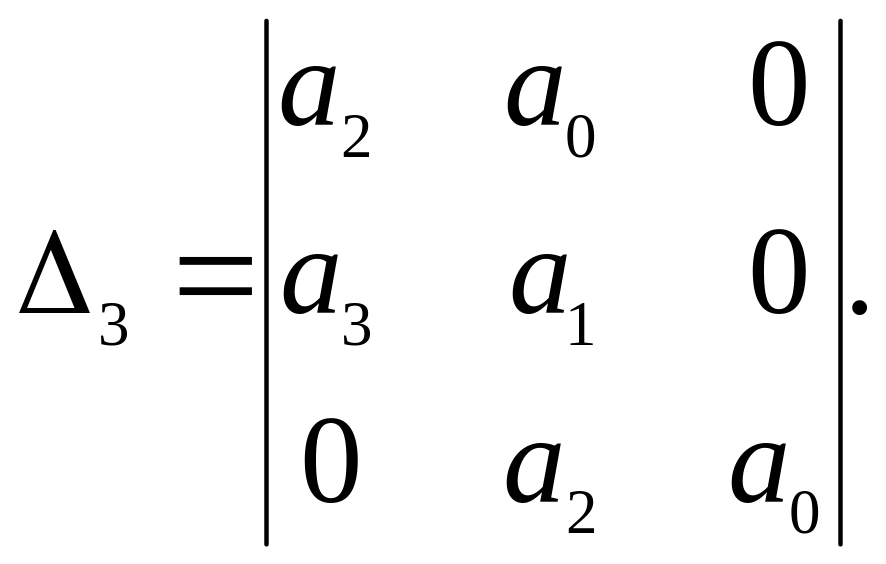
Отсюда следуют условия:

Проверяем:

Все условия критерия Гурвица выполняются, следовательно, система устойчива.

2. Устойчивость по критерию Михайлова

Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от 0 до ∞ начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов комплексной плоскости, не обращаясь в нуль и стремясь к ∞ в n-м квадранте [2].

Условием границы устойчивости является обращение в нуль годографа Михайлова при некотором значении частоты.

Заменим p :

H(jω) =

H(jω) =

Сгруппируем слагаемые с вещественной и мнимой составляющими:

U(ω ) =

V(ω )= (4)

Из выражения (4) выразим :

= .

Найдем значение :

= =

Найденный коэффициент больше заданного, значит, система устойчива. Годограф Михайлова представлен на рисунке 9, по оси абсцисс – реальная часть, по оси ординат действительная часть АФХ.

Рисунок 9 – Годограф Михайлова

Анализ графика, изображенного на рисунке 9, также показывает, что система устойчива. Итак, мы оценили устойчивость данной системы по трем критериям, по каждому из критериев данная система устойчива.