Теоретические вопросы и практические примеры и задачи для аттестации (экзамена) студентов Теоретические вопросы
Напряженное состояние в окрестности точки. Тензор напряжения.
Главные площади и главные напряжения.
Дифференциальные уравнения равновесия.
Двухосное напряженное состояние.
Определение напряжений с помощью круга Мора.
Перемещения и деформации.
Линейные и угловые деформации.
Тензор деформации.
Главные деформации.
Обобщенный закон Гука.
Закон Гука для двухосного напряженного состояния.
Связь между напряжениями и деформациями для анизотропного тела.
Потенциальные усилия при кручении.
Внутренние усилия при кручении.
Напряжения при кручении стержня с круглым поперечным сечением.
Расчет круглых стержней на прочность и жесткость при кручении.
Полная система уравнений теории упругости.
Перемещения и деформации при изгибе балки. Уравнение изгиба балки.
Постановка задач теории упругости в перемещениях.
Постановка задач теории упругости в напряжениях. Функция напряжения.
Перемещения и деформации в пластине при изгибе. Уравнение изгиба пластины.
Напряжения в пластинах при изгибе. Дифференциальные соотношения.
Цилиндрический изгиб пластины.
Чистый изгиб прямоугольных пластин.
Расчет прямоугольных пластин на изгиб с помощью тригонометрических рядов.
Метод конечных разностей в теории упругости.
Метод конечных элементов в теории упругости.
Наибольшие напряжения в пластине. Расчет пластины на прочность.
Дифференциальное уравнение.
Устойчивость тонких пластин.
Практические задачи и примеры
Задача 1
Стержень ступенчато-постоянного сечения находится под действием показанных на рис. 1., а осевых нагрузок. Требуется построить эпюры продольных сил и нормальных напряжений, определить абсолютные удлинения (укорочения) участков стержня и построить эпюру осевых перемещений. В расчетах принять Е = 2 • 104 МПа = 2 • 103 кН/см2.
Задача 2
Стержень ступенчато-постоянного сечения, жестко закрепленный с двух сторон, находится под действием сосредоточенных осевых нагрузок (рис. 1.). Требуется построить эпюры продольных сил, нормальных напряжений и осевых перемещений. В расчетах принять Е = 2 • 105МПа = 2 • 104кН/см2.
Задача 3
Медный стержень ступенчато-постоянного сечения жестко закреплен на левом конце и находится под действием сосредоточенной силы и температурного нагрева на первом участке (рис. 1.). На правом конце имеется зазор δ = 0,01 см между торцом стержня и жесткой опорой. Требуется построить эпюры продольных сил, нормальных напряжений и осевых перемещений. В расчетах принять Е= 1 • 104 кН/см2 = 1 • 105 МПа, α = 1,65 • 10–5 1/град, где α – коэффициент линейного температурного расширения.
Задача 4
Жесткая балка АВ нагружена на конце сосредоточенной силой и поддерживается с помощью стержня CD (рис. 1.). Требуется подобрать сечение стержня в виде двух равнобоких уголков и в виде двух тяг круглого сечения, а также определить величину удлинения стержня и угол поворота балки. Коэффициент надежности по нагрузке принять γf =1,4. Материал стержня — сталь марки ВСт.З. В расчетах принять E=2,1 • 105 МПа = 2,1 • 104 кН/см2, R=210МПа = 21 кН/см2 и γс = 1,0.
Задача 5
Для данной стержневой системы (рис. 1.) требуется определить величину допустимой расчетной силы из условия прочности стержней, величины удлинений стержней и перемещения шарнирного узла В. Материал стержней — сталь марки ВСт.З со следующими характеристиками: Е=2,1 • 105 МПа = 2,1 • 104 кН/см2, R=210МПа=21кН/см2, γс = 1,0.
Для данной стержневой системы (рис. 1.) требуется определить усилия в стержнях DC и ВС и проверить их прочность по методу предельных состояний. Нормативное значение нагрузки qн = 20 кН/м. Коэффициент перегрузки γf = 1,2, R = 210 МПа, γс = 1,0, Е=2,1 • 105 МПа= 2,1 • 104 кН/см2
Задача 7
Короткая стальная труба Ø200×10 мм заполнена бетоном и находится под действием сжимающей силы (рис. 1.). Коэффициент надежности по нагрузке γf = 1,2. Требуется определить продольные силы и напряжения, воспринимаемые стальной трубой и бетоном, и проверить их прочность. Устойчивость колонны и совместную работу трубы и бетона считать обеспеченными. Эффекты, связанные с поперечными деформациями, не учитывать. В расчетах принять:
Ест= 2,1 • 104 кН/см2=2,1 • 105 МПа, Rст=210 МПа,
Еб= 3 • 103 кН/см2=3 • 104 МПа, Rб=210 МПа, γс=1,0.
Задача 8
Для стержневой системы (рис. 1.) требуется: Определить усилия в стержнях СВ и BD, приняв соотношение площадей сечений стержней F2/F1 = 1,2.
Задача 9
На координатных площадках вблизи данной точки тела, находящегося в условиях плоского напряженного состояния, действуют напряжения σх =60 МПа, σу = -20 МПа, τух =τ = -30 МПа.
Направления действия этих напряжений с учетом знаков показаны на рис. 1. для бесконечно малого элемента с координатными площадками. Требуется определить аналитически и графически:
1) Значения главных напряжений и углы наклона главных площадок.
Задача 10
Стальная полоса прямоугольного сечения, имеющая косой сварной шов, находится под действием растягивающих сил Р = 240 кН (рис. 1.).
Требуется определить толщину полосы δ из условий, что в сечении, соответствующем сварному шву, касательные напряжения не превышают [τ] = 80 МПа, а нормальные напряжения — [σ] = 160 МПа.
Задача 11
Жестко закрепленный на одном торце стальной вал сплошного ступенчато-постоянного сечения находится под действием показанных на рис. 1,а скручивающих нагрузок.
Требуется построить эпюру крутящих моментов и определить значения наибольших касательных напряжений на каждом участке вала и углы поворота характерных сечений. В расчетах принять модуль упругости при сдвиге G =0,8 • 105МПа = 0,8 • 104 кН/см2.
Задача 12
Построить эпюры М и Q для консольной балки (рис. 1, а).
Задача 13
Построить эпюры М и Q Для консольной балки (рис. 1, а).
Задача 14
Построить эпюры М и Q для шарнирно-опертой балки (рис. 1, а).
Задача 15
Для шарнирно-оперной балки с консольным участком (рис.1,а ) построить эпюры M и Q.
Задача 16
Для балки с промежуточным шарниром (рис. 1, а) построить эпюры M и Q.
Задача 17
Для
шарнирно-опертой балки, нагруженной
поперечной нагрузкой с интенсивностью
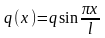(рис.
1, а), требуется построить эпюры
Q
и
М.
Задача 18
Для шарнирно-опертой балки (рис. 1, а) требуется построить эпюры Q и M. На консольном участке балки действует равномерно распределенная моментная нагрузка.
Задача 19
Для шарнирно-опертой балки (рис. 1, а) требуется определить величину параметра k, при котором изгибающие моменты в пролете балки и на опоре В равны по величине и противоположны по знаку.
Задача 20
Для шарнирно-оперной балки (рис. 1, а) требуется определить длину консоли а из условия равенства нулю изгибающего момента в сечении С.
Задача 21
Для шарнирно-опертой балки (рис. 1, а) требуется: Построить эпюры М и Q.
Задача 22
Для деревянной балки прямоугольного сечения (рис. 1, а) требуется: Построить эпюры М и Q.
Задача 23
В стальном двутавре, нагруженном сосредоточенной силой (рис. 1, а), с помощью тензодатчика определена линейная деформация верхних волокон в сечении х= 1,5 м. Требуется определить величину приложенной силы и наибольшие напряжения в двутавровой балке. В расчетах принять εх = ε = -4,6 • 10–4, E=2,1 • 105 МПа = 2,1 • 104 кН/см2.
Задача 24
Для стальной балки коробчатого сечения (рис. 1, а) требуется: Определить величины расчетной и нормативной нагрузок из условия прочности балки, приняв R = 210 МПа, γf = 1,3, γс = 1,0.
Задача 25
Для балочной системы (рис. 1, а) требуется определить величину нагрузки q из условий прочности обеих балок. Материал балок — сталь марки ВСт.З с расчетным сопротивлением R=210 МПа = 21 кН/см2 и γс = 1,0.
